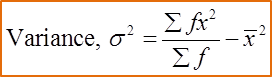Question 7 (2 marks):
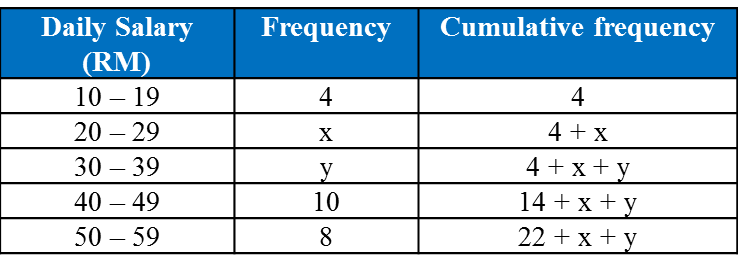
Table shows the information about a set of data.
 Table
Table
State
(a) the value of p if m = 20,
(b) the value of q if p = 2.5.
Solution:
(a)
New standard deviation = original standard deviation × p
20 = 5 × p
p = 4
(b)
New median = [original median × p] + 1
q = 2p × 1
q = 2(2.5) + 1
q = 5 + 1
q = 6
Table shows the information about a set of data.
 Table
Table State
(a) the value of p if m = 20,
(b) the value of q if p = 2.5.
Solution:
(a)
New standard deviation = original standard deviation × p
20 = 5 × p
p = 4
(b)
New median = [original median × p] + 1
q = 2p × 1
q = 2(2.5) + 1
q = 5 + 1
q = 6
Question 8 (3 marks):
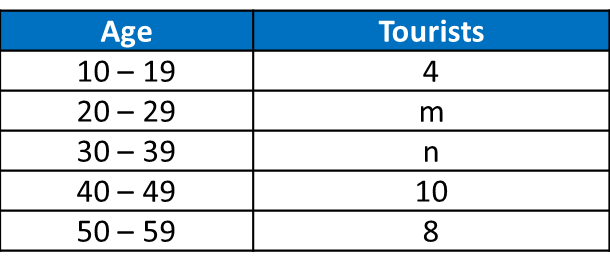
Table shows the distribution of scores obtained by a group of students in a competition.
 Table
Table
(a) State the minimum value of x if the mode score is 4.
(b) Find the mean score of the distribution if x = 1.
Solution:
(a)
Minimum value of x = 8
(b)
Mean=1(3)+2(6)+3(7)+4(1)+5(1)3+6+7+1+1=4518=2.5
Table shows the distribution of scores obtained by a group of students in a competition.
 Table
Table (a) State the minimum value of x if the mode score is 4.
(b) Find the mean score of the distribution if x = 1.
Solution:
(a)
Minimum value of x = 8
(b)
Mean=1(3)+2(6)+3(7)+4(1)+5(1)3+6+7+1+1=4518=2.5
Question 9 (4 marks):
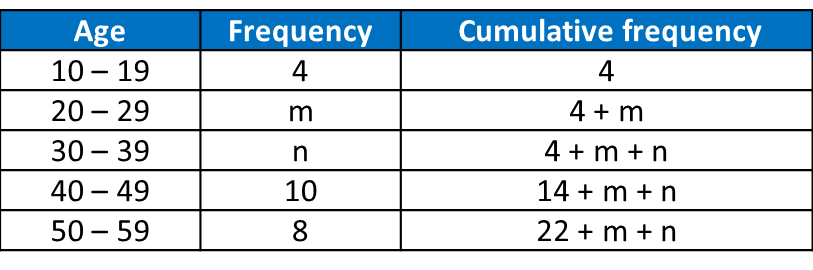
Table shows the distribution of marks for 40 students in an Additional Mathematics test. The number of students for the class interval 40 – 59 is not stated.
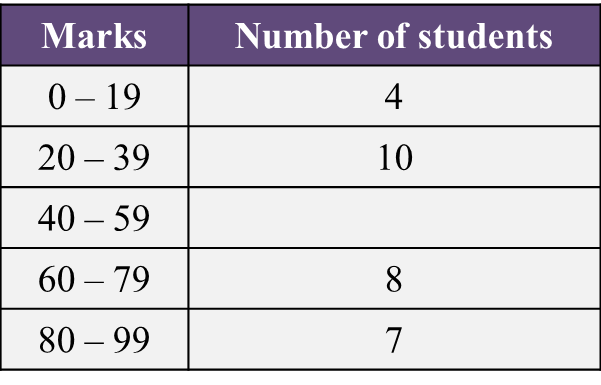 Table
Table
(a) State the modal class.
(b) Puan Zainon, the subject teacher, intends to give a reward to the top ten students. Those students who achieve the minimum mark in the top ten placing will be considered to receive the reward. Elina obtains 74 marks.
Does Elina qualify to be considered to receive the reward? Give your reason.
Solution:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Modal class = 40 – 59
(b)
The top ten placings are T31, T32, T33, ... T40T31=59.5+58(79.5−59.5)=59.5+12.5=72A student has to achieve a minimum markof 72.Elina qualifies for the reward because hermarks > 72 marks.
Table shows the distribution of marks for 40 students in an Additional Mathematics test. The number of students for the class interval 40 – 59 is not stated.
 Table
Table(a) State the modal class.
(b) Puan Zainon, the subject teacher, intends to give a reward to the top ten students. Those students who achieve the minimum mark in the top ten placing will be considered to receive the reward. Elina obtains 74 marks.
Does Elina qualify to be considered to receive the reward? Give your reason.
Solution:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Modal class = 40 – 59
(b)
The top ten placings are T31, T32, T33, ... T40T31=59.5+58(79.5−59.5)=59.5+12.5=72A student has to achieve a minimum markof 72.Elina qualifies for the reward because hermarks > 72 marks.