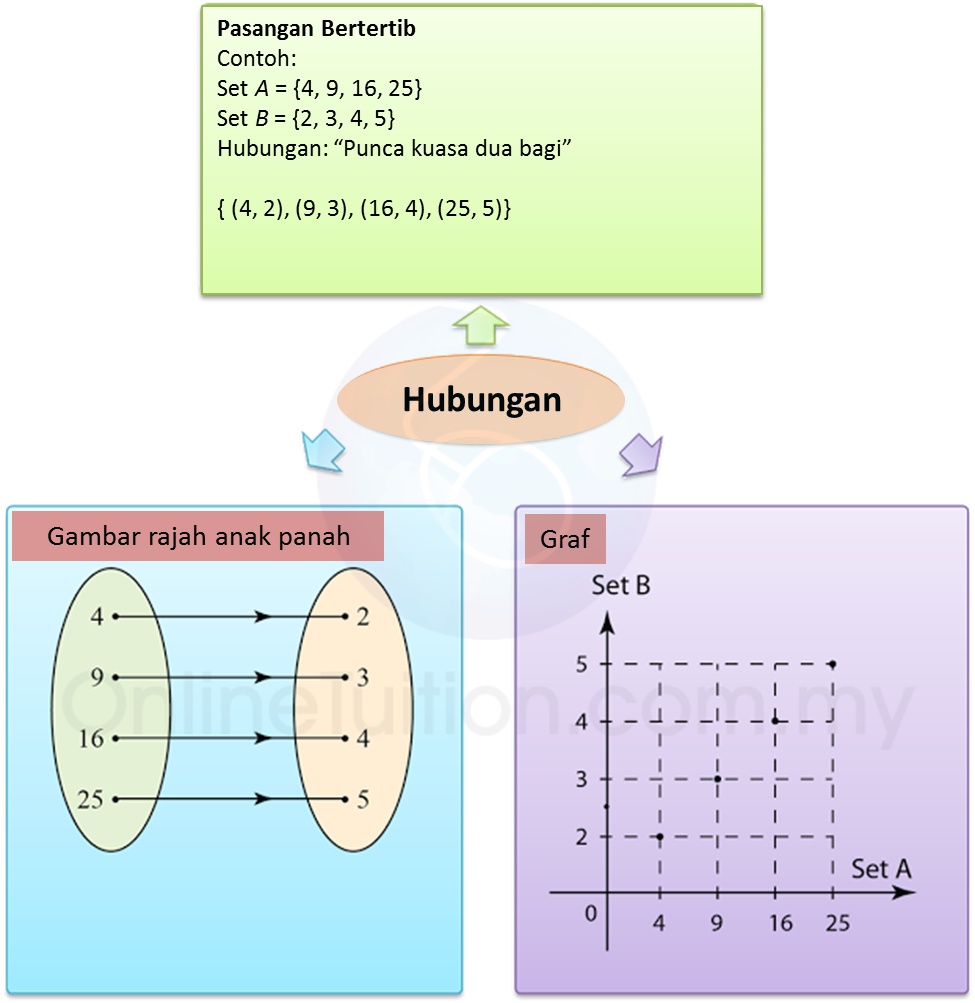
Soalan 22 (3 markah):
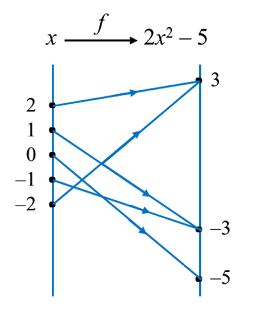
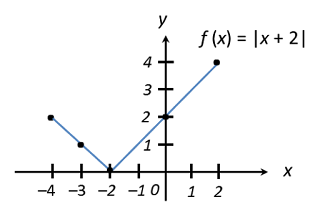
Rajah menunjukkan graf bagi fungsi f : x → |1 – 2x| untuk domain –2 ≤ x ≤ 4.
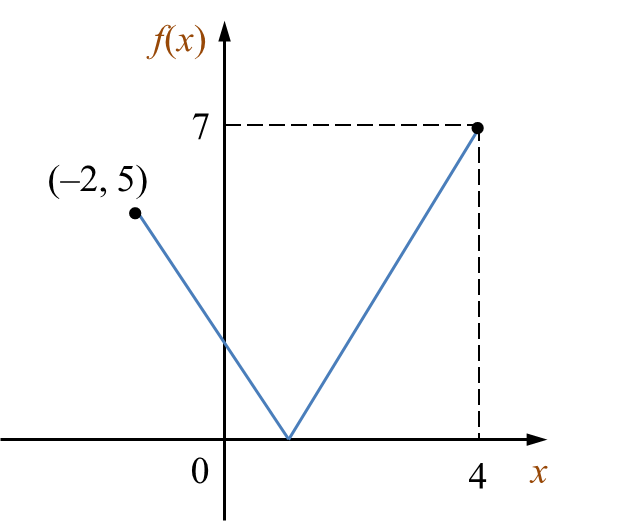 Rajah
Rajah
Nyatakan
(a) objek bagi 7,
(b) imej bagi 3,
(c) domain bagi 0 ≤ f(x) ≤ 5.
Penyelesaian:
(a)
Objek bagi 7 ialah 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
Imej bagi 3 ialah 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Diberi apabila f(x) = 5, x = –2.
Apabila f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Rajah menunjukkan graf bagi fungsi f : x → |1 – 2x| untuk domain –2 ≤ x ≤ 4.
 Rajah
Rajah Nyatakan
(a) objek bagi 7,
(b) imej bagi 3,
(c) domain bagi 0 ≤ f(x) ≤ 5.
Penyelesaian:
(a)
Objek bagi 7 ialah 4.
(b)
f (x) = |1 – 2x|
f (3) = |1 – 2(3)|
= |1 – 6|
= |–5|
= 5
Imej bagi 3 ialah 5.
(c)
|1 – 2x| = 5
1 – 2x = ±5
Diberi apabila f(x) = 5, x = –2.
Apabila f(x) = –5
1 – 2x = –5
2x = 6
x = 3
Domain: –2 ≤ x ≤ 3.
Soalan 23 (4 markah):
Diberi fungsi g : x → 2x – 8, cari
(a) g−1(x),(b) nilai p dengan keadaan g2(3p2)=30.
Penyelesaian:
(a)
Katakan y=g(x)=2x−82x−8=y 2x=y+8 x=y+82Maka, g−1(x)=x+82
(b)
g(x)=2x−8g2(x)=g[g(x)] =g(2x−8) =2(2x−8)−8 =4x−16−8 =4x−24g2(3p2)=304(3p2)−24=306p=54p=9
Diberi fungsi g : x → 2x – 8, cari
(a) g−1(x),(b) nilai p dengan keadaan g2(3p2)=30.
Penyelesaian:
(a)
Katakan y=g(x)=2x−82x−8=y 2x=y+8 x=y+82Maka, g−1(x)=x+82
(b)
g(x)=2x−8g2(x)=g[g(x)] =g(2x−8) =2(2x−8)−8 =4x−16−8 =4x−24g2(3p2)=304(3p2)−24=306p=54p=9


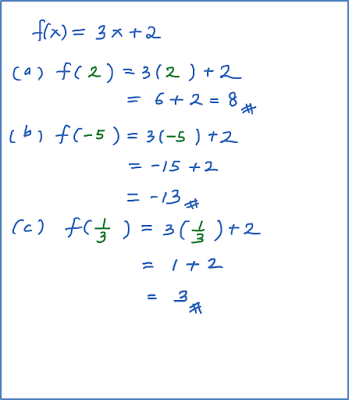

 Rajah
Rajah