Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.5 Rumus bagi sin (A ± B), kos (A ± B), tan (A ± B), sin 2A, kos 2A, tan 2A

Rumus penambahan

\begin{array}{l} • \sin A = 2 \sin \frac{A}{2} k o s \frac{A}{2} \\ • k o s A = \sin^{2} \frac{A}{2} - k o s^{2} \frac{A}{2} \\ k o s A = 2 k o s^{2} \frac{A}{2} - 1 \\ k o s A = 1 - 2 k o s^{2} \frac{A}{2} \\ • \tan A = \frac{2 \tan \frac{A}{2}}{1 - \tan^{2} \frac{A}{2}} \end{array}

5.5.1 Pembuktian Identiti Trigonometri yang Melibatkan Sudut Majmuk dan Sudut Berganda

Contoh 1:

Buktikan setiap identity trigonometri yang berikut.

\begin{array}{l} (a) \frac{s i n (A + B) - s i n (A - B)}{k o s A k o s B} = 2 \tan B \\ (b) \frac{k o s (A + B)}{\sin A k o s B} = k o t A - \tan B \\ (c) \tan (A + 45^{o}) = \frac{\sin A + k o s A}{k o s A - \sin A} \end{array}

penyelesaian:

(a)

\begin{array}{l} (S e b e l a h K i r i) \\ = \frac{s i n (A + B) - s i n (A - B)}{k o s A k o s B} \\ = \frac{(\sin A k o s B + k o s A \sin B) - (\sin A k o s B - k o s A \sin B)}{k o s A k o s B} \\ = \frac{2 k o s A \sin B}{k o s A k o s B} \\ = \frac{2 \sin B}{k o s B} \\ = 2 \tan B = (S e b e l a h K a n a n) \end{array}

(b)

\begin{array}{l} (S e b e l a h K i r i) \\ = \frac{k o s (A + B)}{\sin A k o s B} \\ = \frac{k o s A k o s B - \sin A \sin B}{\sin A k o s B} \\ = \frac{k o s A k o s B}{\sin A k o s B} - \frac{\sin A \sin B}{\sin A k o s B} \\ = \frac{k o s A}{\sin A} - \frac{\sin B}{k o s B} \\ = k o t A - \tan B \\ = (S e b e l a h K a n a n) \end{array}

(c)

\begin{array}{l} (S e b e l a h K i r i) \\ = \tan (A + 45^{o}) \\ = \frac{t a n A + \tan 45^{o}}{1 - t a n A \tan 45^{o}} \\ = \frac{t a n A + 1}{1 - t a n A} \leftarrow \tan 45^{o} = 1 \\ = \frac{\frac{\sin A}{k o s A} + 1}{1 - \frac{\sin A}{k o s A}} \\ = \frac{\sin A + k o s A}{k o s A} \times \frac{k o s A}{k o s A - \sin A} \\ = \frac{\sin A + k o s A}{k o s A - \sin A} \\ = (S e b e l a h K a n a n) \end{array}

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

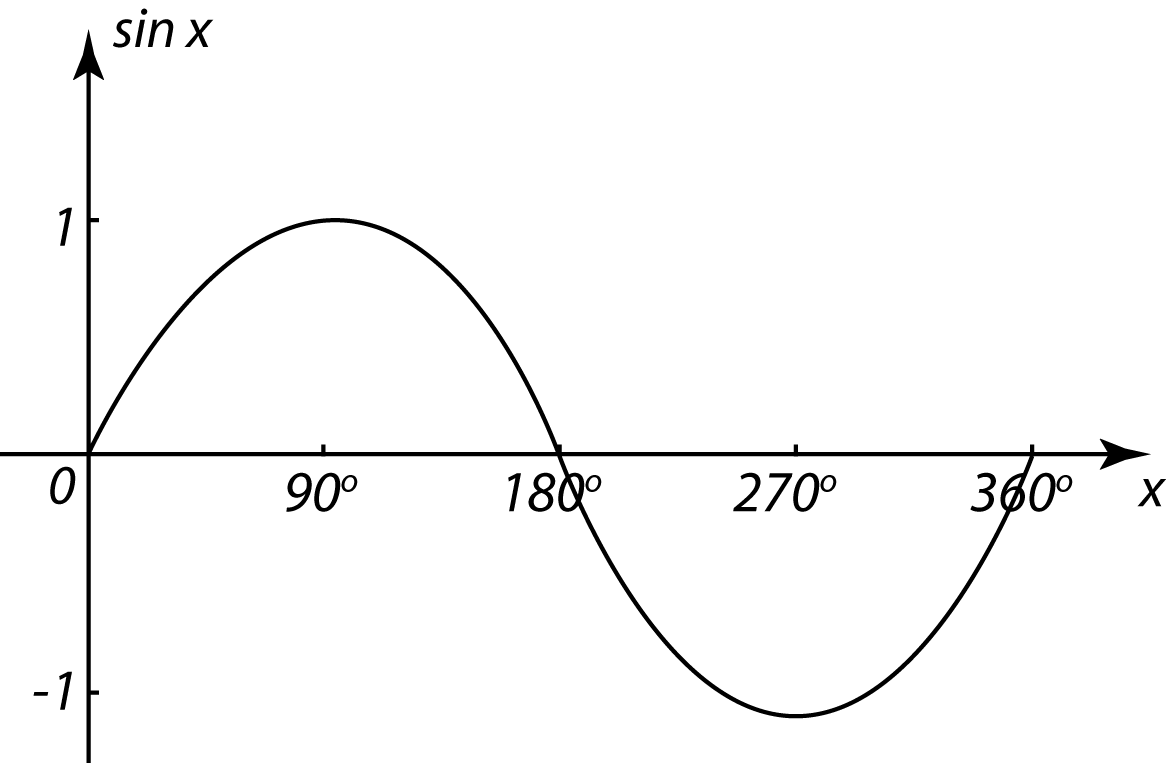
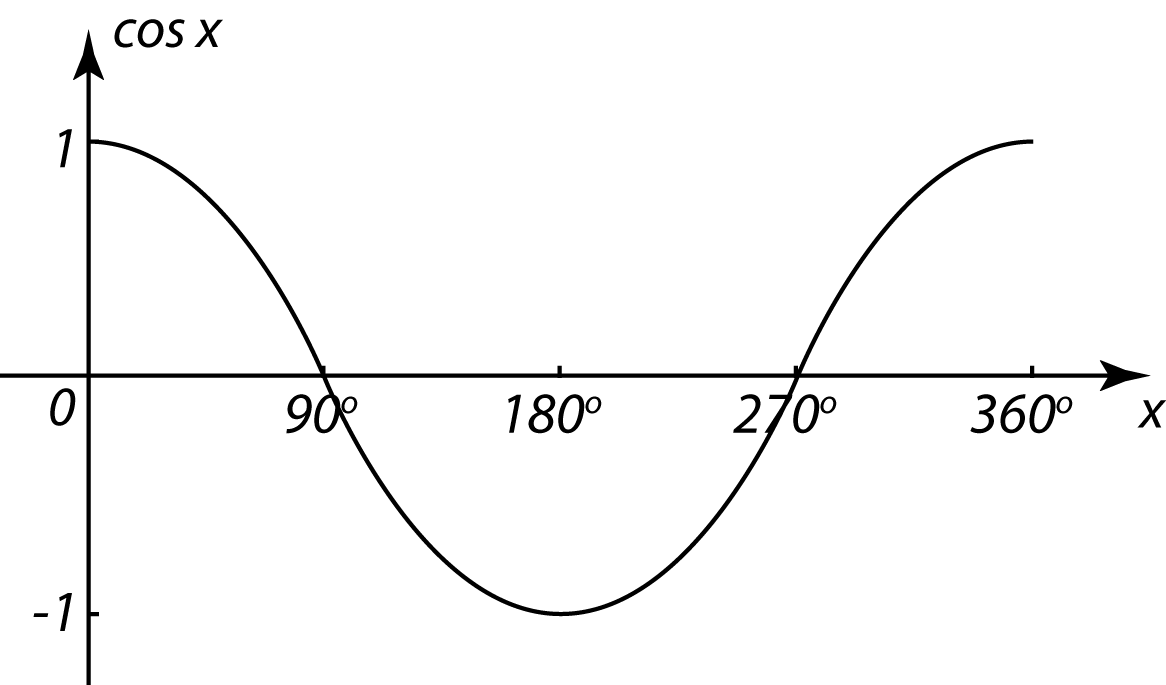
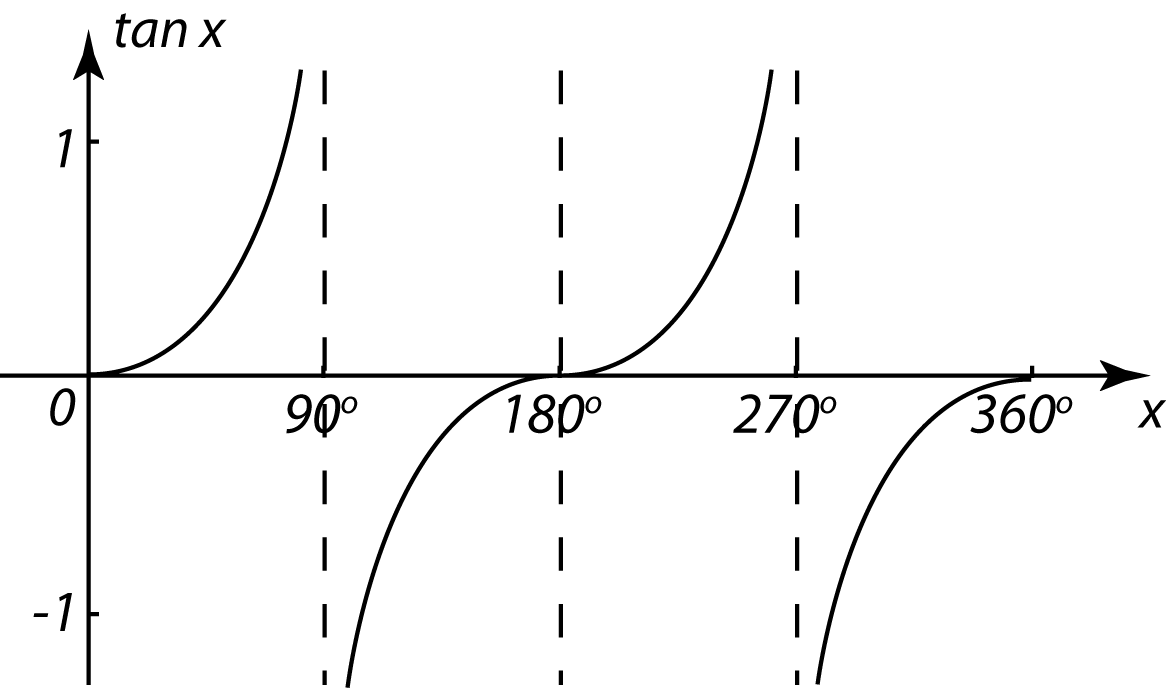5.4 Identiti Asas

sin² x + kos² x = 1

sek² x = 1 + tan² x

kosek² x = 1 + kot² x

Contoh 1 (Pembuktian Identiti Trigonometri dengan Menggunakan Identiti Asas)

Buktikan setiap identity trigonometri yang berikut.

(a) sin²x – kos² x = 1 – 2 kos² x

(b) (1 – kosek²x) (1– sek² x) = 1

Penyelesaian:

(a)

sin²x– kos² x = 1 – 2 kos²x

Sebelah kiri: sin²x– kos² x

= 1 – kos² x – kos² x

= 1 – 2 kos² x (Sebelah kanan)

(b)

(1 – kosek²x) (1– sek² x) = 1

Sebelah kiri: (1 – kosek²x) (1– sek² x)

= (–kot²x) (–tan² x)

= (kot²x) (tan² x)

\begin{array}{l} = (\frac{1}{\tan^{2} x}) \tan^{2} x \\ = 1 (Sebelah kanan) \end{array}

(c)

kot²x – kot² x kos² x = kos² x

Sebelah kiri: kot²x– kot² x kos² x

= kot²x (1 – kos²x)

= kot²x (sin²x)

\begin{array}{l} = \frac{k o s^{2} x}{s i n^{2} x} (s i n^{2} x) \\ = k o s^{2} x (Sebelah kanan) \end{array}

Contoh 2 (Menyelesaikan Persamaan Trigonometri dengan Identiti Asas)

Selesaikan setiap persamaan trigonometri yang berikut untuk 0^o ≤ x ≤ 360^o.

(a) sin²x kos x + 1 = kos x

(b) 2 kosek²x – 5 kot x = 0

Penyelesaian:

(a)

sin²x kos x + 1 = kos x

(1 – kos²x) kos x + 1 = kos x

kos x – kos³x + 1 = kos x

kos³x = 1

kos x = 1

x = 0^o, 360^o

(b)

2 kosek²x – 5 kot x = 0

2 (1 + kot²x) – 5 kot x = 0

2 + 2 kot²x – 5 kot x = 0

2 kot²x – 5 kot x + 2 = 0

(2 kotx – 1) (kot x – 2) = 0

kotx = ½ atau kot x = 2

kotx = ½ atau kotx = 2

tan x = 2, tan x = ½

x =63.43^o, 243.43^o , x = 26.57^o, 206.57^o

(Perhatian: tangen adalah positif dalam sukuan I dan III)

Oleh itu, x = 26.57^o, 63.43^o, 206.57^o, 243.43^o

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.3.2c Melakar Graf Fungsi Trigonometri (Bahagian 3)

Contoh 2:

(a) Lakar graf bagi y = –½ kos x untuk 0 ≤ x ≤ 2π.

(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu graf yang sesuai untuk mencari bilangan penyelesaian bagi persamaan

\frac{π}{2 x} + k o s x = 0

untuk 0 ≤ x ≤ 2π.

Nyatakan bilangan penyelesaian itu.

Penyelesaian:

(a)

(b)

\begin{array}{l} \frac{π}{2 x} + k o s x = 0 \\ \frac{π}{2 x} = - k o s x \\ \frac{π}{4 x} = - \frac{1}{2} k o s x \leftarrow \begin{array}{l} darab kedua-dua \\ belah dengan \frac{1}{2} \end{array} \\ y = \frac{π}{4 x} \leftarrow y = - \frac{1}{2} k o s x \end{array}

Graf yang sesuai ialah

y = \frac{π}{4 x} .

x	$\frac{π}{2}$	π	2π
$y = \frac{π}{4 x}$	½	¼	⅛

Daripada graf, terdapat 2 titik persilangan untuk 0 ≤ x ≤ 2π.

Maka, terdapat 2 penyelesaian bagi persamaan $\frac{π}{2 x} + k o s x = 0.$

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.3.2a Melakar Graf Fungsi Trigonometri (Bahagian 1)

Contoh:

Lakarkan graf bagi setiap fungsi trigonometri yang berikut untuk 0 ≤ x ≤ 2π.

(a) y = 3 sin x
(b) y = 2 kos x

(e) y = sin 2x
(f) y = kos 2x

Penyelesaian:

(a) y = 3 sin x

(b) y = 2 kos x

(c) y = sin x + 1

(d) y = kos x –1

(e) y = sin 2x

(f) y = kos 2x

Bab 16 Fungsi Trigonometri

Posted on June 14, 2016 by user

5.3.1 Graf fungsi Sinus, Kosinus, dan Tangen

(a) Graf y = sin x, 0^o ≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
sin	0	1	0	-1	0

(b) Graf y = kos x, 0^o ≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
kos x	1	0	-1	0	1

(c) Graf y = tan x, 0^o ≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
tan x	0	∞	0	∞	0