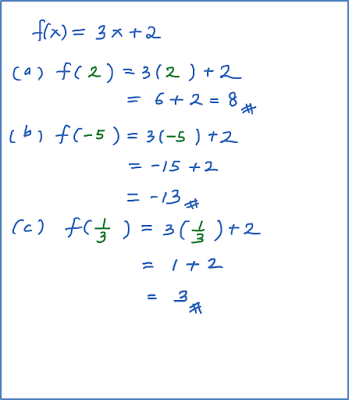1.6 Fungsi, SPM Praktis (Soalan Panjang)
Soalan 1:
Fungsi f dan g ditakrifkan sebagai f
: x → x– 1 dan .
Cari
(a) nilai gf(3),
(b) nilai fg(-1 ),
(c) fungsi gubahanfg,
(d) fungsi gubahangf,
(e) fungsi gubahang 2 ,
(f) fungsi gubahanf 2 .
(a) nilai gf(3),
(b) nilai fg(-1 ),
(c) fungsi gubahanfg,
(d) fungsi gubahangf,
(e) fungsi gubahang 2 ,
(f) fungsi gubahanf 2 .
Penyelesaian:

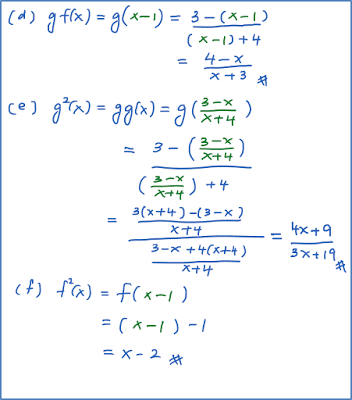
Soalan 2:
Diberi f
: x → hx + k dan f2 : x → 4x + 15.
(a)
Cari nilai hdan k.
(b)
Ambil nilai h> 0, cari nilai-nilai x di mana f (x2) = 7x
Penyelesaian:
(a)
Langkah 1: cari f2 (x)
Diberi f (x) = hx + k
f2 (x) = ff (x) = f (hx + k)
= h (hx + k) + k
= h2x + hk + k
Langkah 2: bandingkan dengan f2(x) yang diberi
f2 (x) = 4x + 15
h2x
+ hk+ k = 4x + 15
h2 = 4
h = ± 2
Apabila, h = 2
hk + k = 15
2k + k = 15
k = 5
Apabila, h = –2
hk + k = 15
–2k + k = 15
k = –15
(b)
h > 0, h
= 2, k = 5
Diberi f (
x) = hx +
k
f (x) = 2x + 5
f (x2) = 7x
2 (x2) + 5 = 7x
2x2 – 7x+ 5 = 0
(2x – 5)(x–1
) = 0
2x – 5 = 0 atau x –1=
0
x = 5/2
x = 1