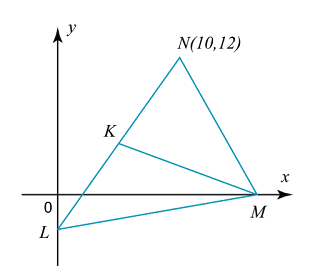
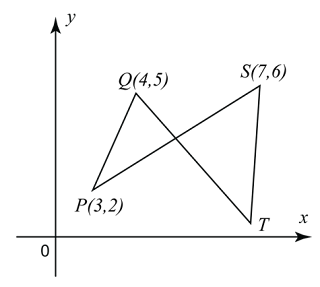Soalan 9 (3 markah):
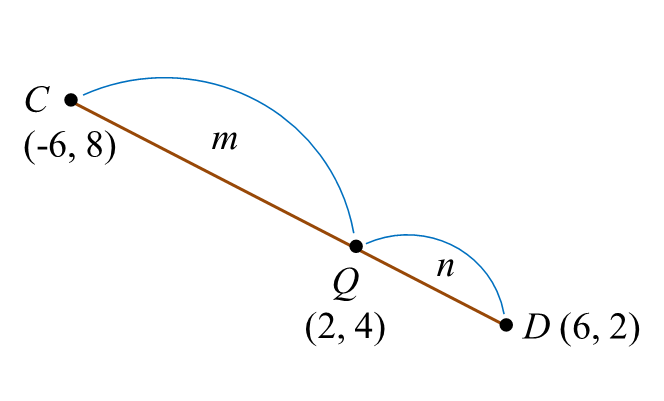
Satu garis lurus melalui P(3, 1) dan Q(12, 7). Titik R membahagi tembereng garis PQ dengan keadaan 2PQ = 3RQ.
Cari koordinat R.
Penyelesaian:
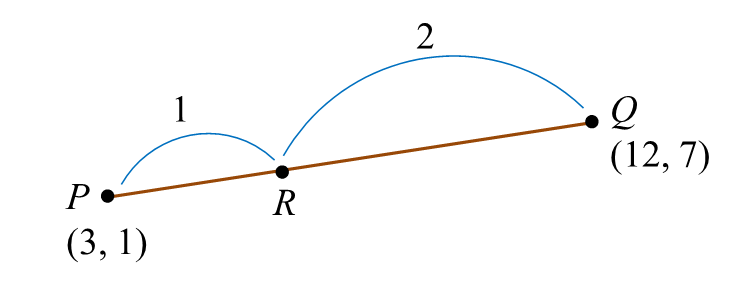
2PQ=3RQPQRQ=32Titik R=(1(12)+2(3)1+2,1(7)+2(1)1+2)=(183,93)=(6,3)
Satu garis lurus melalui P(3, 1) dan Q(12, 7). Titik R membahagi tembereng garis PQ dengan keadaan 2PQ = 3RQ.
Cari koordinat R.
Penyelesaian:

2PQ=3RQPQRQ=32Titik R=(1(12)+2(3)1+2,1(7)+2(1)1+2)=(183,93)=(6,3)
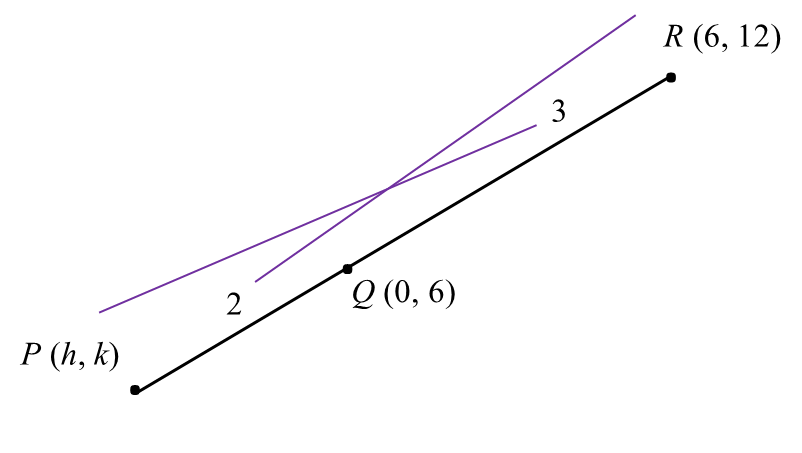
Soalan 10 (3 markah):
Maklumat berikut adalah merujuk kepada persamaan dua garis lurus, AB dan CD.
AB:y−2kx−3=0 CD:x3h+y4=1 dengan keadaan h dan k ialah pemalar.
Diberi garis lurus AB dan garis lurus CD adalah berserenjang antara satu sama lain, ungkapkan h dalam sebutan k.
Penyelesaian:
AB:y−2kx−3=0y=2kx+3mAB=2kCD:x3h+y4=1mCD=−43hmAB×mCD=−12k×(−43h)=−1−8k=−3hh=83k
Maklumat berikut adalah merujuk kepada persamaan dua garis lurus, AB dan CD.
AB:y−2kx−3=0 CD:x3h+y4=1 dengan keadaan h dan k ialah pemalar.
Diberi garis lurus AB dan garis lurus CD adalah berserenjang antara satu sama lain, ungkapkan h dalam sebutan k.
Penyelesaian:
AB:y−2kx−3=0y=2kx+3mAB=2kCD:x3h+y4=1mCD=−43hmAB×mCD=−12k×(−43h)=−1−8k=−3hh=83k
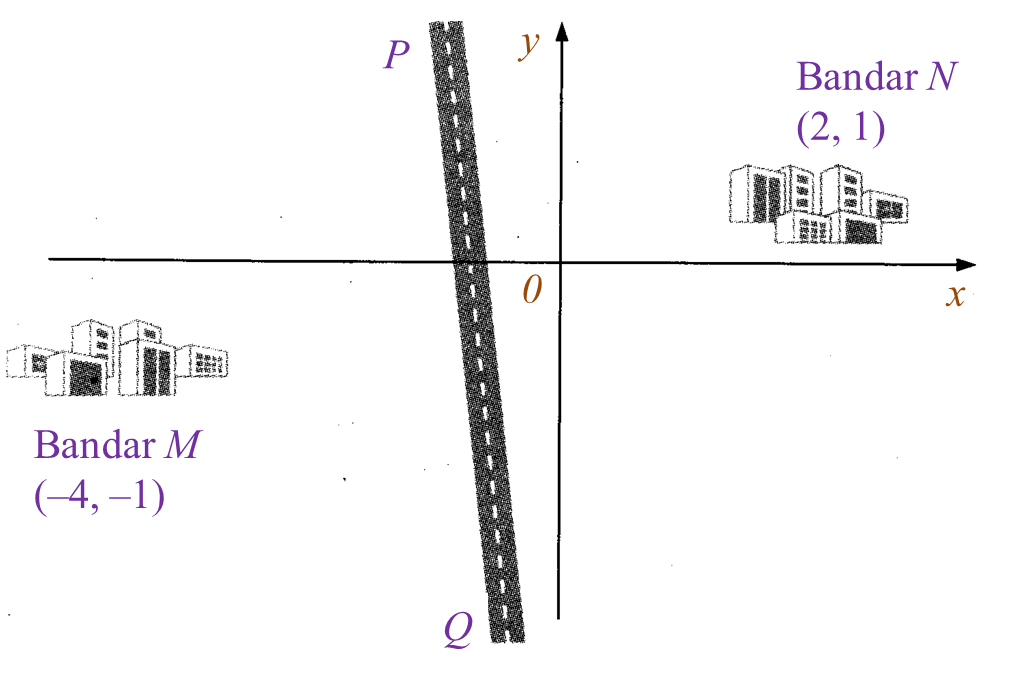
 Rajah 1
Rajah 1