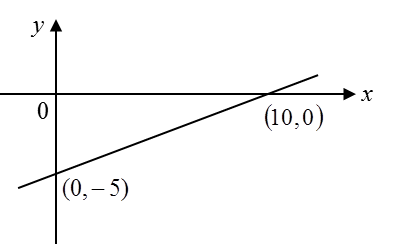6.8 Geometri Koordinat, SPM Praktis (Kertas 2)
Soalan 2:

Rajah menunjukkan trapezium PQRS. Diberi persamaan PQialah 2y – x – 5 = 0, cari
(a)
nilai w,
(b)
persamaan PS dan seterusnya cari koordinat P,
(c)
lokus M supaya segitiga QMS adalah sentiasa berserenjang di M.
Penyelesaian:
(a)
Persamaan PQ,
2y – x – 5 = 0
2y = x + 5
y=12x+52∴(b)
Titik S = (4, –3), m = –2
y – y1 = m (x– x1)
y – (–3) = –2 (x – 4)
y + 3 = –2x + 8
y = –2x + 5
Persamaan PS ialah y = –2x + 5
PS is y = –2x + 5-----(1)
PQ is 2y = x + 5-----(2)
Gantikan (1) ke dalam (2)
2 (–2x + 5) = x + 5
–4x + 10 = x + 5
–5x = –5
x = 1
Dari (1), y = –2(1) + 5
y = 3
Koordinat titik P = (1, 3).
(c)
Katakan M = (x, y)
Diberi ∆QMS berserenjang di M
Oleh itu, ∆QMS = 90o
(mQM) (mMS) = –1
(y – 5) (y + 3) = –1(x– 5) (x – 4)
y2 + 3y – 5y – 15 = –1(x2 – 4x – 5x + 20)
y2 – 2y – 15 = –x2 + 9x – 20
x2 + y2– 9x – 2y + 5 = 0
Jadi, persamaan lokus titik M ialah
x2 + y2 – 9x – 2y + 5 = 0.