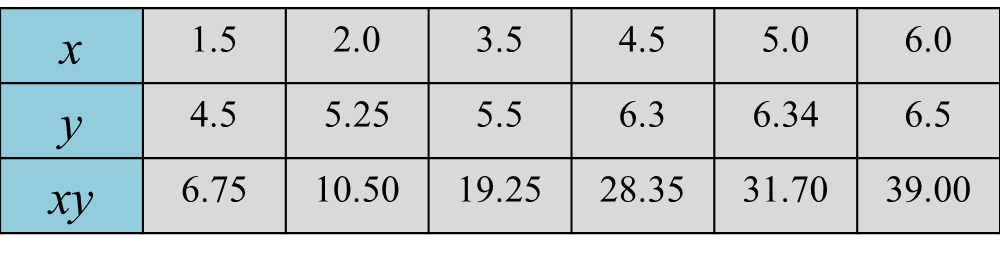
Soalan 8 (3 markah):
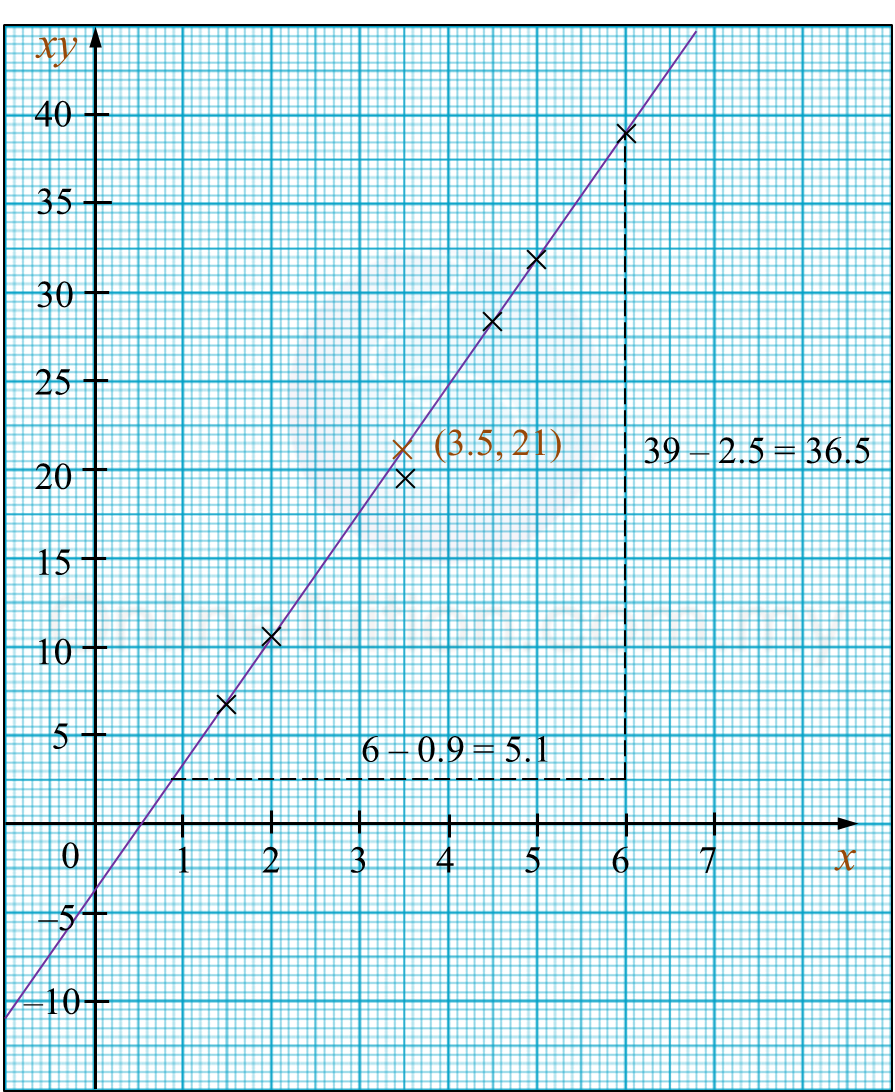
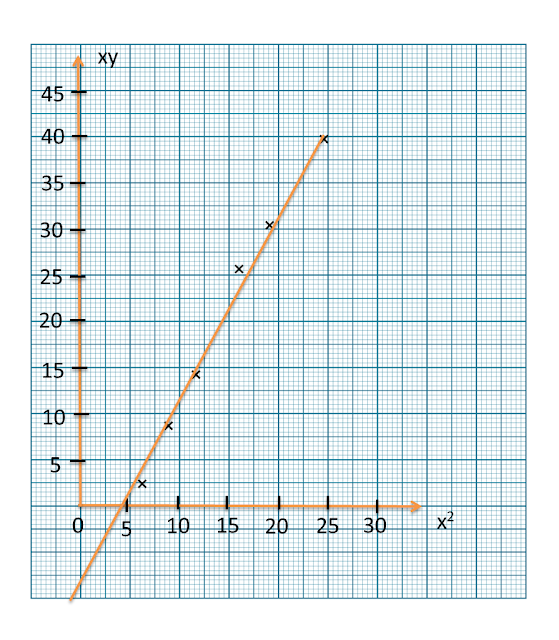
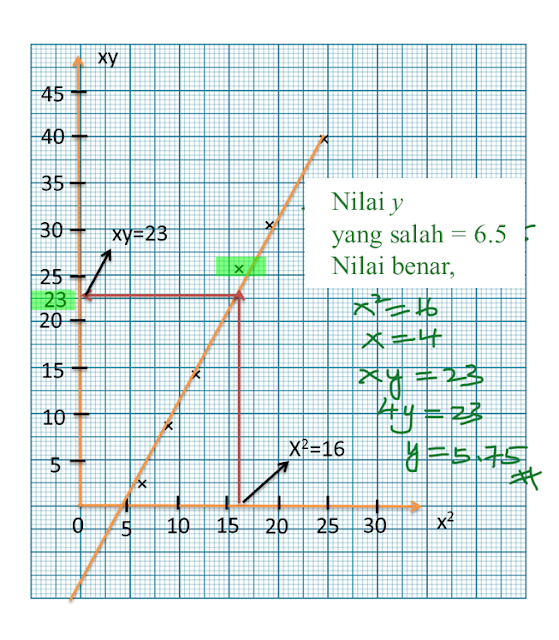
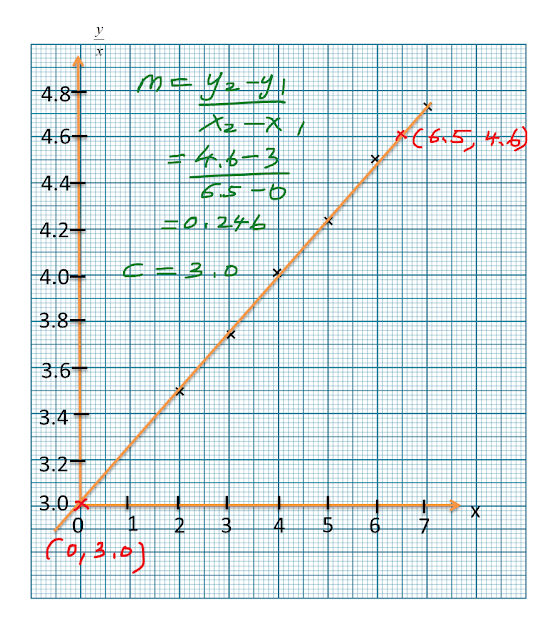
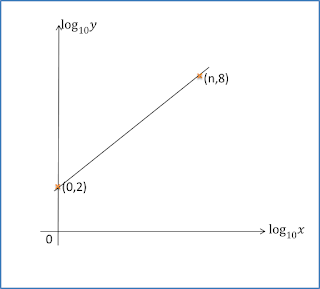
Rajah menunjukkan graf garis lurus x2y melawan 1x.
 Rajah
Rajah
Berdasarkan Rajah, ungkapkan y dalam sebutan x.
Penyelesaian:
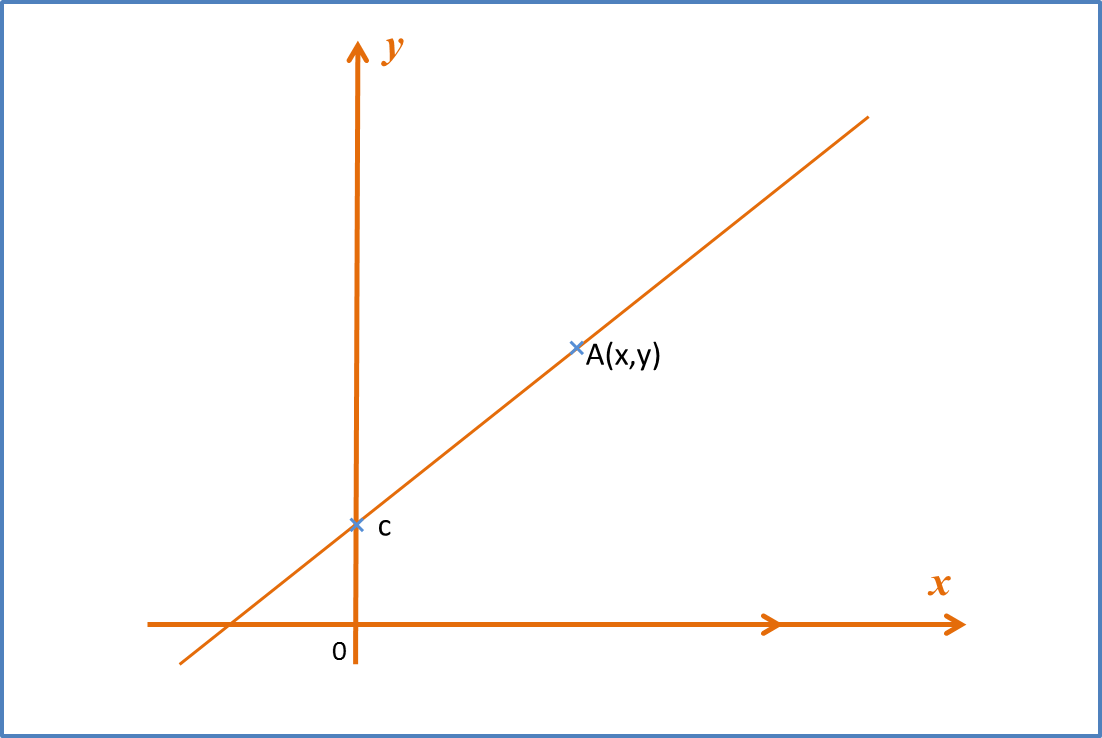
m=4−(−5)6−0=32c=−5Y=x2y, X=1xY=mX+cx2y=32(1x)+(−5)x2y=32x−5x2y=3−10x2xyx2=2x3−10xy=2x33−10x
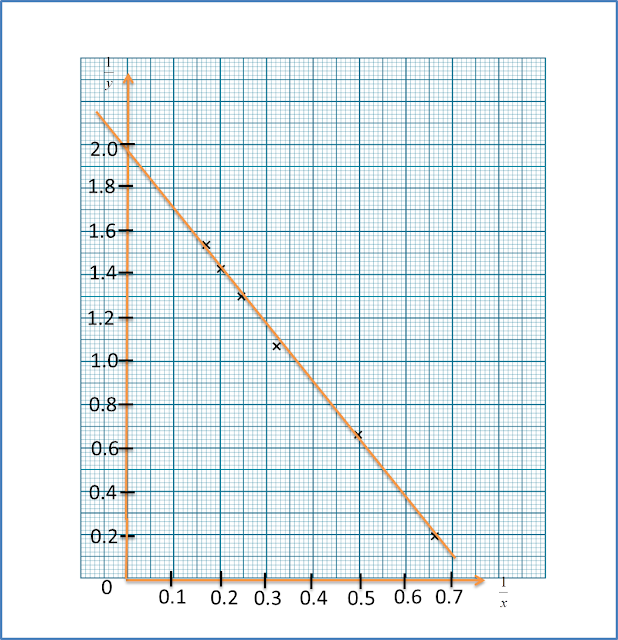
Rajah menunjukkan graf garis lurus x2y melawan 1x.
 Rajah
RajahBerdasarkan Rajah, ungkapkan y dalam sebutan x.
Penyelesaian:
m=4−(−5)6−0=32c=−5Y=x2y, X=1xY=mX+cx2y=32(1x)+(−5)x2y=32x−5x2y=3−10x2xyx2=2x3−10xy=2x33−10x
Soalan 9 (3 markah):
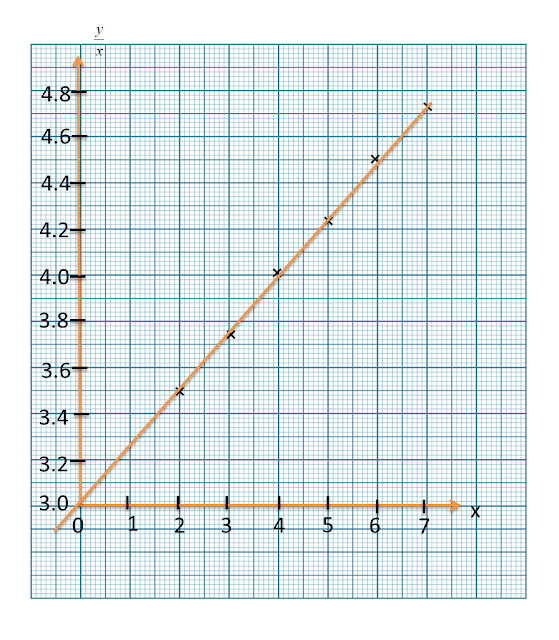
Pembolehubah x dan y dihubungkan oleh persamaan y=x+rx2 , dengan keadaan r ialah pemalar. Rajah menunjukkan graf garis lurus yang diperoleh dengan memplotkan (y−x) melawan 1x2.
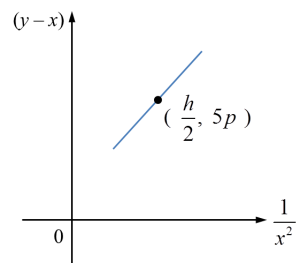 Rajah
Rajah
Ungkapkan h dalam sebutan p dan r.
Penyelesaian:
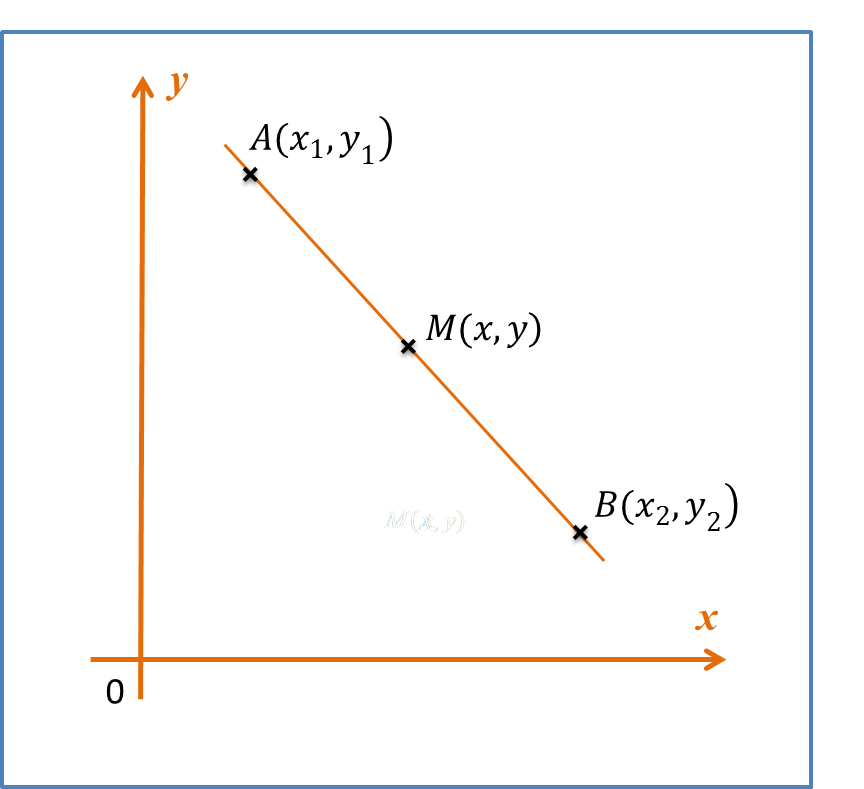
y=x+rx2y−x=r(1x2)+0Y=mX+cm=r, c=0m=y2−y1x2−x1r=5p−0h2−0hr2=5phr=10ph=10pr
Pembolehubah x dan y dihubungkan oleh persamaan y=x+rx2 , dengan keadaan r ialah pemalar. Rajah menunjukkan graf garis lurus yang diperoleh dengan memplotkan (y−x) melawan 1x2.
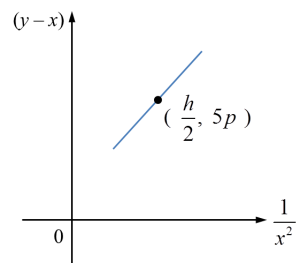 Rajah
RajahUngkapkan h dalam sebutan p dan r.
Penyelesaian:
y=x+rx2y−x=r(1x2)+0Y=mX+cm=r, c=0m=y2−y1x2−x1r=5p−0h2−0hr2=5phr=10ph=10pr