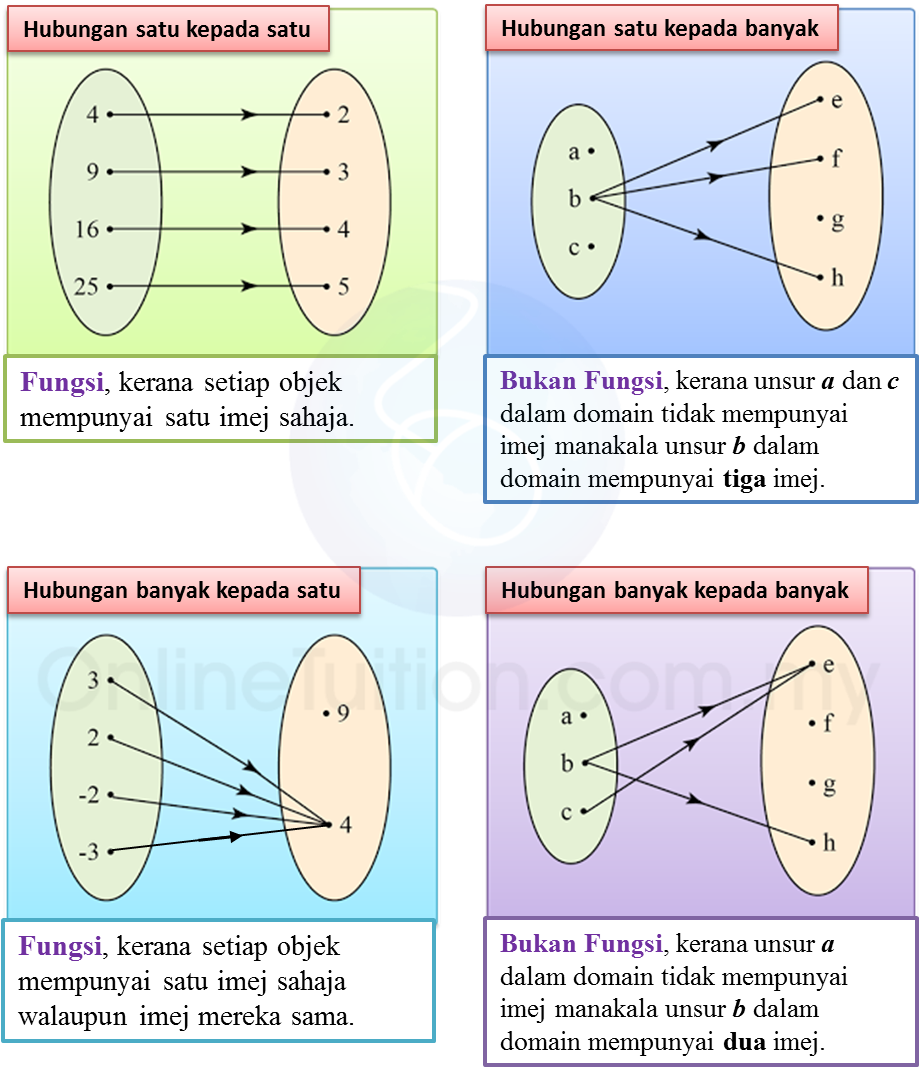
1.2.2
Fungsi
(C) Domain, Kodomain, Objek, Imej, dan Julat bagi Suatu Fungsi
Contoh 3:
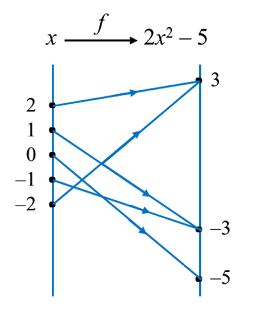
Gambar rajah anak panah di atas mewakili satu fungsi
f : x → 2
x2 – 5. Nyatakan
(a)
domain,
(b)
julat,
(c)
imej bagi –2,
(d)
objek bagi,
(i)
–3,
(ii)
–5.
Penyelesaian:
(a)
Domain = {–2, –1, 0, 1, 2}.
(b)
Julat = {–5, –3, 3}.
(c)
Imej bagi –2 ialah 3.
(d)
(i) Objek bagi –3 ialah 1 dan –1.
(ii)
Objek bagi –5 ialah 0.
(D)
Fungsi Nilai Mutlak
1.
Tanda | | menandakan nilai mutlak bagi suatu nombor. Secara amnya, nilai mutlak bagi nombor x, iaitu | x|, ditakrifkan seperti berikut.
2.
Ini bermakna tanda bagi suatu nilai mutlak sentiasa positif.
3.
| x |
dibaca sebagai modulus bagi x.
4.
Nilai mutlak bagi fungsi f(
x) ialah nilai berangka bagi f(x) dan ditandakan sebagai | f(x)|.
Contoh 4:
Diberi fungsi f: x → |x + 2|.
(a)
Cari imej bagi –4, –3, 0, dan 2.
(b)
Lakarkan graf bagi f (x) bagi domain –4 ≤ x ≤ 2.
Seterusnya, nyatakan nilai julat f (x) berdasarkan domain yang diberi.
Penyelesaian:
(a)
Diberi f (x) = |x + 2|
Imej bagi –4 ialah f(–4) = | –4 + 2| = | –2| = 2
Imej bagi –3 ialah f(–3) = | –3 + 2| = | –1| = 1
Imej bagi 0 ialah f(0) = | 0 + 2| = | 2 | = 2
Imej bagi 2 ialah f(2) = | 2 + 2| = | 4 | = 4
(b)
Daripada (a),
f(–4) = 2
f(–3) = 1
f(0) = 2
f(2) = 4
Tentukan titik supaya graf menyentuh paksi-x.
Pada paksi-x,f (x) = 0
|x + 2| = 0
x+ 2 = 0
x= –2
Oleh itu, julat bagi nilai f (x) ialah 0 ≤ f(x) ≤ 4.

 Rajah
Rajah