Bab 5 Indeks dan Logaritma

Posted on October 15, 2016 by user

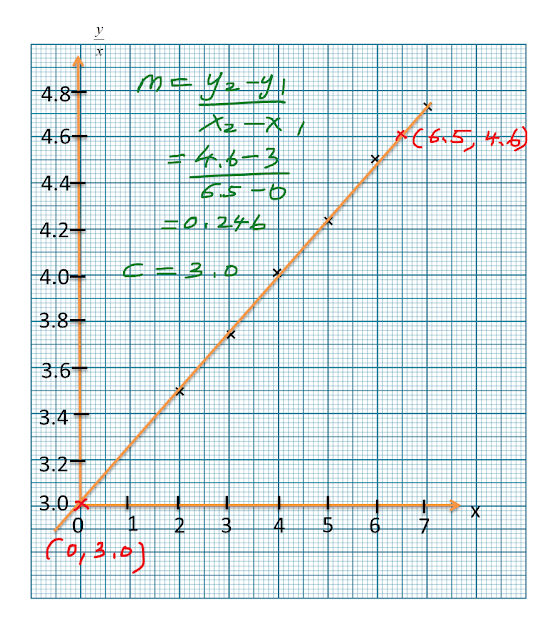
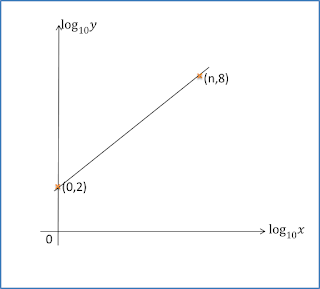
5.6 Indeks dan Logaritma, SPM Praktis (Soalan Panjang)

Soalan 3:

Diberi bahawa p= 3^r dan q = 3^t, ungkapkan yang berikut dalam sebutan rdan/ atau t.

$(a) \log_{3} \frac{p q^{2}}{27},$

(b) log₉p – log₂₇ q.

Penyelesaian:

(a)

Diberi p = 3^r, log₃ p = r

q= 3^t, log₃ q =t

$\log_{3} \frac{p q^{2}}{27}$

= log₃ pq² – log₃27

= log₃ p + log₃ q² – log₃ 3³

= r + 2 log₃ q – 3 log₃ 3

= r + 2 log₃ q – 3(1)

= r + 2t – 3

(b)

log₉ p– log₂₇ q

$\begin{array}{l} = \frac{\log_{3} p}{\log_{3} 9} - \frac{\log_{3} q}{\log_{3} 27} \\ = \frac{r}{\log_{3} 3^{2}} - \frac{t}{\log_{3} 3^{3}} \\ = \frac{r}{2 \log_{3} 3} - \frac{t}{3 \log_{3} 3} \\ = \frac{r}{2} - \frac{t}{3} \end{array}$

Soalan 4:

(a) Permudahkan:

log₂(2x + 1) – 5 log₄ x²+ 4 log₂ x

(b) Seterusnya, selesaikan persamaan:

log₂(2x + 1) – 5 log₄ x²+ 4 log₂ x= 4

Penyelesaian:

(a)

log₂ (2x + 1) – 5 log₄ x²+ 4 log₂ x

$\begin{array}{l} = \log_{2} (2 x + 1) - \frac{5 \log_{2} x^{2}}{\log_{2} 4} + 4 \log_{2} x \\ = \log_{2} (2 x + 1) - \frac{5}{2} \log_{2} x^{2} + \log_{2} x^{4} \\ = \log_{2} (2 x + 1) - \log_{2} {(x^{2})}^{(\frac{5}{2})} + \log_{2} x^{4} \end{array}$

$\begin{array}{l} = \log_{2} (2 x + 1) - \log_{2} x^{5} + \log_{2} x^{4} \\ = \log_{2} \frac{(2 x + 1) (x^{4})}{x^{5}} \\ = \log_{2} \frac{2 x + 1}{x} \end{array}$

(b)

log₂ (2x + 1) – 5 log₄ x²+ 4 log₂ x= 4

$\begin{array}{l} \log_{2} \frac{2 x + 1}{x} = 4 \\ \frac{2 x + 1}{x} = 2^{4} \\ \frac{2 x + 1}{x} = 16 \\ 2 x + 1 = 16 x \\ 14 x = 1 \\ x = \frac{1}{14} \end{array}$

Bab 4 Persamaan Serentak

Posted on October 10, 2016 by user

4.2 SPM Praktis, Persamaan Serentak, (Soalan panjang)

Soalan 5:

Selesaikan persamaan serentak.

5y – 6x= 2

$\frac{4 y}{x} - \frac{3 x}{y} = 4.$

Penyelesaian:

5y – 6x= 2 ----- (1)

$\begin{array}{l} \frac{4 y}{x} - \frac{3 x}{y} = 4 ------- (2) \\ Daripada (1), \\ y = \frac{2 + 6 x}{5} ------- (3) \end{array}$

Gantikan (3) dalam (2),

$\begin{array}{l} \frac{4 (\frac{2 + 6 x}{5})}{x} - \frac{3 x}{(\frac{2 + 6 x}{5})} = 4 \\ \frac{8 + 24 x}{5 x} - \frac{15 x}{2 + 6 x} = 4 \\ \frac{(8 + 24 x) (2 + 6 x) - (15 x) (5 x)}{5 x (2 + 6 x)} = 4 \end{array}$

16 + 48x + 48x + 144x² – 75x² = 20x (2 + 6x)

69x² + 96x + 16 = 40x + 120x²

51x² – 56x – 16 = 0

(3x – 4)(17x + 4) = 0

3x – 4 = 0 atau 17x + 4 = 0

$x = \frac{4}{3} atau x = - \frac{4}{17}$

$\begin{array}{l} Gantikan x = \frac{4}{3} dalam persamaan (3), \\ y = \frac{2 + 6 (\frac{4}{3})}{5} = 2 \end{array}$

$\begin{array}{l} Gantikan x = - \frac{4}{17} dalam persamaan (3), \\ y = \frac{2 + 6 (- \frac{4}{17})}{5} = \frac{2}{17} \end{array}$

$Maka penyelesaian ialah (\frac{4}{3}, 2) dan (- \frac{4}{17}, \frac{2}{17}) .$

Soalan 6:
Selesaikan persamaan serentak.

$\begin{array}{l} x + 2 y = 1 \\ 2 x^{2} + y^{2} + x y = 5 \end{array}$
Beri jawapan anda betul kepada tiga tempat perpuluhan.

Penyelesaian:

$\begin{array}{l} x + 2 y = 1.......... (1) \\ 2 x^{2} + y^{2} + x y = 5.......... (2) \\ x = 1 - 2 y .......... (3) \\ Gantikan (3) ke dalam (2), \\ 2 {(1 - 2 y)}^{2} + y^{2} + (1 - 2 y) y = 5 \\ 2 (1 - 4 y + 4 y^{2}) + y^{2} + y - 2 y^{2} = 5 \\ 2 - 8 y + 8 y^{2} - y^{2} + y - 5 = 0 \\ 7 y^{2} - 7 y - 3 = 0 \\ a = 7, b = - 7, c = - 3 \\ x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ y = \frac{- (- 7) \pm \sqrt{{(- 7)}^{2} - 4 (7) (- 3)}}{2 (7)} \\ y = \frac{7 \pm \sqrt{133}}{14} \\ y = 1.324 atau - 0.324 \\ Dari x = 1 - 2 y \\ Apabila y = 1.324, \\ x = 1 - 2 (1.324) = 1.648 \\ Apabila y = - 0.324, \\ x = 1 - 2 (- 0.324) = 1.648 \\ ∴ Penyelesaian ialah (1.648, 1.324) dan (1.648, - 0.324) . \end{array}$

Bab 2 Persamaan Kuadratik

Posted on October 10, 2016 by user

2.3d Pembentukan Persamaan Kuadratik Baru daripada Persamaan Kuadratik yang diberi (Contoh Soalan)

Contoh:

Dineri punca-punca bagi x ² – 3x – 7 = 0 ialah αdan β, cari persamaan yang mempunyai punca-punca α² β dan α β².

Penyelesaian:

Bahagian 1 : Cari HTP dan HDP bagi persamaan kuadratik yang diberi

x ² – 3x – 7 = 0

a = 1, b = –3, c = –7

HTP: α + β→ (α, β ialah punca-punca persamaan kuadratik ax ² + bx + c = 0)

$\begin{array}{l} = - \frac{b}{a} \\ = - (\frac{- 3}{1}) = 3 \end{array}$

$\begin{array}{l} HDP : α β = \frac{c}{a} \\ = \frac{- 7}{1} = - 7 \end{array}$

Bahagian 2 : Bentukkan persamaan kuadratik baru dengan mencari HTP dan HDP

Persamaan kuadratik baru mempunyai punca-punca α² β dan α β²

HTP = α² β + α β²

= αβ (α + β)

= –7 (3) = –21 → (Daripada bahagian 1, α + β = 3, αβ = –7)

HDP = α² β (α β²)

= α³β³= (α β)³

= (–7)³ = –343

Untuk membentuk persamaan kuadratik baru,

x ² – (HTP)x + HDP = 0

x ² – (–21)x + (–343) = 0

x ² + 21 x –343 = 0

Maka, persamaan yang mempunyai punca-punca α² β dan α β² ialah,

x ² + 21 x –343 = 0

Bab 2 Persamaan Kuadratik

Posted on October 10, 2016 by user

2.1.2 Punca Persamaan Kuadratik

Punca persamaan kuadratik ialah nilai bagi pembolehubah yang memuaskan persamaan kuadratik itu.

Contoh 1:
Tentukan sama ada 1, 2, dan 3 ialah punca-punca bagi persamaan kuadratik x² − 5x + 6 = 0.

Penyelesaian:

Apabila x = 1,
x² − 5x + 6 = 0

(1)²− 5(1) + 6 = 0

2 = 0 ← (tidak sama nilai di kedua-dua belah)

x = 1 bukan punca persamaan itu

Apabila x= 2,
x² − 5x + 6 = 0

(2)²− 5(2) + 6 = 0

0 = 0 ← (sama nilai di kedua-dua belah)

x = 2 ialah punca persamaan itu.

Apabila x= 3
x² − 5x + 6 = 0

(3)²− 5(3) + 6 = 0

0 = 0 ← (sama nilai di kedua-dua belah)

x = 3 ialah punca persamaan itu.

Kesimpulan:
1. 2 dan 3 memuaskan persamaan x² − 5x + 6 = 0, maka ia adalah punca-punca bagi persamaan itu.

2. 1 tidak memuaskan persamaan x² − 5x + 6 = 0, maka ia bukan punca-punca bagi persamaan itu.

Contoh 2 (Punca yang memuaskan suatu persamaan):

Peringatan: Punca persamaan kuadratik ialah nilai bagi pembolehubah yang memuaskan persamaan kuadratik itu.
(a) Diberi x= 3 adalah punca bagi persamaan kuadratik x ² + 2x + p = 0, cari nilai p.
(b) Punca-punca bagi persamaan kuadratik 3x ² + hx + k = 0 ialah −2 dan 4. Cari nilai h dan nilai k.

Penyelesaian:

(a)

x ² + 2x + p = 0

3²+ 2(3) + p = 0 → ganti x = 3 (punca persamaan)

p = –15

(b)

3x ² + hx + k = 0

x = − 2 dan 4 ialah punca-punca persamaan,

3 (− 2)²+ h (−2) + k = 0 → ambil x = −2

12 – 2h+ k = 0

2h – k = 12 ------ (1)

3 (4 )²+ h (4) + k = 0 → ambil x = 4

48 + 4h + k = 0

4h + k= –48 ----- (2)

(1) + (2),

6h = –36

h = –6

2 (–6) – k= 12

k = –24

Bab 13 Hukum Linear

Posted on October 9, 2016 by user

2.7 Hukum Linear, SPM Praktis (Kertas 2)

Soalan 3:

Gunakan kertas graf untuk menjawap soalan ini.

Jadual di bawah menunjukkan nilai-nilai bagi dua pemboleh ubah x dan y, yang diperoleh daripada satu eksperimen. Pemboleh ubah x dan y dihubungkan oleh persamaan

$y = q x + \frac{p}{q x}$ , dengan keadaan p dan q ialah pemalar.

x	2.5	3.0	3.5	4.0	4.5	5.0
y	1.0	2.7	4.1	6.5	6.8	8.0

Salah satu daripada nilai y salah direkodkan.

(a) Berdasarkan jadual di atas, bina satu jadual bagi nilai-nilai x² dan xy.

(b) plot xy melawan x² dengan menggunakan skala 2 cm kepada 5 unit pada kedua-dua paksi.

Seterusnya, lukis garis lurus penyuaian terbaik.

(i) Nyatakan nilai y yang salah direkodkan dan tentukan nilai sebenarnya.

(ii) Cari nilai p dan nilai q.

Penyelesaian:

(a)

(b)

(c)(i)

(c)(ii)

Bab 13 Hukum Linear

Posted on October 9, 2016 by user

2.7 Hukum Linear, SPM Praktis (Kertas 2)

Soalan 2:

Gunakan kertas graf untuk menjawap soalan ini.

Jadual di bawah menunjukkan nilai-nilai bagi dua pemboleh ubah x dan y, yang diperoleh daripada satu eksperimen. Pemboleh ubah x dan y dihubungkan oleh persamaan

$\frac{a}{y} = \frac{b}{x} + 1$ , dengan keadaan k dan p ialah pemalar.

x	1.5	2	3	4	5	6
y	5.004	1.540	0.930	0.770	0.705	0.656

(a) Berdasarkan jadual di atas, bina satu jadual bagi nilai-nilai

$\frac{1}{x} dan \frac{1}{y} .$

(b) plot

$\frac{1}{y} melawan \frac{1}{x},$ dengan menggunakan skala 2 cm kepada 0.1 unit pada paksi

$\frac{1}{x}$ dan skala 2 cm kepada 0.2 unit pada paksi

$\frac{1}{y}$ ,

Seterusnya, lukis garis lurus penyuaian terbaik.

(i) a,

(ii) b,

Penyelesaian:

(a)

(b)

(c)(i)(ii)

Bab 13 Hukum Linear

Posted on October 9, 2016 by user

2.7 Hukum Linear, SPM Praktis (Kertas 2)

Soalan 1:

Gunakan kertas graf untuk menjawap soalan ini.

Jadual di bawah menunjukkan nilai-nilai bagi dua pemboleh ubah x dan y, yang dihubungkan oleh persamaan

$y = 5 h x^{2} + \frac{k}{h} x$ , dengan keadaan h dan k ialah pemalar.

x	2	3	4	5	6	7
y	7.0	11.3	16.0	21.2	27.1	33.2

(a) Dengan menggunakan skala 2 cm kepada 1 unit pada paksi-x dan skala 2 cm kepada 0.2 unit pada paksi

$\frac{y}{x}$ , plot graf

$\frac{y}{x}$ melawan x.

Seterusnya, lukis garis lurus penyuaian terbaik.

(b) Gunakan graf di (a) untuk mencari nilai

(i) h,

(ii) k,

(iii) yapabila x = 6.

Penyelesaian:

(a)

Sediakan satu jadual yang memberikan nilai X (x) dan nilai Y

$(\frac{y}{x}) .$

(b)

Cari kecerunan garis lurus penyuaian terbaik, m, dan pintasan-Y daripada graf.

(b)(i)(ii)

~ Tukar fungsi tak linear kepada bentuk linear melalui persamaan Y = mX + c.

~ Bandingkan dengan nilai-nilai m dan c di graf, cari nilai h dan nilai k.

(b)(iii)

Nilai yapabila x = 6

Bab 13 Hukum Linear

Posted on October 8, 2016 by user

2.5 Memperoleh Maklumat daripada Graf Garis Lurus Penyuaian Terbaik

Contoh 1:

Gunakan kertas graf untuk menjawap soalan ini.

Jadual di bawah menunjukkan nilai-nilai bagi dua pemboleh ubah x dan y, yang dihubungkan oleh persamaan y = pk^√x dengan keadaan p dan k ialah pemalar.

x	1	4	9	16	25	36
y	1.80	2.70	4.05	6.08	9.11	13.67

(a) Plotkan log₁₀y melawan √x. Seterusnya, lukiskan garis lurus penyuaian terbaik.

(b) Gunakan graf anda dari (a) untuk mencari nilai pdan nilai k.

Penyelesaian:

(a)

Langkah 1: Sediakan suatu jadual yang memberikan nilai X (√x) dan nilai Y (log₁₀y).

Langkah 2: Dengan menggunakan skala yang sesuai, lukis garis lurus penyuaian terbaik dengan memplot graf Y (log₁₀y) melawan X (√x).

(b)

Langkah 3: Cari kecerunan garis lurus penyuaian terbaik, m, dan pintasan-Y daripada graf.

Langkah 4: Tukar fungsi tak linear kepada bentuk linear melalui persamaan Y = mX + c.

Langkah 5: Bandingkan dengan nilai-nilai m dan c di langkah 3, cari nilai p dan nilai k.

Bab 13 Hukum Linear

Posted on October 7, 2016 by user

2.6 Hukum Linear, SPM Praktis (Kertas 1)

Soalan 6:

Dua pembolehubah, x dan y, dihubungkan oleh persamaan y² = px^q. Apabila graf lgy melawan lgx diplotkan, graf garis lurus yang diperoleh mempunyai kecerunan –2 dan pintasan tegak ialah 0.5. Cari nilai p dan nilai q.

Penyelesaian:

Soalan 7:

Dua pembolehubah, x dan y, dihubungkan oleh persamaan

$y = \frac{c}{d - x} .$ Apabila graf y melawan xy diplotkan, graf garis lurus yang diperoleh mempunyai kecerunan 2.5 dan pintasan paksi-y ialah 1.25. Cari nilai cdan nilai d.

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 7, 2016 by user

2.6 Hukum Linear, SPM Praktis (Kertas 1)

Soalan 4:

Dua pembolehubah, x dan y, dihubung oleh rumus y = px³, dengan pialah pemalar. Cari nilai p dan nilai n.

Penyelesaian:

Soalan 5:

Rajah A menunjukkkan sebahagian daripada lengkung y = ax² + bx. Rajah B menunjukkkan sebahagian daripada garis lurus yang diperoleh apabila y= ax² + bx ditukar kepada bentuk linear. Cari

(a) nilai a dan nilai b,

(b) nilai p dan nilai q.

Rajah A

Rajah B

Penyelesaian: