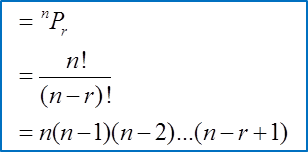Bab 13 Hukum Linear

Posted on October 6, 2016 by user

2.6 Hukum Linear, SPM Praktis (Kertas 1)

Soalan 1:

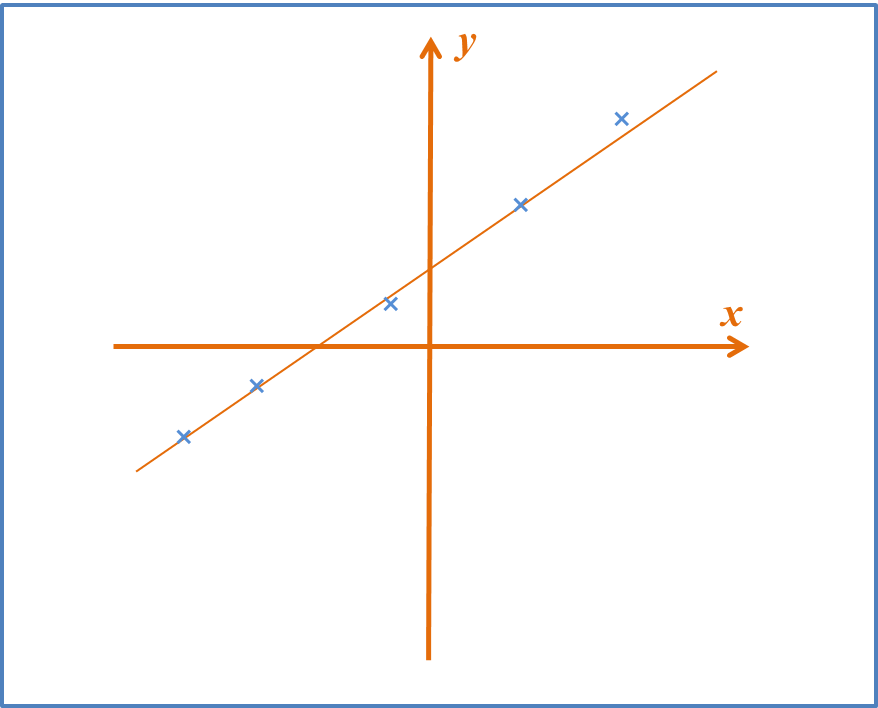
Rajah di bawah menunjukkkan sebahagian daripada graf garis lurus diperoleh apabila √y melawan x².

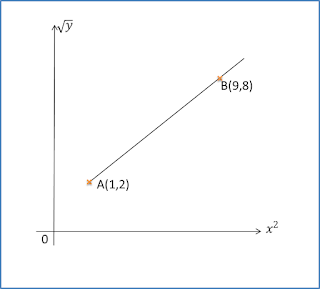
Ungkapkan ydalam sebutan x.

Penyelesaian:

Soalan 2:

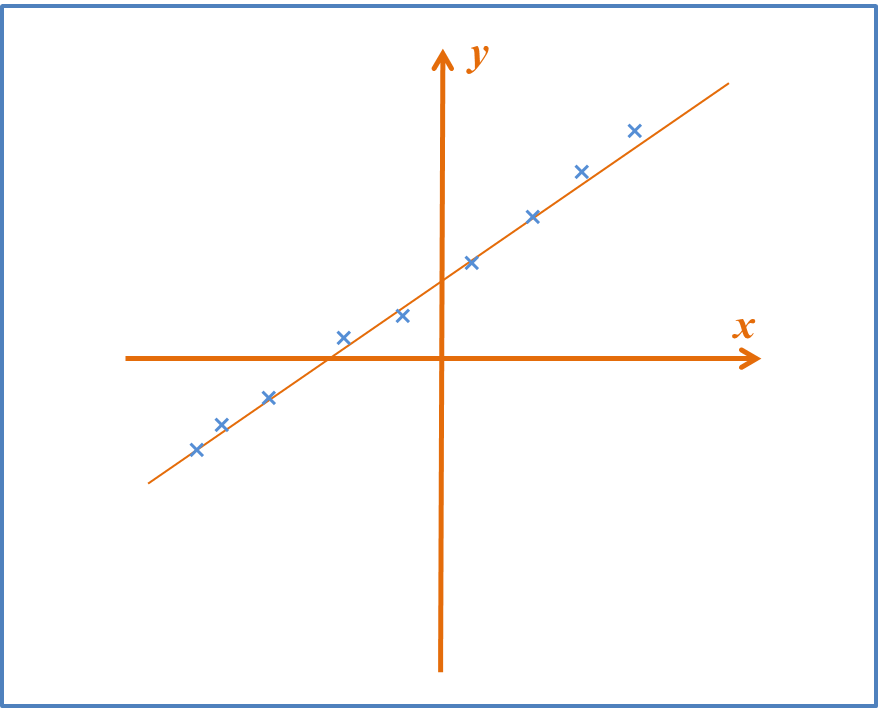
Rajah di bawah menunjukkkan sebahagian daripada graf garis lurus diperoleh apabila

\frac{y}{x} melawan \sqrt{x} .

Diberi persamaan tak linear yang asal ialah

y = p x + q x^{\frac{3}{2}}

, hitungkan nilai p dan nilai q.

Penyelesaian:

Soalan 3:

Rajah di bawah menunjukkkan graf garis lurus yang dihubungkan oleh persamaan

\frac{x}{y} = \frac{2}{x} + 3 x .

Cari nilai pdan nilai k.

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 6, 2016 by user

2.4 Menentukan Nilai Pemalar Bagi Persamaan Tak Linear

Contoh 1:

Tukarkan hubungan tak linear y = pxⁿ^-1, dengan keadaan k dan n adalah pemalar kepada persamaan linear. Nyatakan kecerunan dan pintasan pada paksi-y.

Penyelesaian:

Contoh 2:

Rajah di bawah menunjukkan graf garis lurus yang diperoleh dengan memplot y²melawan √x.

(a) Cari persamaan garis lurus penyuaian terbaik.

(b) Tentukan nilai bagi

(i) x apabila y = 4

(ii) y apabila x = 25.

Penyelesaian:

Contoh 3:

Pembolehubah x dan y dihubungkan oleh persamaan

y = \frac{P}{3^{x}}

dengan ksebagai pemalar.

Rajah di bawah menunjukkan garis lurus yang diperoleh dengan memplotkan log₁₀y melawan x.

(a) Ungkapkan persamaan

y = \frac{P}{3^{x}}

dalam bentuk linear yang digunakan untuk memperoleh garis lurus di atas.

(b) Cari nilai p.

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 5, 2016 by user

2.2 Penggunaan Hukum Linear Kepada Fungsi Tak Linear

Menukar persamaan Tak Linear kepada Bentuk Linear

1. Suatu fungsi tak linear yang melibatkan pembolehubah x dan y boleh ditukarkan kepada bentuk linear melalui persamaan Y = mX + c, dengan X dan Y ialah fungsi x dan y masing-masing atau kedua-duanya.

2. Bagi hubungan tak linear, graf yang diperoleh apabila y diplotkan melawan x merupakan satu lengkung.

3. Untuk mendapatkan satu graf garis lurus, langkah-langkah yang berikut boleh diambil.

(i) Tukar persamaan tak linear kepada bentuk linear Y = mX + c.
Misalnya:
Persamaan tak linear;

y = a x + \frac{b}{x}

, a, b pemalar, ditukar kepada bentuk linear:
xy = a (x²) + b
dengan Y = xy , m =a, X = x² dan c = b

(ii) Dengan menggunakan skala yang sesuai, plot graf Y (xy) melawan X (x²), maka satu graf garis lurus diperoleh.

4. Pemalar-pemalar a dan b boleh ditentukan daripada kecerunan dan pintasan-Y graf garis lurus yang diperoleh. Bagi contoh di atas;

a = kecerunan garis lurus

b = pintasan-Y

Bab 13 Hukum Linear

Posted on October 5, 2016 by user

2.1.1 Melukis Garis Lurus Penyuaian Terbaik

Langkah-langkah untuk Melukis Garis Lurus Penyuaian Terbaik

(i) Memilih skala yang sesuai bagi paksi-x dan paksi-y, pastikan titik-titik diplot dengan tepat dan graf yang dihasilkan adalah cukup besar pada sehelai kertas graf.

(ii) Menanda titik-titik dengan betul.

(iii) Guna sebuah pembaris panjang dan telus untuk melukis garis lurus penyuaian terbaik.

Langkah 1: Memilih skala yang sesuai bagi paksi-x dan paksi-y

(graf yang dihasilkan adalah melebihi 50% sehelai kertas graf)

Langkah 2: Menanda titik-titik dengan betul

Langkah 3: Melukis garis lurus penyuaian terbaik

Perhatian:

- Garis lurus itu menyambungkan 4 titik

- Satu titik berada di atas garis lurus

- Satu titik berada di bawah garis lurus

Bab 13 Hukum Linear

Posted on October 4, 2016 by user

2.3.3 Penggunaan Hukum Linear Kepada Fungsi Tak Linear (Contoh)

Contoh 3:

Tukarkan setiap hubungan tak linear yang berikut kepada bentuk linear Y = mX + c.
Nyatakan kecerunan graf dan pintasan-Y dalam bentuk a dan b.

(a) y = ab^x

(b) y = ax^b

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 4, 2016 by user

2.3.2 Penggunaan Hukum Linear Kepada Fungsi Tak Linear (Contoh)

Contoh 2:

Tukarkan setiap hubungan tak linear yang berikut kepada bentuk linear Y = mX + c. Nyatakan kecerunan graf dan pintasan-Y dalam bentuk a dan b.

(a) kx² + ty² = x

\begin{array}{l} (b) y = \frac{x}{p + q x} \\ (c) h y = x + \frac{k}{x} \end{array}

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 4, 2016 by user

2.3.1 Penggunaan Hukum Linear Kepada Fungsi Tak Linear (Contoh)

Contoh 1:

Tukarkan setiap hubungan tak linear yang berikut kepada bentuk linear Y = mX + c. Nyatakan kecerunan graf dan pintasan-Ydalam bentuk a dan b.

(a) y = ax³ + bx²

(b)

y = a x + \frac{b}{x}

\begin{array}{l} (d) x y = \frac{p}{x} + q x \\ (e) y = a \sqrt{x} + \frac{b}{\sqrt{x}} \\ (f) \frac{a}{y} = \frac{b}{x} + 1 \end{array}

Penyelesaian:

Bab 13 Hukum Linear

Posted on October 4, 2016 by user

2.1 Garis Lurus Penyuaian Terbaik

Garis lurus penyuaian terbaik mempunyai ciri-ciri yang berikut:

(a) ia menyambungkan kebanyakan titik yang diplotkan pada graf,

(b) titik-titik yang tidak terletak pada garis lurus penyuaian terbaik itu bertaburan secara seimbang di kedua-dua belah garis lurus itu.

Contoh:

Tentukan sama ada graf-graf di bawah mempunyai ciri-ciri garis lurus penyuaian terbaik.

(a)

Ya! Ini adalah garis lurus penyuaian terbaik. Garis lurus itu menyambungkan 3 titik, dan 2 titik yang tidak terletak pada garis lurus penyuaian terbaik itu bertaburan secara seimbang di kedua-dua belah garis lurus itu.

(b)

Tidak! Ini bukan garis lurus penyuaian terbaik. Garis lurus itu mempunyai titik-titik yang lebih banyak di sebelah atas garis lurus berbanding dengan sebelah bawah garis.

Tambahan pula, titik yang tidak terletak pada garis lurus penyuaian terbaik itu TIDAK bertaburan secara seimbang di kedua-dua belah garis lurus itu.

Bab 17 Pilir Atur dan Gabungan

Posted on October 3, 2016 by user

6.1.2 Pilir Atur (Bahagian 2)

(C) Pilih Atur r Benda daripada n Benda

Jika n benda yang berlainan hendak disusun pada satu baris dengan melibatkan r benda pada sesuatu ketika, maka bilangan susunan atau pilihatur yang boleh dilakukan ialah,

Contoh 1:

Menilai setiap yang berikut:

{(a)}^{5} P_{2} {(b)}^{7} P_{3} {(c)}^{9} P_{4}

Penyelesaian:

\begin{array}{l} (a) \\ ^{5} P_{2} = \frac{5!}{(5 - 2)!} = \frac{5!}{3!} \\ = \frac{5 \times 4 \times 3!}{3!} = 5 \times 4 = 20 \end{array}

\begin{array}{l} b) \\ ^{7} P_{3} = \frac{7!}{(7 - 3)!} = \frac{7!}{4!} \\ = \frac{7 \times 6 \times 5 \times 4!}{4!} = 7 \times 6 \times 5 = 210 \end{array}

\begin{array}{l} (c) \\ ^{9} P_{4} = \frac{9!}{(9 - 4)!} = \frac{9!}{5!} \\ = \frac{9 \times 8 \times 7 \times 6 \times 5!}{5!} = 9 \times 8 \times 7 \times 6 = 3024 \end{array}

Gunakan Kalkulator:

Bab 17 Pilir Atur dan Gabungan

Posted on October 3, 2016 by user

Bab 6 Pilir Atur dan Gabungan

6.1.1 Pilir Atur (Bahagian 1)

(A) Prinsip Pendaraban

Jika suatu peristiwa A boleh berlaku dalam r cara dan suatu peristiwa B boleh berlaku dalam s cara, maka bilangan cara peristiwa A boleh berlaku diikuti dengan berlakunya peristiwa B ialah r × s cara yang berlainan.

Contoh 1:

Terdapat 3 jalan raya berlainan dari bandar P ke bandar Q dan 4 jalan raya berlainan dari bandar Q ke bandar R. Cari bilangan cara seorang pemandu teksi boleh memilih untuk mengangkut pelancong dari bandar P ke bandar R melalui bandar Q.

Penyelesaian:

3 × 4 = 12

(B) Pilih Atur

Contoh 2:

Hitungkan setiap yang berikut:

(a) 7!
(b) 4!6!
(c) 0!5!

\begin{array}{l} (d) \frac{7!}{5!} \\ (e) \frac{8!}{4!} \\ (f) \frac{n!}{(n - 2)!} \\ (g) \frac{n! 0!}{(n - 1)!} \\ (h) \frac{3! (n + 1)!}{2! n!} \end{array}

Penyelesaian:

(a) 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

(b) 4!6! = (4 × 3 × 2 × 1)( 6 × 5 × 4 × 3 × 2 × 1) = 17280

(c) 0!5! = (1)( 5 × 4 × 3 × 2 × 1) = 120

\begin{array}{l} (d) \frac{7!}{5!} = \frac{7 \times 6 \times 5!}{5!} = 7 \times 6 = 42 \\ (e) \frac{8!}{4!} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{4!} = 8 \times 7 \times 6 \times 5 = 1680 \\ (f) \frac{n!}{(n - 2)!} = \frac{n (n - 1) (n - 2)}{(n - 2)} = n (n - 1) \\ (g) \frac{n! 0!}{(n - 1)!} = \frac{n (n - 1) (1)}{(n - 1)} = n \\ (h) \frac{3! (n + 1)!}{2! n!} = \frac{3 \times 2! (n + 1) (n) (n - 1)}{2! n (n - 1)} = 3 (n + 1) \end{array}

Gunakan Kalkulator: