8.1 Taburan Binomial
8.1.1 Kebarangkalian Sesuatu Peristiwa dalam Taburan Binomial
Dalam suatu taburan Binomial, kebarangkalian bahawa r kejayaan diperoleh dalam n percubaan tak bersandar diberi oleh
P (X = r) = nCr . pr. qn-r |
dengan
P = kebarangkalian
X = pembolehubah rawak diskret
r = bilangan kejayaan (0, 1, 2, 3, …, n)
n = bilangan percubaan
p = kebarangkalian memperoleh kejayaan (0 < p < 1)
q = kebarangkalian memperoleh kegagalan (q = 1 – p)
Contoh 1:
Kelvin melepaskan 3 tembakan dalam suatu sesi latihan menembak. Kebarangkalian bahawa Kelvin mengena sasaran ialah 0.6. X mewakili bilangan kali Kelvin mengena sasaran.
(a) Senaraikan unsur-unsur pemboleh ubah rawak diskret X yang bertaburan Binomial.
(b) Hitung kebarangkalian bagi setiap kejadian unsur X.
(c) Seterusnya, plot satu graf untuk mewakili kebarangkalian taburan binomial untuk X.
Penyelesaian:
(a)
X = Bilangan kali Kelvin mengena sasaran
X = {0, 1, 2, 3}
(b)
X ~ B (n, p)
X ~ B (3, 0.6)
P (X = r) = nCr . pr. qn-r
(i) P (X = 0)
= 3C0 (0.6)0 (0.4)3 ← (Kebarangkalian memperoleh kegagalan = 1 – 0.6 = 0.4)
= 0.064
(ii) P (X = 1)
= 3C1 (0.6)1 (0.4)2
= 0.288
(iii) P (X = 2)
= 3C2 (0.6)2 (0.4)1
= 0.432
(iv) P (X = 3)
= 3C3 (0.6)3 (0.4)0
= 0.216
(c)
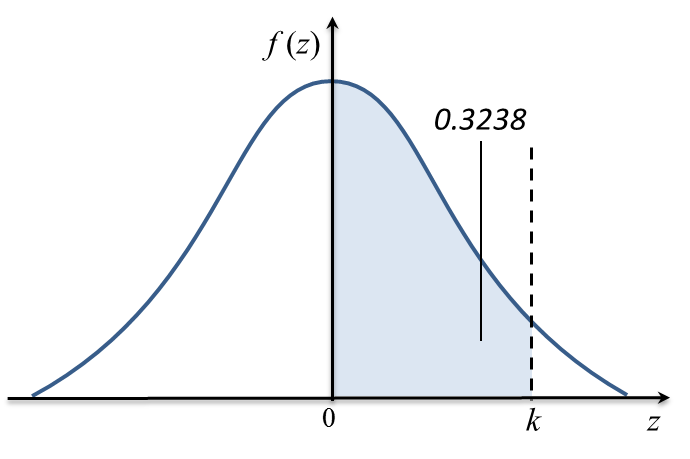
 P (Z > a) adalah luas rantau berlorek dalam rajah di atas.
P (Z > a) adalah luas rantau berlorek dalam rajah di atas.
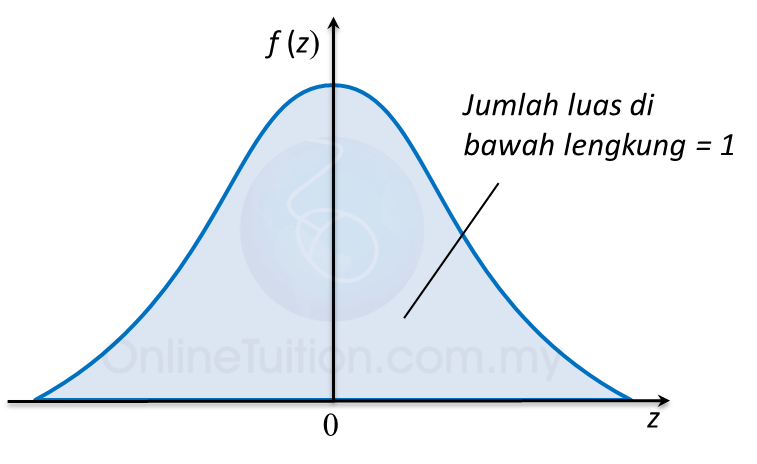
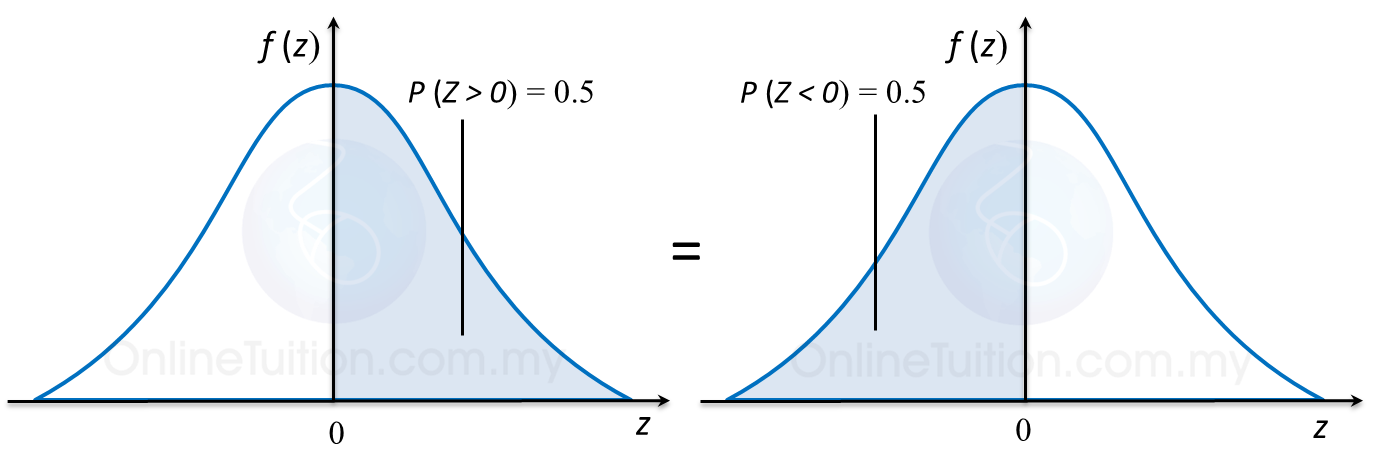
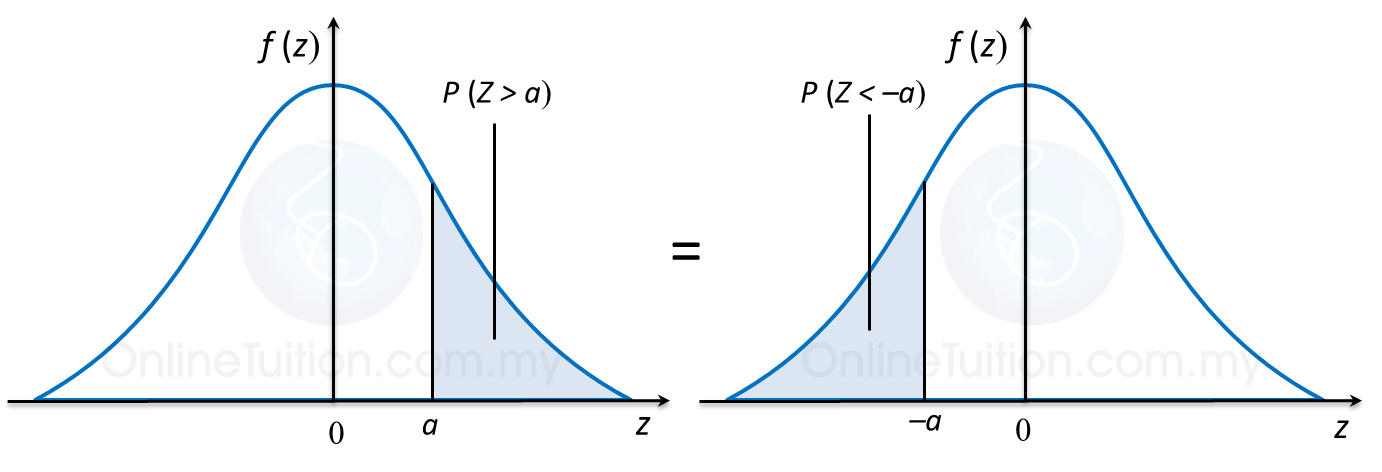
 P (Z > a) adalah luas rantau berlorek dalam rajah di atas.
P (Z > a) adalah luas rantau berlorek dalam rajah di atas.