1.1 Janjang Aritmetik
(A) Ciri-ciri Janjang Aritmetik
1. Jujukan ialah suatu set nombor yang mengikut suatu pola tertentu.Misalnya: 4, 7, 10, 13, … ialah satu jujukan.
2. Setiap nombor dalam suatu jujukan dikenali sebagai sebutan.
3. Janjang aritmetik (J.A.) ialah satu jujukan nombor yang setiap sebutan (kecuali sebutan pertama) diperoleh dengan menambahkan satu pemalar kepada sebutan sebelumnya. Pemalar ini dikenal sebagai beza sepunya, d.
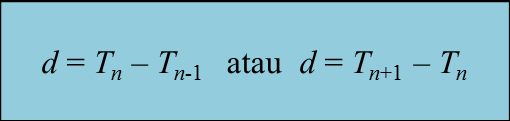
Contoh:
Tentukan sama ada jujukan nombor yang berikut ialan janjang aritmetik (J.A.) atau bukan janjang aritmetik.
(a) –5, –3, –1, 1, …
(b) 10, 7, 4, 1, -2, …
(c) 2, 8, 15, 23, …
(d) 3, 6, 12, 24, …
Tip pintar: Bagi suatu janjang aritmetik, anda sentiasa tambah atau tolak satu nombor tetap.
Penyelesaian:

(B) Langkah-langkah untuk membuktikan sama ada jujukan nombor yang diberi ialah satu janjang aritmetik
Langkah 1: Senaraikan tiga sebutan yang berturutan. [Contoh: T1 , T2 , T3 .]
Langkah 2: Hitung nilai bagi T3 − T2 dan T2 − T1 .
Langkah 3: Jika T3 − T2 = T2 − T1 = d, maka jujukan nombor itu ialah satu janjang aritmetik.
Contoh:
Buktikan sama ada jujukan nombor yang berikut ialah satu janjang aritmetik (J.A.).
(a) 7, 10, 13, …
(b) –20, –15, –9, …
Penyelesaian:
(a)
7, 10, 13 ← (Langkah 1: Senaraikan T1 , T2 , T3 )
T3 – T2 = 13 – 10 = 3 ← (Langkah 2: Cari T3 – T2 dan T2 – T1)
T2 – T1 = 10 – 7 = 3 ← (Langkah 2: Cari T3 – T2 dan T2 – T1)
T3 – T2 = T2 – T1
Maka, 7, 10, 13, … ialah J.A.
(b)
–20, –15, –9
T3 – T2 = –9 – (–15) = 6
T2 – T1 = –15 – (–20) = 5
T3 – T2 ≠ T2 – T1
Maka. –20, –15, –9, … bukan satu J.A.