Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

8.2 Panjang Lengkok Sesuatu Bulatan

(A) Rumus Panjang Lengkok dan Luas Bulatan

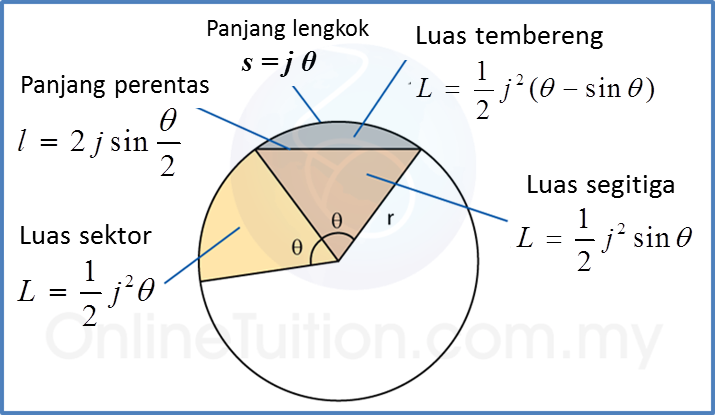
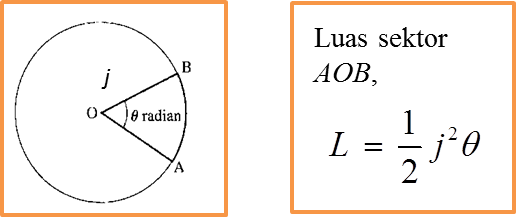
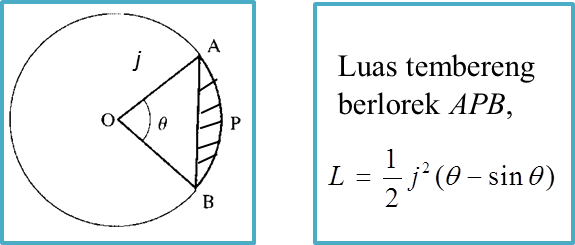
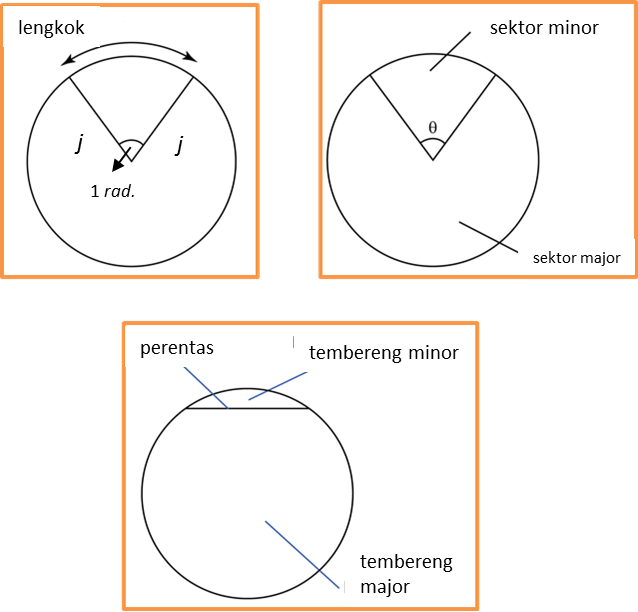
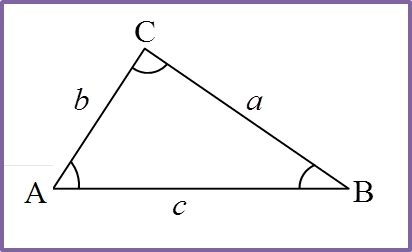
j = jejari, L= luas, s = panjang lengkok, θ = sudut dalam radian, l = panjang perentas

(B) Panjang Lengkok Sesuatu Bulatan

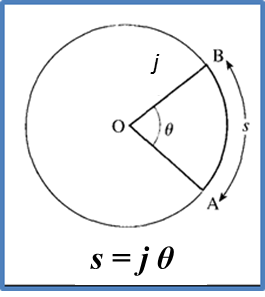
Contoh 1:

Suatu lengkok AB, yang berjejari 5 cm mencangkuk sudut 1.5 radian pada pusat bulatan.
Cari panjang lengkok AB.

Penyelesaian:

s = jθ

Panjang lengkok AB = (5)(1.5) = 7.5 cm

Contoh 2:

Suatu lengkok PQ, yang berjejari 12 cm mencangkuk sudut 30^opada pusat bulatan.
Cari panjang lengkok PQ.

Penyelesaian:

Panjang lengkok PQ

\begin{array}{l} = 12 \times 30^{\circ} \times \frac{π}{180^{\circ}} \\ = 6.283 cm \end{array}

Contoh 3:

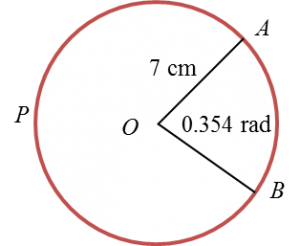
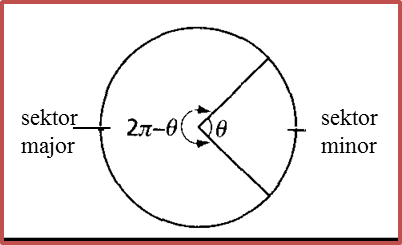
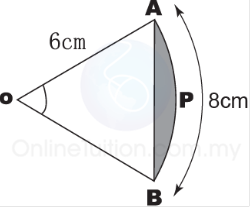
Bagi rajah di atas, cari

(a) panjang lengkok minor AB

(b) panjang lengkok major APB

Penyelesaian:

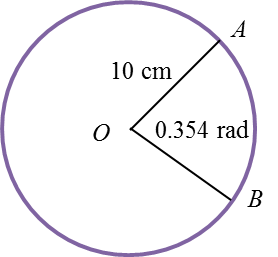
(a)

panjang lengkok minor AB = jθ

= (7)(0.354)

= 2.478 cm

(b)

360^o = 2π radian, sudut refleks AOB

= (2π – 0.354) radian.

Panjang lengkok major APB

= 7 × (2π – 0.354)

= 7 × [(2)(3.1416) – 0.354]

= 7 × 5.9292

= 41.5044 cm

Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

8.3 Luas Sektor Sesuatu Bulatan

(A) Luas Sektor Sesuatu Bulatan

1. Jika sesuatu bulatan dibahagikan kepada dua sektor yang berlainan saiz, sektor yang lebih kecil dikenali sebagai sektor minor manakala sektor yang lebih besar dikenali sebagai sektor major.

2. Jika AOB ialah luas sektor suatu bulatan yang berjejari j, dan sudut θ radian yang tercangkum pada pusat bulatan O, maka

Contoh 1:

Dalam rajah di atas, cari luas sektor OAB.

Penyelesaian:

Luas sektor OAB

= ½ j²θ

= ½ (10)²(0.354)

= 17.7 cm²

(B) Mencari Luas Tembereng Sesuatu Bulatan

Contoh 2:

Rajah di atas menunjukkan sebuah sector bulatan yang berpusat O yang mempunyai jejari 6 cm.
Panjang lengkok AB ialah 8 cm. Cari

(i) ∠ AOB

(ii) luas tembereng berlorek.

Penyelesaian:

(i) Panjang lengkok AB = 8 cm

jθ = 8

6θ = 8

θ = 1.333 radian

∠AOB = 1.333 radian

(ii)

Luas tembereng berlorek

= ½ j² (θ – sinθ) (pastikan kalkulator dalam Mod Radian)

= ½ (6)² (1.333 – sin1.333)

= ½ (36) (1.333 – 0.972)

= 6.498 cm²

Bab 8 Sukatan Membulat

Posted on May 27, 2016 by user

Bab 8 Sukatan Membulat

8.1 Radian

(A) Takrifan Radian

(B) Menukar Ukuran dalam Darjah kepada Radian:

(C) Menukar Ukuran dalam Radian kepada Darjah:

Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

10.4.2 Penyelesaian Segitiga, SPM Praktis (Kertas 2)

Soalan 2:

Rajah menunjukkan trapezium PQRS. PS adalah selari dengan QR dan ∠QRS ialah sudut cakah. Cari
(a) panjang, dalam cm, QS.
(b) panjang, dalam cm, RS.
(c) ∠QRS.
(d) luas, dalam cm², segitiga QRS.

Penyelesaian:

(a)

\begin{array}{l} \frac{Q S}{\sin P} = \frac{P S}{\sin Q} \\ \frac{Q S}{\sin 85^{\circ}} = \frac{13.1}{\sin 28^{\circ}} \\ Q S = \frac{13.1 \times \sin 85^{\circ}}{\sin 28^{\circ}} \\ Q S = 27.8 cm \end{array}

(b)

∠RQS = 180^o– 85^o – 28^o

∠RQS = 67^o

Guna petua kosinus,

RS² = QR²+ QS² – 2 (QR)(QS) kos ∠RQS

RS² = 6.4² + 27.8² – 2 (6.4)(27.8) kos 67^o

RS² = 813.8 – 139.04

RS² = 674.76

RS = 25.98 cm

(c)

Guna petua kosinus,

QS² = QR²+ RS² – 2 (QR)(RS) kos ∠RQS

27.8² = 6.4²+ 25.98² – 2 (6.4)(25.98) kos∠QRS

772.84 = 715.92 – 332.54 kos∠QRS

kos ∠ Q R S = \frac{715.92 - 772.84}{332.54}

kos∠QRS = –0.1712

∠QRS = 99.86^o

(d)

Luas segitiga QRS

= ½ (QR)(RS) sin R

= ½ (6.4) (25.98) sin 99.86^o

= 81.91 cm²

Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

Bab 10 Penyelesaian Segitiga

10.1 Petua Sinus

Dalam suatu segitiga ABC, huruf besar A, B, C digunakan untuk mewakili sudut di bucu-bucu A, B dan C masing-masing. Huruf kecil a, b, dan c untuk mewakili sisi BC, CA dan AB yang bertentangan dengan bucunya.

Petua sinus boleh digunakan untuk menyelesaikan sesuatu segitiga apabila
(i) dua sudut dan satu sisi diberikan, atau
(ii) dua sisi dan satu sudut bukan kandung diberikan

(A) Jika 2 sudut dan 1 sisi diketahui ⇒ Petua Sinus

Contoh:

Hitung panjang AB, dalam cm.

Penyelesaian:

∠ACB = 180^o – (50^o + 70^o) = 60^o

\begin{array}{l} \frac{A B}{\sin 60^{o}} = \frac{4}{\sin 50^{o}} \\ A B = \frac{4 \times \sin 60^{o}}{\sin 50^{o}} \\ A B = 4.522 cm \end{array}

(B) Jika 2 sisi dan 1 sudut diketahui (bukan di antara sisi) ⇒ Petua Sinus

Contoh:

Hitung ∠ACB

Penyelesaian:

\begin{array}{l} \frac{28}{\sin 54^{o}} = \frac{26}{\sin ∠ A C B} \\ \sin ∠ A C B = \frac{26 \times \sin 54^{o}}{28} \\ \sin ∠ A C B = 0.7512 \\ ∠ A C B = {48.7}^{o} \end{array}

(C) Mencari Sisi atau Sudut dalam Sesuatu Segitiga bagi Kes Berambiguiti

Contoh:

Hitung ∠ACB, θ.

Penyelesaian:

Dalam kes ini, terdapat dua kemungkinan dalam bentuk sigitiga.

AB = 26cm BC = 28 cm ∠ BAC = 54^o

\frac{26}{\sin θ} = \frac{28}{\sin 54^{o}}

sin θ = 0.7512

θ = sin ^-10.7512

θ = 48.7^o, 180^o – 48.7^o

θ = 48.7^o(sudut tirus), 131.3^o (sudut cakah)

Bab 10 Penyelesaian Segitiga

Posted on May 27, 2016 by user

10.2 Petua Kosinus

a² = b²+ c² – 2bc kosA

b² = a²+ c² – 2ac kosB

c² = a²+ b² – 2ab kosC

Petua kosinus boleh digunakan untuk menyelesaikan sesuatu segitiga apabila
(i) dua sisi dan satu sudut kandung diberikan, atau
(ii) tiga sisi diberikan

(A) Jika 2 sisi dan 1 sudut kandung diberi ⇒ Petua Kosinus

Contoh:

Hitung panjang AC, x, dalam cm bagi segitiga di atas.

Penyelesaian:

b² = a²+ c² – 2ac kosB

x² = 4² + 7² – 2(4)(7) kos50^o

x² = 16 + 49 – 56 (0.6428)

x² = 65 – 35.997

x² = 29.003

x = 5.385 cm

(B) Jika 3 sisi diberi ⇒ Petua Kosinus

Contoh:

Hitung ∠BAC

Penyelesaian:

\begin{array}{l} k o s A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} \\ k o s ∠ B A C = \frac{7^{2} + 6^{2} - 8^{2}}{2 (7) (6)} \end{array}

kos∠BAC = 0.25

∠BAC = kos ^-10.25

∠BAC = 75.52^o

Bab 10 Penyelesaian Segitiga

Posted on May 26, 2016 by user

10.4.1 Penyelesaian Segitiga, SPM Praktis (Kertas 2)

Soalan 1:

Rajah di bawah menunjukkan sisi empat ABCD.

Luas segitiga BCD ialah 12 cm² dan ∠BCD ialah tirus. Hitung
(a) ∠BCD,
(b) Panjang, dalam cm, bagi BD,
(c) ∠ABD,
(d) luas, dalam cm², sisi empat ABCD.

Penyelesaian:

(a)

Diberi luas ∆ BCD = 12 cm²

½ (BC) (CD) sin C = 12

½ (7) (4) sin C= 12

14 sin C = 12

sin C = 12/14 = 0.8571

C = 59^o

∠BCD = 59^o

(b)

Guna petua kosinus,

BD² = CD² + BC² – 2 (4)(7) kos 59^o

BD² = 4² + 7² – 2 (4)(7) kos 59^o

BD² = 65 – 28.84

BD² = 36.16

BD = 6.013 cm

(c)

Guna petua sinus,

\begin{array}{l} \frac{A B}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \frac{10}{\sin 35^{\circ}} = \frac{6.013}{\sin A} \\ \sin A = \frac{6.013 \times \sin 35^{\circ}}{10} \end{array}

sin A = 0.3449

A = 20.18^o

∠ABD = 180^o– 35^o – 20.18^o

= 124.82^o

(d)

Luas sisi empat ABCD

= Luas ∆ ABD + Luas ∆ BCD

= ½ (AB)(BD) sin B + 12 cm

= ½ (10) (6.013) sin 124.82 + 12

= 24.68 + 12

= 36.68 cm

Bab 10 Penyelesaian Segitiga

Posted on May 26, 2016 by user

10.3 Luas Segitiga

Luas segitiga = ½ absinC

Contoh:

Hitung luas segitiga rajah di atas.

Penyelesaian:

Luas ∆ = ½ ab sinC

= ½ (7)(4) sin40^o

= 9 cm²

Contoh:

Rajah di atas menunjukkan sebuah segi tiga ABC, dengan keadaan AC = 8 cm dan ∠ C = 32^o . Titik D terletak pada garis BC dengan keadaan BD = 10 cm dan ∠ ADB = 70^o . Hitungkan
(a) panjang CD,
(b) luas ∆ ADC,
(c) luas ∆ ABC,
(d) panjang AB.

Penyelesaian:
(a)

\begin{array}{l} ∠ A D C + 70^{o} = 180^{o} \\ ∠ A D C = 110^{o} \\ ∠ C A D = 180^{o} - 110^{o} - 32^{o} \\ ∠ C A D = 38^{o} \\ Guna Petua Sinus, \\ \frac{8}{\sin 110^{o}} = \frac{C D}{\sin 38^{o}} \\ C D \sin 110^{o} = 8 \sin 38^{o} \\ C D (0.940) = 8 (0.616) \\ C D = 5.243 \end{array}

(b)

\begin{array}{l} Luas △ A D C \\ = \frac{1}{2} (8) (5.243) sin 32^{o} \\ = 20.972 (0.530) \\ = 11.12 {cm}^{2} \end{array}

(c)

\begin{array}{l} Luas △ A B C \\ = \frac{1}{2} (8) (10 + 5.243) sin 32^{o} \\ = 60.972 (0.530) \\ = 32.315 {cm}^{2} \end{array}

(d)

\begin{array}{l} Guna Petua kosinus bagi △ A B C, \\ A B^{2} = {15.243}^{2} + 8^{2} - 2 (15.243) (8) k o s 32^{o} \\ A B^{2} = 232.35 + 64 - 206.83 \\ A B^{2} = 89.52 \\ A B = 9.462 cm \end{array}

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 2:

Rajah menunjukkan trapezium PQRS. Diberi persamaan PQialah 2y – x – 5 = 0, cari

(a) nilai w,

(b) persamaan PS dan seterusnya cari koordinat P,

(c) lokus M supaya segitiga QMS adalah sentiasa berserenjang di M.

Penyelesaian:

(a)

Persamaan PQ,

2y – x – 5 = 0

2y = x + 5

\begin{array}{l} y = \frac{1}{2} x + \frac{5}{2} \\ ∴ m_{P Q} = \frac{1}{2} \\ In a trapizium, m_{P Q} = m_{S R} \\ \frac{1}{2} = \frac{0 - (- 3)}{w - 4} \\ w - 4 = 6 \\ w = 10 \end{array}

(b)

\begin{array}{l} m_{P Q} = \frac{1}{2} \\ m_{P S} = - \frac{1}{m_{P Q}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Titik S = (4, –3), m = –2

y – y₁ = m (x– x₁)

y – (–3) = –2 (x – 4)

y + 3 = –2x + 8

y = –2x + 5

Persamaan PS ialah y = –2x + 5

PS is y = –2x + 5-----(1)

PQ is 2y = x + 5-----(2)

Gantikan (1) ke dalam (2)

2 (–2x + 5) = x + 5

–4x + 10 = x + 5

–5x = –5

x = 1

Dari (1), y = –2(1) + 5

y = 3

Koordinat titik P = (1, 3).

(c)

Katakan M = (x, y)

Diberi ∆QMS berserenjang di M

Oleh itu, ∆QMS = 90^o

(m_QM) (m_MS) = –1

(\frac{y - 5}{x - 5}) (\frac{y - (- 3)}{x - 4}) = - 1

(y – 5) (y + 3) = –1(x– 5) (x – 4)

y² + 3y – 5y – 15 = –1(x² – 4x – 5x + 20)

y² – 2y – 15 = –x² + 9x – 20

x² + y²– 9x – 2y + 5 = 0

Jadi, persamaan lokus titik M ialah

x² + y² – 9x – 2y + 5 = 0.

Bab 6 Geometri Koordinat

Posted on May 26, 2016 by user

6.8 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 1:

Rajah menunjukkan garis lurus PQ bertemu dengan garis lurus RSdi titik Q. Titik P terletak pada paksi-y.

(a) Tuliskan persamaan RS dalam bentuk pintasan.

(b) Diberi 2RQ = QS, cari koordinat Q.

(c) Diberi PQ berserenjang dengan RS, cari pintasan-y bagi PQ.

Penyelesaian:

(a)

\begin{array}{l} \frac{x}{12} + \frac{y}{- 6} = 1 \\ \frac{x}{12} - \frac{y}{6} = 1 \end{array}

(b)

Diberi 2RQ = QS

\begin{array}{l} \frac{R Q}{Q S} = \frac{1}{2} \\ Katakan koordinat Q = (x, y) \\ (\frac{(0) (2) + (12) (1)}{1 + 2}, \frac{(- 6) (2) + (0) (1)}{1 + 2}) = (x, y) \\ x = \frac{12}{3} = 4 \\ y = - \frac{12}{3} = - 4 \\ Q = (4, - 4) \end{array}

(c)

\begin{array}{l} Kecerunan R S, m_{R S} \\ = - (\frac{- 6}{12}) = \frac{1}{2} \\ m_{P Q} = - \frac{1}{m_{R S}} = - \frac{1}{\frac{1}{2}} = - 2 \end{array}

Titik Q = (4, –4), m = –2

Guna y = mx+ c

–4 = –2 (4) + c

c = 4

Maka, pintasan-y bagi PQ = 4