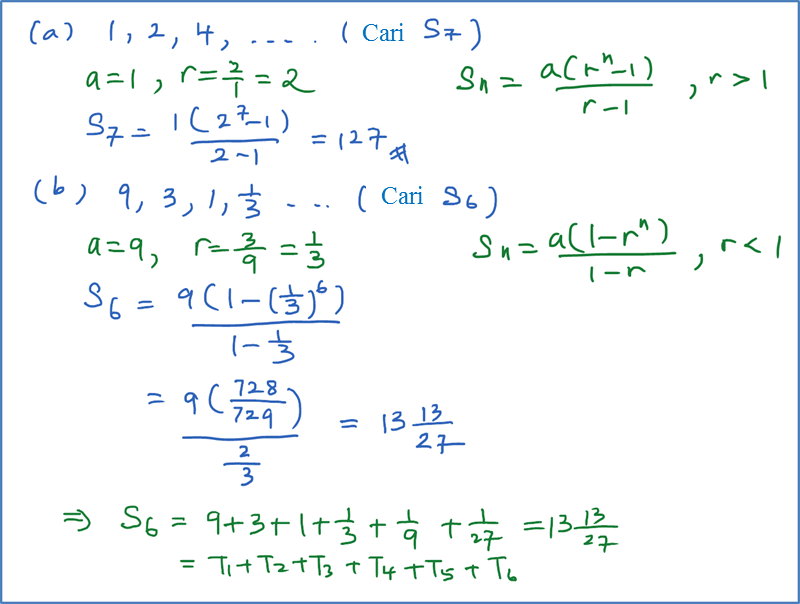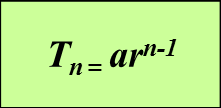Bab 12 Janjang

Posted on May 21, 2016 by user

1.2.5 Hasil Tambah Janjang Geometri Sehingga Ketakterhinggaan

(G) Mencari Hasil Tambah Janjang Geometri Sehingga Ketakterhinggaan

S \infty = \frac{a}{1 - r}, - 1 < r < 1

a = sebutan pertama

r = nisbah sepunya

S∞ = hasil tambah sehingga ketakterhinggaan

Contoh:

Cari hasil tambah setiap siri yang berikut sehingga ketakterhinggaan.

(a) 8, 4, 2, ...

(b)

\frac{2}{3}, \frac{2}{9}, \frac{2}{27}, .....

(c) 3, 1, ⅓, ….

Penyelesaian:

(a)

8, 4, 2, ….

a = 2, r = 4/8 = ½

S∞ = 8 + 4 + 2 + 0.5 + 0.25 + 0.125 + 0.0625 + 0.03125 + …..

S \infty = \frac{a}{1 - r} = \frac{2}{1 - \frac{1}{2}} = 4

(b)

\begin{array}{l} \frac{2}{3}, \frac{2}{9}, \frac{2}{27}, ..... \\ a = \frac{2}{3}, r = \frac{2 / 9}{2 / 3} = \frac{1}{3} \\ S \infty = \frac{a}{1 - r} \\ S \infty = \frac{\frac{2}{3}}{1 - \frac{1}{3}} = 1 \end{array}

(c)

\begin{array}{l} 3, 1, \frac{1}{3}, ..... \\ a = 3, r = \frac{1}{3} \\ S \infty = \frac{a}{1 - r} \\ S \infty = \frac{3}{1 - \frac{1}{3}} = \frac{3}{2 / 3} = \frac{9}{2} \end{array}

(H) Perpuluhan Jadi Semula

Contoh bagi perpuluhan jadi semula:

\begin{array}{l} \frac{2}{9} = 0.2222222222222..... \\ \frac{8}{33} = 0.242424242424..... \\ \frac{41}{333} = 0.123123123123..... \end{array}

Perpuluhan jadi semula boleh ditukar kepada pecahan dengan menggunakan rumus hasil tambah sehingga ketakterhinggaan

S \infty = \frac{a}{1 - r}

Contoh (Tukar perpuluhan jadi semula kepada pecahan)

Ungkapkan setiap perpuluhan jadi semula yang berikut sebagai suatu pecahan dalam bentuk yang paling ringkas.

(a) 0.8888 ...

(b) 0.171717...

(c) 0.513513513 ….

Penyelesaian:

(a)

0.8888 = 0.8 + 0.08 + 0.008 +0.0008 + ….. (perpuluhan jadi semula )

\begin{array}{l} J G, a = 0.8, r = \frac{0.08}{0.8} = 0.1 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.8}{1 - 0.1} \\ S_{\infty} = \frac{0.8}{0.9} \\ S_{\infty} = \frac{8}{9} \to \begin{array}{l} Semakan kalkulator \\ \frac{8}{9} = 0.888888.... \end{array} \end{array}

(b)

0.17171717 …..

= 0.17 + 0.0017 + 0.000017 + 0.00000017 + …..

\begin{array}{l} J G, a = 0.17, r = \frac{0.0017}{0.17} = 0.01 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.17}{1 - 0.01} = \frac{0.17}{0.99} = \frac{17}{99} \to \begin{array}{l} Peringatan: \\ semak jawapan \\ dengan kalkulator \end{array} \end{array}

(c)

0.513513513…..

= 0.513 + 0.000513 + 0.000000513 + …..

\begin{array}{l} J G, a = 0.513, r = \frac{0.00513}{0.513} = 0.001 \\ S_{\infty} = \frac{a}{1 - r} \\ S_{\infty} = \frac{0.513}{1 - 0.001} = \frac{0.513}{0.999} = \frac{513}{999} = \frac{19}{37} \end{array}

Bab 12 Janjang

Posted on May 21, 2016 by user

1.2.3 Hasil Tambah Suatu Janjang Geometri

(F) Hasil Tambah n sebutan pertama suatu Janjang Geometri

\begin{array}{l} S_{n} = \frac{a (r^{n} - 1)}{r - 1}, r > 1 \\ S_{n} = \frac{a (1 - r^{n})}{1 - r}, r < 1 \end{array}

a = sebutan pertama

r = nisbah sepunya

n = bilangan sebutan

S_n = hasil tambah n sebutan pertama

Contoh 1:

Cari hasil tambah bagi setiap janjang geometri yang berikut.

(a) 1, 2, 4, ... sehingga 7 sebutan pertama

(b) 9, 3, 1, ⅓, ... sehingga 6 sebutan pertama

(c) 12, 3, ....,

\frac{3}{64}

[Tip pintar: bilangan sebutan,n dalam suatu janjang aritmetik dapat dicari jika sebutan terakhir diketahui]

Penyelesaian:

Bab 12 Janjang

Posted on May 21, 2016 by user

1.2.3 Menetukan Sebutan Tertentu dan Bilangan Sebutan dalam Suatu Janjang Geometri (Contoh Soalan)

Contoh 1:

Sebutan ke-6 dan sebutan ke-3 dalam suatu janjang geometri masing-masing ialah 32 dan 4. Hitung sebutan pertama dan nisbah sepunya.

Penyelesaian:

T₆ = 32

ar⁵ = 32 ----- (1)

T₃ = 4

ar² = 4 ----- (2)

\frac{(1)}{(2)} = \frac{a r^{5}}{a r^{2}} = \frac{32}{4}

r³ = 8

r = 2

Gantikan r = 2 ke dalam (2),

a (2)²= 4

a = 1

Contoh 2:

Dalam suatu janjang geometri, hasil tambah sebutan ke-2 dan sebutan ke-3 ialah 12 dan hasil tambah sebutan ke-3 dan sebutan ke-4 ialah 4, cari sebutan pertama dan nisbah sepunya.

Penyelesaian:

T₂+ T₃= 12

ar + ar²= 12

ar (1 + r) = 12 ----- (1) ← (Pemfaktoran)

T₃+ T₄= 4

ar² + ar³= 4

ar² (1 + r) = 4 ----- (2)

Contoh 3:

Untuk janjang geometri 3, 12, 48, , ... Cari nilai terkecil n supaya sebutan ke-n melebihi 1 000 000.

Penyelesaian:

\begin{array}{l} 3, 12, 48, ..... \\ J G, a = 3, r = \frac{T_{2}}{T_{1}} = \frac{12}{3} = 4 \\ T_{n} > 1000000 \\ (3) {(4)}^{n - 1} > 1000000 \\ {(4)}^{n - 1} > \frac{1000000}{3} \leftarrow [(3) {(4)}^{n - 1} \neq 12^{n - 1}] \\ \log 4^{n - 1} > \log \frac{1000000}{3} \leftarrow (L e t a k log di \\ kedua-dua belah) \\ (n - 1) \lg 4 > \lg \frac{1000000}{3} \leftarrow (\log_{a} m^{n} = n \log_{a} m) \end{array}

(n – 1)(0.6021) > 5.523

n – 1 > 9.17

n > 10.17

n = 11 ← (n ialah integer)

Semakan:

T₁₁= (3)(4)¹⁰

T₁₁= 3 145 728 > 1 000 000

Bab 12 Janjang

Posted on May 21, 2016 by user

1.2.2 Menetukan Sebutan Tertentu dan Bilangan Sebutan dalam Suatu Janjang Geometri

(C) Sebutan Tertentu dalam Suatu Janjang Geometri

a = sebutan pertama
r = nisbah sepunya

n = bilangan sebutan

T_n = sebutan ke-n

Contoh:

Cari sebutan yang diberi bagi setiap janjang geometri yang berikut.

(a) 8 ,4 ,2 ,...... T₈

(b)

\frac{16}{27}, \frac{8}{9}, \frac{4}{3}, .....

, T₆

Penyelesian:

T_n = arⁿ^-1

T₁ = ar^1-1 = ar⁰ = a ← (sebutan pertama)

T₂ = ar^2-1 = ar¹ = ar ← (sebutan kedua)

T₃ = ar^3-1 = ar² ← (sebutan ketiga)

T₄ = ar^4-1 = ar³ ← (sebutan keempat)

(a)

\begin{array}{l} 8, 4, 2, ..... \\ a = 8, r = \frac{4}{8} = \frac{1}{2} \\ T_{8} = a r^{7} \\ T_{8} = 8 {(\frac{1}{2})}^{7} = \frac{1}{16} \end{array}

(b)

\begin{array}{l} \frac{16}{27}, \frac{8}{9}, \frac{4}{3}, ..... \\ a = \frac{16}{27} \\ r = \frac{T_{2}}{T_{1}} = \frac{\frac{16}{27}}{\frac{8}{9}} = \frac{2}{3} \\ T_{6} = a r^{5} \\ = \frac{16}{27} {(\frac{2}{3})}^{5} = \frac{512}{6561} \end{array}

(D) Bilangan Sebutan dalam Suatu Janjang Geometri

Tip pintar: Bilangan sebutan dalam suatu janjang geometri dapat dicari jika sebutan terakhir
diketahui.

Contoh:

Cari bilangan sebutan bagi setiap janjang geometri yang berikut.

(a) 2, 4, 8, ….., 8192

(b)

\frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729}

(c) –½, 1, –2, ….., 64

Penyelesian:

(a)

2, 4, 8, ….., 8192 ← (sebutan terakhir diberi)

a = 2

r = \frac{T_{2}}{T_{1}} = \frac{4}{2} = 2

T_n= 8192

arⁿ^-1= 8192 ← T_n = arⁿ^-1

(2)(2)ⁿ^-1 = 8192

2ⁿ^-1 = 4096

2ⁿ^-1 = 2¹²

n– 1 = 12

n = 13

(b)

\begin{array}{l} \frac{1}{4}, \frac{1}{6}, \frac{1}{9}, ....., \frac{16}{729} \\ a = \frac{1}{4}, r = \frac{\frac{1}{6}}{\frac{1}{4}} = \frac{2}{3} \\ T_{n} = \frac{16}{729} \\ a r^{n - 1} = \frac{16}{729} \\ (\frac{1}{4}) {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \\ {(\frac{2}{3})}^{n - 1} = \frac{16}{729} \times 4 \\ {(\frac{2}{3})}^{n - 1} = \frac{64}{729} \\ {(\frac{2}{3})}^{n - 1} = {(\frac{2}{3})}^{6} \\ ∴ n - 1 = 6 \\ n = 7 \end{array}

(c)

\begin{array}{l} - \frac{1}{2}, 1, - 2, ....., 64 \\ a = - \frac{1}{2}, r = \frac{- 2}{1} = - 2 \\ T_{n} = 64 \\ a r^{n - 1} = 64 \\ (- \frac{1}{2}) {(- 2)}^{n - 1} = 64 \end{array}

T_n= 64

arⁿ^-1= 64

(–½)(–2)ⁿ^-1 = 64

(–2)ⁿ^-1 = 64 × –2

(–2)ⁿ^-1 = –128

(–2)ⁿ^-1 = (–2)⁷

n– 1 = 7

n = 8

(E) Tiga sebutan Berturutan dalam suatu janjang geometri (J.G.)

Jika e, f dan g adalah 3 sebutan berturutan dalam suatu janjang geometri (JG), maka

\frac{g}{f} = \frac{f}{e}

Contoh:

Jika p + 20, p − 4, p −20 adalah 3 sebutan berturutan dalam suatu janjang geometri, cari niali p.

Penyelesian:

\frac{p - 20}{p - 4} = \frac{p - 4}{p + 20}

(p + 20)(p – 20) = (p – 4)(p – 4)

p²– 400 = p² – 8p + 16

8p = 416

p = 52

Bab 12 Janjang

Posted on May 21, 2016 by user

1.1.2a Menetukan Sebutan Tertentu dalam Suatu Janjang Aritmetik (Contoh Soalan)

Contoh 1:

Jika sebutan ke-20 dalam suatu janjang aritmetik ialah 14 dan sebutan ke-40 ialah – 6,

Cari

(a) sebutan pertama dan beza sepunya,

(b) sebutan ke-10.

Penyelesian:

(a)

T₂₀ = 14

a + 19d = 14 ----- (1) ← (T_n= a + (n– 1) d

T₄₀ = – 6

a + 39d = – 6 ----- (2)

(2) – (1),

20d = – 20

d = – 1

Gantikan d = – 1 ke dalam (1),

a + 19 (– 1) = 14

a = 33

(b)

T₁₀ = a + 9d

T₁₀ = 33 + 9 (– 1)

T₁₀ = 24

Contoh 2:

Sebutan ke-3 dan sebutan ke-7 dalam suatu janjang aritmetik ialah 20 dan 12 masing-masing.

(a) Hitung sebutan ke-20.

(b) Cari sebutan dengan nilainya ialah – 34.

Penyelesian:

(a)

T₃ = 20

a + 2d = 20 ----- (1) ← (T_n= a + (n – 1) d

T₇ = 12

a + 6d = 12 ----- (2)

(2) – (1),

4d = – 8

d = – 2

Gantikan d = – 2 ke dalam (1),

a + 2 (– 2) = 20

a = 24

T₂₀ = a + 19d

T₂₀ = 24 + 19 (– 2)

T₂₀ = –4

(b)

T_n = –34

a + (n – 1) d = –34

24 + (n – 1) (–2) = –34

(n – 1) (–2) = –58

n – 1 = 29

n = 30

Contoh 3:

Tiga sebutan pertama dalam suatu janjang aritmetik ialah 72, 65 dan 58.

Sebutan ke-n bagi janjang ini adalah negatif.

Cari nilai terkecil n.

Penyelesian:

72, 65, 58

JA, a = 72, d = 65 – 72 = –7

Sebutan ke-n adalah negatif,

T_n< 0

a + (n – 1) d < 0

72 + (n – 1) (–7) < 0

(n – 1) (–7) < –72

n – 1 > –72/ –7

n – 1 > 10.28

n > 11.28

n mestilah satu integer, n = 12, 13, 14, ….

Maka nilai terkecil n = 12.

Bab 12 Janjang

Posted on May 20, 2016 by user

(F) Hasil Tambah n Sebutan Pertama suatu Janjang Aritmetik

Hasil Tambah n Sebutan Pertama suatu Janjang Aritmetik

\begin{array}{l} S_{n} = \frac{n}{2} [2 a + (n - 1) d] \\ S_{n} = \frac{n}{2} (a + l) \end{array}

a = sebutan pertama

d = beza sepunya

n = bilangan sebutan

S_n = hasil tambah nsebutan pertama

Contoh:

Hitung hasil tambah bagi setiap janjang aritmetik yang berikut:

(a) –11, –8, –5, ... sehingga 15 sebutan pertama.

(b) 8, 10½, 13,... sehingga 15 sebutan pertama.

(c) 5, 7, 9,....., 75 [Tip pintar: bilangan sebutan,n dalam suatu janjang aritmetik dapat dicari jika sebutan terakhir diketahui]

Penyelesaian:

(a)

–11, –8, –5, ...Cari S₁₅

a = –11

d = –8 – (–11) = 3

\begin{array}{l} S_{15} = \frac{15}{2} [2 a + 14 d] \\ S_{15} = \frac{15}{2} [2 (- 11) + 14 (3)] = 150 \end{array}

(b)

8, 10½, 13,... Cari S₁₃

a = 8

\begin{array}{l} d = 10 \frac{1}{2} - 8 = \frac{5}{2} \\ S_{13} = \frac{13}{2} [2 a + 12 d] \\ S_{13} = \frac{13}{2} [2 (8) + 12 (\frac{5}{2})] = 299 \end{array}

(c)

5, 7, 9,..., 75 ← (sebutan terakhir l ialah 75)

a = 5

d = 7 – 5 = 2

sebutan terakhir l= 75

T_n = 75

a + (n – 1)d = 75

5 + (n – 1)(2) = 75

(n – 1)(2) = 70

n – 1 = 35

n = 36

\begin{array}{l} S_{n} = \frac{n}{2} (a + l) \\ S_{36} = \frac{36}{2} (5 + 75) = 1440 \end{array}

Bab 12 Janjang

Posted on May 20, 2016 by user

1.1.2 Menetukan Sebutan Tertentu dan Bilangan Sebutan dalam Suatu Janjang Aritmetik

(C) Menentukan Sebutan Tertentu dalam suatu Janjang Aritmetik (J.A.)

T_n= a + (n − 1) d

dengan keadaan

a = sebutan pertama

d = beza sepunya

n = bilangan sebutan

T_n = sebutan ke-n

(D) Bilangan Sebutan dalam suatu Janjang Aritmetik (J.A.)

Tip pintar: Bilangan sebutan dalam suatu janjang aritmetik dapat dicari jika sebutan terakhir diketahui.

Contoh 1:

Cari bilangan sebutan bagi setiap janjang aritmetik yang berikut.

(a) 5, 9, 13, 17... , 121

(b) 1, 1.25, 1.5, 1.75,..., 8

Penyelesaian:

(a)

5, 9, 13, 17... , 121

JA,

a = 5, d = 9 – 5 = 4

Sebutan terakhir, T_n = 121

a + (n – 1) d = 121

5 + (n – 1) (4) = 121

(n – 1) (4) = 116

(n – 1) =

\frac{116}{4}

= 29

n = 30

(b)

1, 1.25, 1.5, 1.75,..., 8

JA,

a = 1, d = 1.25 – 1 = 0.25

T_n = 8

a + (n – 1) d = 8

1 + (n – 1) (0.25) = 8

(n – 1) (0.25) = 7

(n – 1) = 28

n = 29

(E) Sebutan Berturutan dalam suatu Janjang Aritmetik (J.A.)

Jika a, b, c ialah tiga sebutan berturutan

dalam suatu janjang aritmetik, maka

c – b = b – a

Contoh 2:

Jika x + 1, 2x + 3 dan 6 ialah tiga sebutan yang berturutan dalam suatu janjang aritmetik, cari nilai x dan beza sepunya.

Penyelesaian:

x + 1, 2x + 3, 6

c – b = b– a

6 – (2x + 3) = (2x + 3) – (x + 1)

6 – 2x – 3 = 2x + 3 – x – 1

3 – 2x = x + 2

\begin{array}{l} x = \frac{1}{3} \\ \frac{1}{3} + 1, 2 (\frac{1}{3}) + 3, 6 \\ \frac{4}{3},  3 \frac{2}{3},  6 \\ d = 3 \frac{2}{3} - \frac{4}{3} = 2 \frac{1}{3} \end{array}

Bab 3 Fungsi Kuadratik

Posted on May 20, 2016 by user

3.2c Cari Titik Maksimum atau Titik Minimum suatu Fungsi Kuadratik dengan Kaedah Penyempurnaan Kuasa Dua (Contoh Soalan)

Contoh:

Dengan menggunakan kaedah penyempurnaan kuasa dua, nyatakan nilai maksimum atau nilai minimum bagi setiap fungsi kuadratik yang berikut.

Seterusnya, cari titik maksimum atau titik minimum dan nyatakan paksi simetri yang sepadan.

(a) f (x ) = x ² + 6x + 7

(b) f (x ) = 2x ² – 6x + 7

(d) f (x ) = 4 + 12x – 3x ²

Penyelesaian:

Bab 3 Fungsi Kuadratik

Posted on May 20, 2016 by user

3.2.2 Cari Titik Maksimum atau Titik Minimum suatu Fungsi Kuadratik dengan Kaedah Penyempurnaan Kuasa Dua

Langkah-langkah untuk menukarkan bentuk am fungsi kuadratik kepada bentuk penyempurnaan kuasa dua:

Bentuk am fungsi kuadratik: f (x) = ax² + bx + c

Bentuk penyempurnaan kuasa dua: f (x) = a (x + p)² + q.

Langkah 1: Pastikan pekali x² adalah 1, dan lakukan pemfaktoran jika pekali x² bukan 1.

Langkah 2: Tambah

+ {(\frac{pekali x}{2})}^{2} - {(\frac{pekali x}{2})}^{2}

Langkah 3: Menyempurnakan kuasa dua [tukar f (x) = ax² + bx + c kepada f (x) = a (x + p)²+ q].

Bab 3 Fungsi Kuadratik

Posted on May 20, 2016 by user

3.3a Lakaran Graf Fungsi Kuadratik (Contoh)

Contoh:

Ungkapkan y = 5 + 4x – x ² dalam bentuk y = a – (x + b )² , dengan a , b, dan c sebagai pemalar. Seterusnya, nyatakan nilai maksimum, y, dan nilai x. Lakarkan lengkung y = 5 + 4x – x ² .

Penyelesaian: