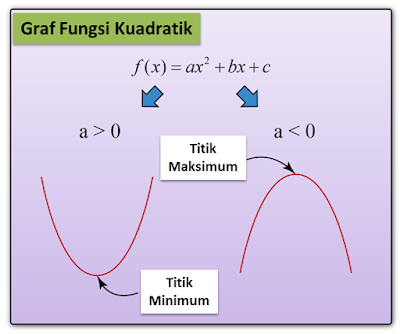
3.3 Lakaran Graf Fungsi Kuadratik
Langkah-langkah melakar graf fungsi kuadratik f (x
) = ax
2 + bx + c adalah seperti berikut:
(a) Tentukan nilai a untuk mengetahui bentuk graf.
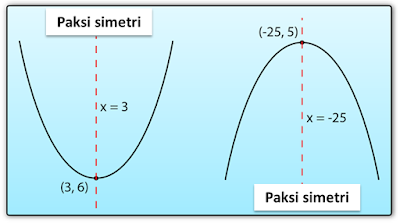
(b) Cari titik maksimum/minimum graf
(c) Cari pintasan paksi-x graf
(d) Cari pintasan paksi-y graf
Contoh:
Lakar graf bagi fungsi kuadratik f (x
) = x
2 – x – 12
Penyelesaian:
(a) Bentuk graf
Pekali x2 adalah positif, maka graf adalah berbentuk parabola U dengan satu titik minimum.
(b) Titik minimum graf
Dengan penyempurnaan kuasa dua
(c) Pintasan paksi-x, f (x
) = 0
0 = x
2 – x – 12
(x + 5) (x – 6) = 0
x = – 5 atau x = 6
(d) ) Pintasan paksi-y, x
= 0
f (0) = (0)2
– (0) – 12 = – 12