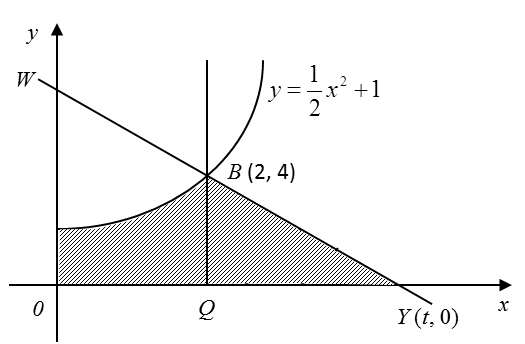
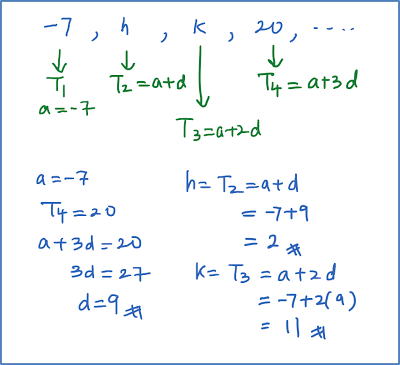
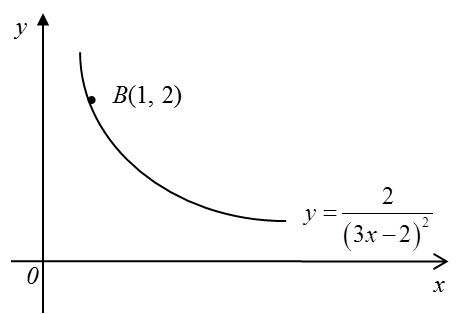3.8 Pengamiran, SPM Praktis (Kertas 2)
Soalan 3:
Fungsi kecerunan suatu lengkung melalui titik P(2, -14) ialah 6x2 – 12x.
Cari
(a)
persamaan lengkung itu,
(b)
koordinat titik-titik pusingan lengkung itu, dan tentukan sama ada setiap titik pusingan itu adalah maksimum atau minimum.
Penyelesaian:
(a)
Fungsi kecerunan suatu lengkung, dy/dx
= 6x2 – 12x
persamaan lengkung,
y = 2x3 – 6x2 + c
–14 = 2(2)3 – 6(2)2 + c, di titik P (2, –14)
–14 = –8 + c
c = –6
y = 2x3 – 6x2 – 6
(b)
dy/dx
= 6x2 – 12x
Di titik pusingan, dy/dx
= 0
6x2 – 12x = 0
6(x – 2) = 0
x = 0, x = 2
x = 0, y = 2(0)3 – 6(0)2 – 6 = –6
x = 2, y = 2(2)3 – 6(2)2 – 6 = –14