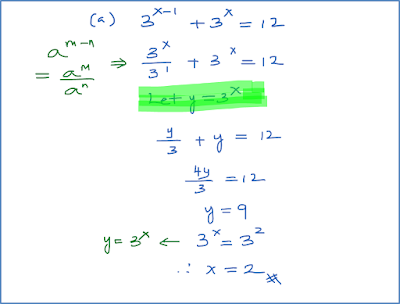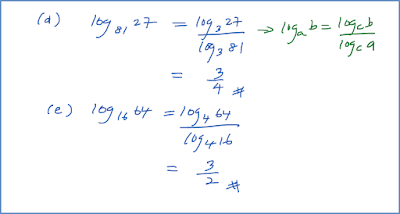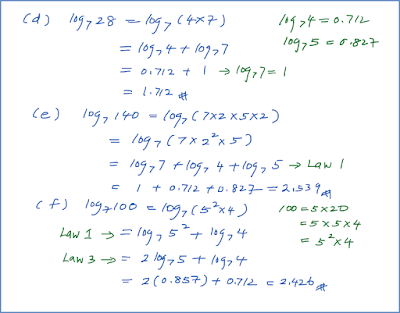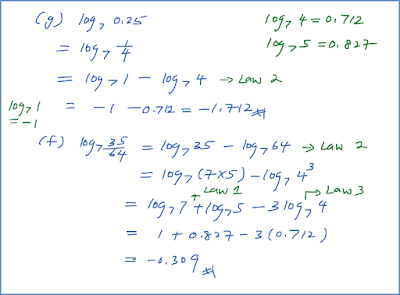5.3 Persamaan yang Melibatkan Indeks (Contoh Soalan)
Contoh 4 (Persamaan Indeks (Asas Sama) – Penggantian):
Selesaikan setiap persamaan yang berikut.
(a) 3x
−
1
+ 3x
= 12
(b) 2x + 2x + 3 = 72
(c) 4x + 1 + 22x = 20
(b) 2x + 2x + 3 = 72
(c) 4x + 1 + 22x = 20
Penyelesaian: