Soalan 4 (10 markah):
(a) Buktikan bahawa 2 tan x kos2 x = sin 2x.
(b) Seterusnya, selesaikan persamaan 4 tan x kos2 x = 1 untuk 0 ≤ x ≤ 2π.
(c)(i) Lakar graf y = sin 2x untuk 0 ≤ x ≤ 2π.
(c)(ii) Seterusnya, menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan 4π tan x kos2 x = x – 2π untuk 0 ≤ x ≤ 2π.
Nyatakan bilangan penyelesaian.
Penyelesaian:
(a)
2tanxkos2x=sin2xSebelah kiri=2tanxkos2x=2×sinxkosx×kos2x=2sinxkosx=sin2x= Sebelah kanan (Terbukti)
(b)
4tanxkos2x=1, 0≤x≤2π2(2tanxkos2x)=12sin2x=1sin2x=12Sudut asas=π62x=π6,(π−π6),(2π+π6),(3π−π6)2x=π6,5π6,13π6,17π6x=π12,5π12,13π12,17π12
(c)(i)
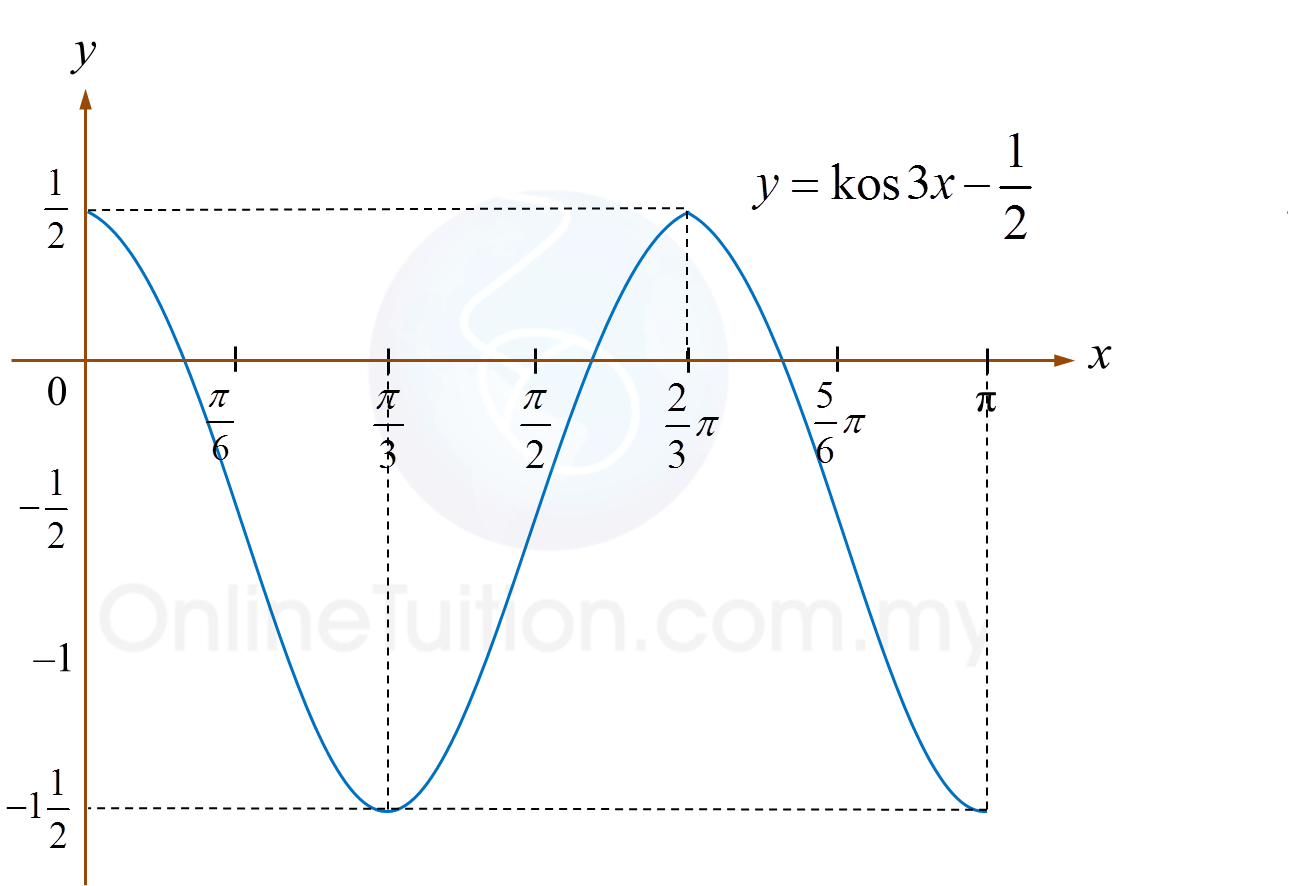
y = sin 2x, 0 ≤ x ≤ 2π.
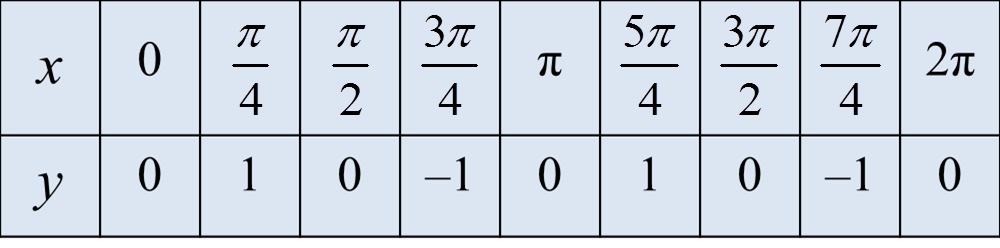
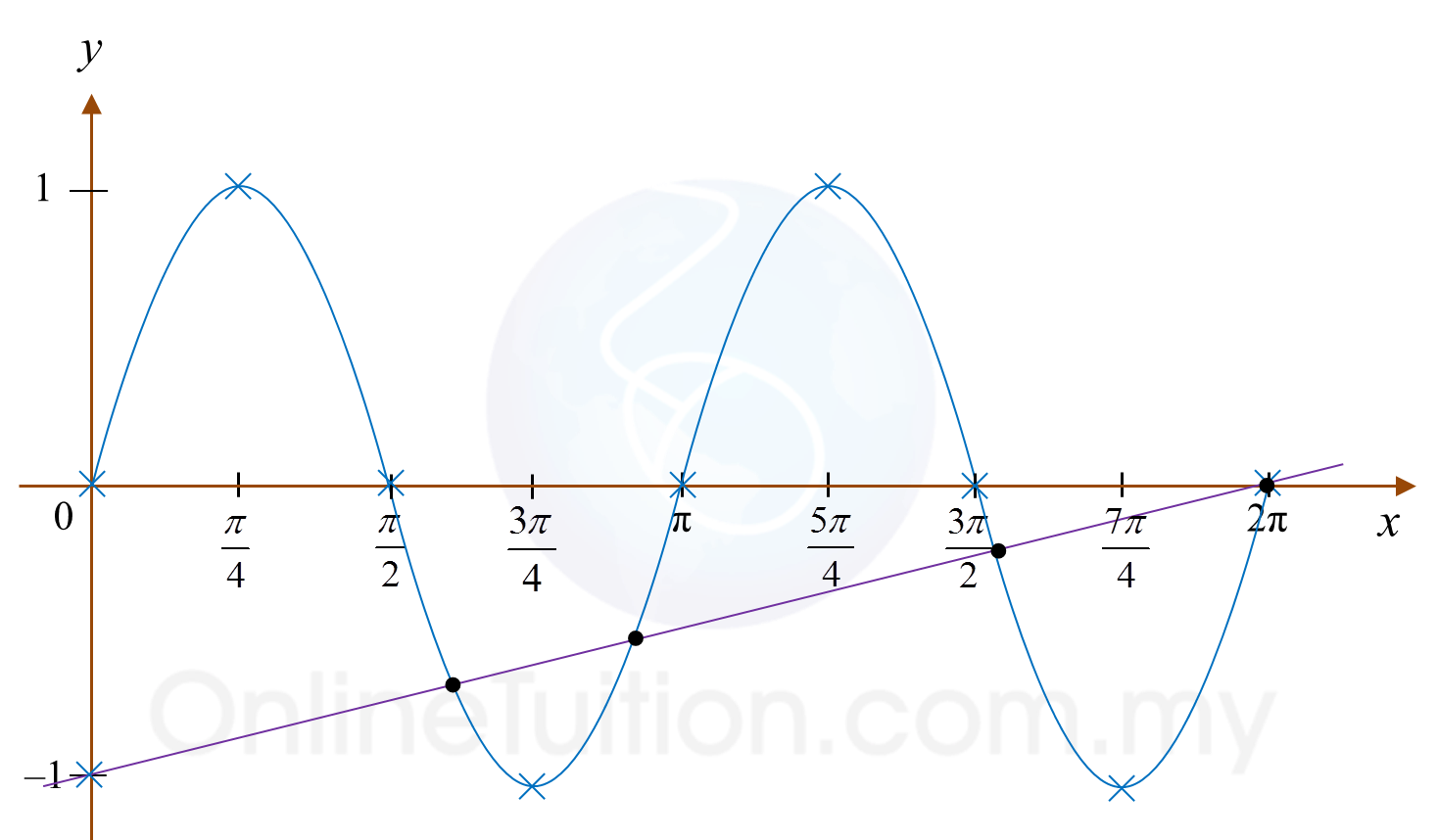
(c)(ii)
4πtanxkos2x=x−2π2π(2tanxkos2x)=x−2π2πsin2x=x−2πsin2x=x2π−2π2πsin2x=x2π−1y=x2π−1
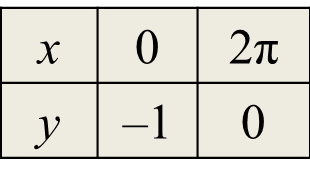
Bilangan penyelesaian = 4
(a) Buktikan bahawa 2 tan x kos2 x = sin 2x.
(b) Seterusnya, selesaikan persamaan 4 tan x kos2 x = 1 untuk 0 ≤ x ≤ 2π.
(c)(i) Lakar graf y = sin 2x untuk 0 ≤ x ≤ 2π.
(c)(ii) Seterusnya, menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan 4π tan x kos2 x = x – 2π untuk 0 ≤ x ≤ 2π.
Nyatakan bilangan penyelesaian.
Penyelesaian:
(a)
2tanxkos2x=sin2xSebelah kiri=2tanxkos2x=2×sinxkosx×kos2x=2sinxkosx=sin2x= Sebelah kanan (Terbukti)
(b)
4tanxkos2x=1, 0≤x≤2π2(2tanxkos2x)=12sin2x=1sin2x=12Sudut asas=π62x=π6,(π−π6),(2π+π6),(3π−π6)2x=π6,5π6,13π6,17π6x=π12,5π12,13π12,17π12

(c)(i)
y = sin 2x, 0 ≤ x ≤ 2π.


(c)(ii)
4πtanxkos2x=x−2π2π(2tanxkos2x)=x−2π2πsin2x=x−2πsin2x=x2π−2π2πsin2x=x2π−1y=x2π−1

Bilangan penyelesaian = 4


 Rajah 1
Rajah 1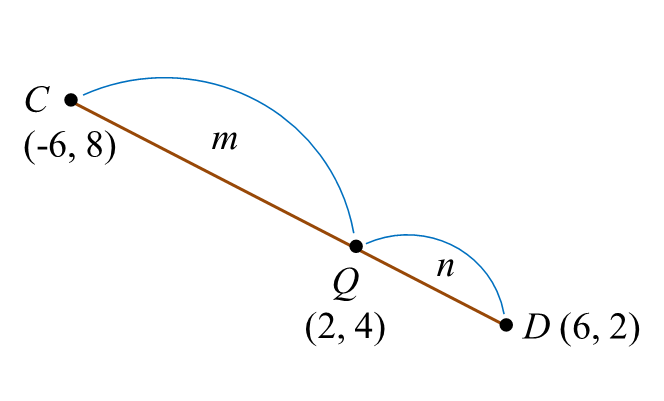
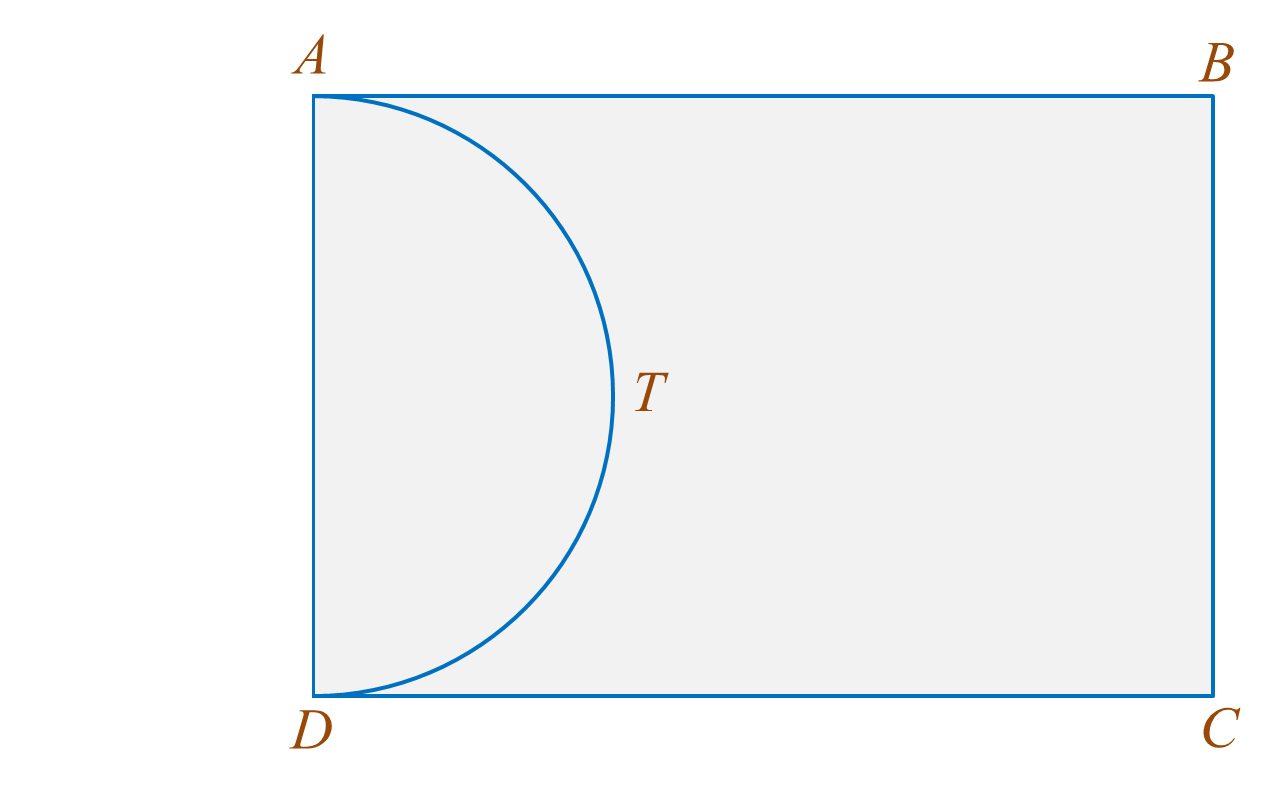 Diberi bahawa DC = 6y meter dan BC = 7x meter, x ≠ y. Luas taman berbentuk segi empat tepat ABCD ialah 168 meter2 dan perimeter kawasan berumput ialah 60 meter. Kolam dengan kedalaman seragam mengandungi 15.4 meter3 air.
Diberi bahawa DC = 6y meter dan BC = 7x meter, x ≠ y. Luas taman berbentuk segi empat tepat ABCD ialah 168 meter2 dan perimeter kawasan berumput ialah 60 meter. Kolam dengan kedalaman seragam mengandungi 15.4 meter3 air.
