Soalan 6 (7 markah):
Rajah menunjukkan sebahagian daripada dinding berbentuk segi empat tepat yang dicat dengan warna hijau, H, biru, B dan ungu, U secara berselang seli.
Tinggi dinding ialah 2 m. Panjang sisi segi empat tepat berwarna yang pertama ialah 5 cm dan panjang sisi bagi setiap segi empat tepat berwarna berikutnya bertambah sebanyak 3 cm.

Diberi bahawa jumlah segi empat tepat berwarna ialah 54.
(a) Cari
(i) panjang sisi, dalam cm, bagi segi empat tepat berwarna yang terakhir,
(ii) jumlah panjang, dalam cm, dinding yang dicat.
(b) Segi empat tepat berwarna yang ke berapa mempunyai keluasan 28000 cm2?
Seterusnya, nyatakan warna bagi segi empat tepat berkenaan.
Penyelesaian:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
= 164 cm
(ii)
Sn=n2(a+l)S54=542(5+164) =4563 cm
(b)
Luas bagi segi empat tepat pertama
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Luas bagi segi empat tepat kedua
= 200 × (5 + 3)
= 1600 cm
Luas bagi segi empat tepat ketiga
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
Warna bagi segi empat tepat berkenaan berwarna hijau.
Rajah menunjukkan sebahagian daripada dinding berbentuk segi empat tepat yang dicat dengan warna hijau, H, biru, B dan ungu, U secara berselang seli.
Tinggi dinding ialah 2 m. Panjang sisi segi empat tepat berwarna yang pertama ialah 5 cm dan panjang sisi bagi setiap segi empat tepat berwarna berikutnya bertambah sebanyak 3 cm.

Diberi bahawa jumlah segi empat tepat berwarna ialah 54.
(a) Cari
(i) panjang sisi, dalam cm, bagi segi empat tepat berwarna yang terakhir,
(ii) jumlah panjang, dalam cm, dinding yang dicat.
(b) Segi empat tepat berwarna yang ke berapa mempunyai keluasan 28000 cm2?
Seterusnya, nyatakan warna bagi segi empat tepat berkenaan.
Penyelesaian:
(a)
5, 8, 11, …
a = 5, d = 3
(i)
T54 = 1 + (54 – 1)d
= 5 + 53(3)
= 164 cm
(ii)
Sn=n2(a+l)S54=542(5+164) =4563 cm
(b)
Luas bagi segi empat tepat pertama
= 2 m × 5 cm
= 200 × 5
= 1000 cm
Luas bagi segi empat tepat kedua
= 200 × (5 + 3)
= 1600 cm
Luas bagi segi empat tepat ketiga
= 200 × (5 + 3 + 3)
= 2200 cm
1000, 1600, 2200, …
a = 1000, d = 600
Tn = 28 000
a + (n – 1)d = 28 000
1000 + (n – 1)600 = 28 000
600(n – 1) = 27 000
n – 1 = 45
n = 46
Warna bagi segi empat tepat berkenaan berwarna hijau.
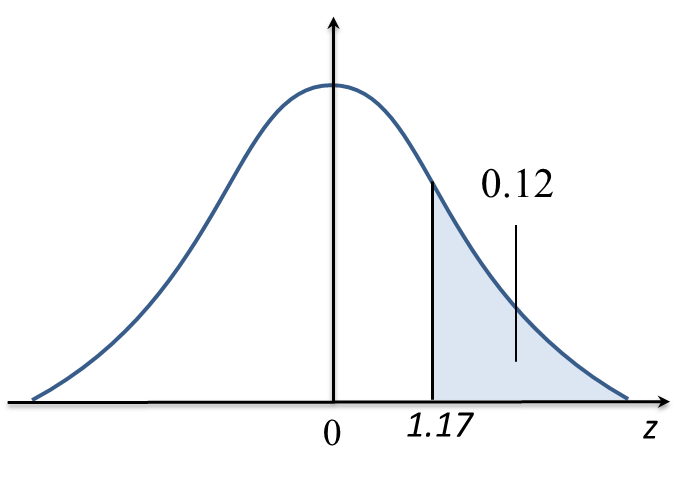 Oleh itu, markah minimum untuk mendapat gred A ialah 66.
Oleh itu, markah minimum untuk mendapat gred A ialah 66.