Soalan 5:
Rajah di bawah menunjukkan trapezium ABCD.
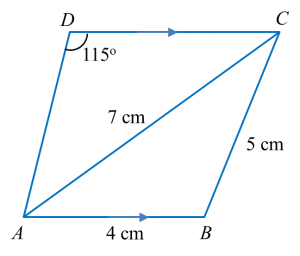 (a) Hitung
(a) Hitung
(i) ∠BAC.
(ii) panjang, dalam cm, bagi AD.
(b) Garis lurus AB dipanjangkan ke B’ dengan keadaan BC = B’C.
(i) Lakar trapezium AB’CD.
(ii) Hitung luas, dalam, cm2, bagi ∆BB’C.
Penyelesaian:
(a)(i)
52=42+72−2(4)(7)kos∠BAC25=16+49−56kos∠BAC56kos∠BAC=40kos∠BAC=4056 ∠BAC=kos−14056 =44o25'
(a)(ii)
(b)(i)
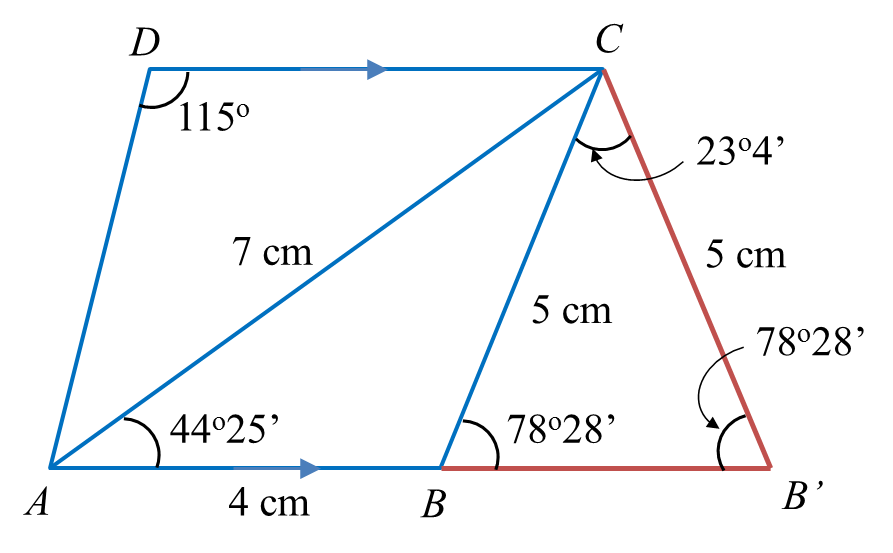
(b)(ii)
Rajah di bawah menunjukkan trapezium ABCD.
 (a) Hitung
(a) Hitung(i) ∠BAC.
(ii) panjang, dalam cm, bagi AD.
(b) Garis lurus AB dipanjangkan ke B’ dengan keadaan BC = B’C.
(i) Lakar trapezium AB’CD.
(ii) Hitung luas, dalam, cm2, bagi ∆BB’C.
Penyelesaian:
(a)(i)
52=42+72−2(4)(7)kos∠BAC25=16+49−56kos∠BAC56kos∠BAC=40kos∠BAC=4056 ∠BAC=kos−14056 =44o25'
(a)(ii)
(b)(i)

(b)(ii)



 [Guna π = 3.142]
[Guna π = 3.142]
 Jadual
Jadual Jadual
Jadual