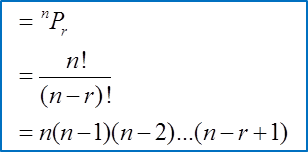Bab 17 Pilir Atur dan Gabungan

Posted on May 15, 2020 by Myhometuition

Soalan 8:

Dalam sebuah kotak terdapat 10 biji gula-gula yang berlainan perisa.

Cari

(a) Bilangan cara 3 biji gula-gula boleh dipilih dari kotak itu.

(b) Bilangan cara sekurang-kurangnya 8 biji gula-gula boleh dipilih dari kotak itu.

Penyelesaian:

(a)

Bilangan cara memilih 3 daripada 10 biji gula-gula

\begin{array}{l} =^{10} C_{3} \\ = 120 \end{array}

(b)

Bilangan cara memilih 8 biji gula-gula =

^{10} C_{8}

Bilangan cara memilih 9 biji gula-gula =

^{10} C_{9}

Bilangan cara memilih 10 biji gula-gula =

^{10} C_{10}

Oleh itu, bilangan cara sekurang-kurangnya 8 biji gula-gula boleh dipilih dari kotak

\begin{array}{l} =^{10} C_{8} +^{10} C_{9} +^{10} C_{10} \\ = 56 \end{array}

Soalan 9 (4 markah):
Danya mempunyai sebuah kedai barangan perhiasan rumah. Pada suatu hari, Danya menerima 14 set cawan daripada seorang pembekal. Setiap set mengandungi 6 biji cawan yang berlainan warna.

(a) Danya memilih 3 set cawan secara rawak untuk diperiksa.
Cari bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih set-set cawan itu.

(b) Danya mengambil satu set cawan untuk dipamerkan dengan menyusunnya secara sebaris.
Cari bilangan cara yang berlainan cawan-cawan itu boleh disusun dengan keadaan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah.

Penyelesaian:
(a)
Bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih 3 set cawan secara rawak untuk diperiksa
= ¹⁴C₃=364

(b)

Bilangan cara (Cawan berwarna biru diletak bersebelahan cawan berwarna merah)
= 5! × 2!
= 240

Bilangan cara yang berlainan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah
= 6! – 240
= 720 – 240
= 480

Soalan 10 (2 markah):

\begin{array}{l} (a) Diberi {}^{6}C_{n} > 1, senaraikan semua \\ nilai-nilai yang mungkin bagi n . \\ (b) Diberi {}^{y}C_{m} = {}^{y}C_{n}, ungkapkan y \\ dalam sebutan m dan n . \end{array}

Penyelesaian:
(a)
n = 1, 2, 3, 4, 5

(b)
y = m + n

Bab 17 Pilir Atur dan Gabungan

Posted on October 3, 2016 by user

6.1.2 Pilir Atur (Bahagian 2)

(C) Pilih Atur r Benda daripada n Benda

Jika n benda yang berlainan hendak disusun pada satu baris dengan melibatkan r benda pada sesuatu ketika, maka bilangan susunan atau pilihatur yang boleh dilakukan ialah,

Contoh 1:

Menilai setiap yang berikut:

{(a)}^{5} P_{2} {(b)}^{7} P_{3} {(c)}^{9} P_{4}

Penyelesaian:

\begin{array}{l} (a) \\ ^{5} P_{2} = \frac{5!}{(5 - 2)!} = \frac{5!}{3!} \\ = \frac{5 \times 4 \times 3!}{3!} = 5 \times 4 = 20 \end{array}

\begin{array}{l} b) \\ ^{7} P_{3} = \frac{7!}{(7 - 3)!} = \frac{7!}{4!} \\ = \frac{7 \times 6 \times 5 \times 4!}{4!} = 7 \times 6 \times 5 = 210 \end{array}

\begin{array}{l} (c) \\ ^{9} P_{4} = \frac{9!}{(9 - 4)!} = \frac{9!}{5!} \\ = \frac{9 \times 8 \times 7 \times 6 \times 5!}{5!} = 9 \times 8 \times 7 \times 6 = 3024 \end{array}

Gunakan Kalkulator:

Bab 17 Pilir Atur dan Gabungan

Posted on October 3, 2016 by user

Bab 6 Pilir Atur dan Gabungan

6.1.1 Pilir Atur (Bahagian 1)

(A) Prinsip Pendaraban

Jika suatu peristiwa A boleh berlaku dalam r cara dan suatu peristiwa B boleh berlaku dalam s cara, maka bilangan cara peristiwa A boleh berlaku diikuti dengan berlakunya peristiwa B ialah r × s cara yang berlainan.

Contoh 1:

Terdapat 3 jalan raya berlainan dari bandar P ke bandar Q dan 4 jalan raya berlainan dari bandar Q ke bandar R. Cari bilangan cara seorang pemandu teksi boleh memilih untuk mengangkut pelancong dari bandar P ke bandar R melalui bandar Q.

Penyelesaian:

3 × 4 = 12

(B) Pilih Atur

Contoh 2:

Hitungkan setiap yang berikut:

(a) 7!
(b) 4!6!
(c) 0!5!

\begin{array}{l} (d) \frac{7!}{5!} \\ (e) \frac{8!}{4!} \\ (f) \frac{n!}{(n - 2)!} \\ (g) \frac{n! 0!}{(n - 1)!} \\ (h) \frac{3! (n + 1)!}{2! n!} \end{array}

Penyelesaian:

(a) 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

(b) 4!6! = (4 × 3 × 2 × 1)( 6 × 5 × 4 × 3 × 2 × 1) = 17280

(c) 0!5! = (1)( 5 × 4 × 3 × 2 × 1) = 120

\begin{array}{l} (d) \frac{7!}{5!} = \frac{7 \times 6 \times 5!}{5!} = 7 \times 6 = 42 \\ (e) \frac{8!}{4!} = \frac{8 \times 7 \times 6 \times 5 \times 4!}{4!} = 8 \times 7 \times 6 \times 5 = 1680 \\ (f) \frac{n!}{(n - 2)!} = \frac{n (n - 1) (n - 2)}{(n - 2)} = n (n - 1) \\ (g) \frac{n! 0!}{(n - 1)!} = \frac{n (n - 1) (1)}{(n - 1)} = n \\ (h) \frac{3! (n + 1)!}{2! n!} = \frac{3 \times 2! (n + 1) (n) (n - 1)}{2! n (n - 1)} = 3 (n + 1) \end{array}

Gunakan Kalkulator:

Bab 17 Pilir Atur dan Gabungan

Posted on July 11, 2016 by user

6.2 Gabungan

1. Bilangan gabungan r objek daripada n objek

^{n} C_{r} = \frac{n!}{r! (n - r)!}

2. Bilangan gabungan r objek daripada n objek yang berlainan ialah bilangan pilihan r objek daripada n objek dengan tanpa mengambil kira tertib susunan.

\begin{array}{l} Peringatan: \\ (i)^{n} C_{0} = 1 \\ (i i)^{n} C_{n} = 1 \\ (i i i)^{n} C_{r} =^{n} C_{n - r} \end{array}

Contoh 1:

\begin{array}{l} {Hitung nilai}^{7} C_{2} \\ ^{7} C_{2} = \frac{7!}{(7 - 2)! \times 2!} \\ = \frac{7!}{5! \times 2!} \\ = \frac{7 \times 6 \times 5!}{5! \times 2!} \\ = \frac{7 \times 6}{2 \times 1} \\ = 21 \end{array}

Contoh 2:

6 biji guli yang mempunyai warna yang berbeza akan dibahagikan sama rata kepada 2 orang kanak-kanak. Cari bilangan cara pembahagian guli tersebut dapat dibuat.

Penyelesaian:

Bilangan cara memberi 3 biji guli kepada kanak-kanak pertama =

^{6} C_{3}

Bilangan cara memberi baki 3 biji guli kepada kanak-kanak kedua =

^{3} C_{3}

Bilangan cara pembahagian guli sama rata kepada 2 orang kanak-kanak

\begin{array}{l} =^{6} C_{3} \times^{3} C_{3} \\ = 20 \times 1 \\ = 20 \end{array}

Bab 17 Pilir Atur dan Gabungan

Posted on July 11, 2016 by user

6.3 Pilir Atur dan Gabungan, SPM praktis (Kertas 1)

Soalan 5:

Satu jawatankuasa yang terdiri daripada 6 orang ahli dipilih secara rawak daripada 5 orang guru dan 4 orang pelajar. Cari bilangan cara jawatankuasa itu boleh dibentuk jika

(a) tiada sebarang syarat dikenakan,

(b) bilangan guru lebih daripada bilangan pelajar.

Penyelesaian:

(a)

Jumlah ahli jawatankuasa = 5 + 4 = 9

6 orang ahli dipilih secara rawak daripada 9 orang dengan tiada sebarang syarat dikenakan

=^{9} C_{6} = 84

(b)

Jika bilangan guru mesti lebih daripada bilangan pelajar, gabungan adalah seperti berikut

= 4 orang guru 2 orang pelajar + 5 orang guru seorang pelajar

=^{5} C_{4} \times^{4} C_{2} +^{5} C_{5} \times^{4} C_{1}

= 30 + 4

= 34

Soalan 6:

Suatu jawatankuasa sekolah yang terdiri daripada enam orang dipilih secara rawak daripada 6 orang guru lelaki, 4 orang guru wanita dan seorang guru besar lelaki. Cari bilangan cara jawatankuasa itu boleh dibentuk jika

(a) guru besar adalah pengerusi jawatankuasa itu,

(b) jawatankuasa itu mengandungi tepat 2 orang guru wanita,

Penyelesaian:

(a)

Jika guru besar adalah pengerusi jawatankuasa, bilangan jawatankuasa yang tinggal terdiri daripada 5 ahli.

Maka, bilangan cara jawatankuasa itu boleh dibentuk daripada 6 orang guru lelaki dan 4 orang guru wanita

\begin{array}{l} =^{10} C_{5} \\ = 252 \end{array}

(b)

Tepat 2 orang guru wanita dalam jawatankuasa

\begin{array}{l} =^{4} C_{2} \times^{7} C_{4} \\ = 210 \end{array}

(c)

Jawatankuasa mengandungi bilangan guru lelaki yang tidak melebihi empat orang

= 4 orang guru lelaki 2 orang guru wanita + 3 orang guru lelaki 3 orang guru wanita + 2 orang guru lelaki 4 orang guru wanita

=^{7} C_{4} \times^{4} C_{2} +^{7} C_{3} \times^{4} C_{3} +^{7} C_{2} \times^{4} C_{4}

= 210 + 140 + 21

= 371

Soalan 7:

Jawatankuasa pengawas sebuah sekolah terdiri daripada 6 orang ahli dipilih secara rawak daripada 6 orang pelajar Melayu, 5 orang pelajar Cina dan 4 orang pelajar India. Cari bilangan cara jawatankuasa itu boleh dibentuk jika jawatankuasa itu mempunyai bilangan pelajar Melayu, Cina dan India yang sama.

Penyelesaian:

Bilangan cara jawatankuasa itu boleh dibentuk adalah terdiri daripada 2 pelajar Melayu, 2 pelajar Cina dan 2 pelajar India

\begin{array}{l} =^{6} C_{2} \times^{5} C_{2} \times^{4} C_{2} \\ = 900 \end{array}

Bab 17 Pilir Atur dan Gabungan

Posted on July 10, 2016 by user

6.3 Pilir Atur dan Gabungan, SPM praktis (Kertas 1)

Soalan 1:

Rajah di bawah menunjukkan lima keping kad huruf yang berlainan.

R E A C T

(a) Cari bilangan cara susunan yang mungkin, dalam satu baris, semua kad itu.

(b) Carikan bilangan cara susunan itu dengan keadaan huruf E dan huruf A adalah bersebelahan.

Penyelesaian:

(a)

Bilangan cara susunan yang mungkin = 5! = 120

(b)

Jika huruf Edan huruf A hendaklah disusun bersebelahan, EA dianggap sebagai satu unit.

Bersama-sama huruf-huruf ‘R’, ‘C’ dan ‘T’, kesemuanya 4 unit.

EA R C T

Bilangan cara susunan = 4!

Huruf ‘E’ dan ‘A’ boleh juga disusun antaranya dalam kumpulan sendiri.

Bilangan cara susunan = 2!

Oleh itu, bilangan cara susunan perkataan ‘REACT’ dengan keadaan huruf E dan huruf A adalah bersebelahan

= 4! × 2!

= 24 × 2

= 48

Soalan 2:

Sekumpulan 4 orang pelajar lelaki dan 3 orang pelajar perempuan akan duduk sebaris dalam suatu sesi mengambil gambar. Jika pelajar lelaki dan pelajar perempuan akan duduk secara alternatif (lelaki-perempuan-lelaki-perempuan…), hitung bilangan cara susunan itu boleh dibuat.

Penyelesaian:

Susunan 4 orang pelajar lelaki dan 3 orang pelajar perempuan duduk secara alternatif adalah berikut:

L P L P L P L

Bilangan cara menyusun tempat duduk untuk 4 pelajar lelaki = 4!

Bilangan cara menyusun tempat duduk untuk 3 pelajar perempuan = 3!

Oleh itu, bilangan cara untuk menyusun tempat duduk pelajar lelaki dan pelajar perempuan

= 4! × 3! = 144

Soalan 3:

Ahmad mempunyai 6 biji durian, 5 biji tembikai dan 2 biji betik. Jika dia ingin menyusun buah-buahan itu dalam satu baris dan buah-buahan yang sama jenis hendaklah dikumpul bersama, hitung bilangan cara susunan boleh dibuat. Saiz semua buah-buahan adalah berbeza.

Penyelesaian:

Bilangan cara menyusun buah-buahan yang sama jenis = 3!

DDDDDD TTTTT BB

Bilangan cara menyusun 6 biji durian = 6!

Bilangan cara menyusun 5 biji tembikai = 5!

Bilangan cara menyusun 2 biji betik = 2!

Oleh itu, bilangan cara menyusun jenis buah-buahan yang sama dalam sebaris

= 3! × 6! × 5! × 2!

= 1036800

Soalan 4:

Cari bilangan susunan yang dapat diperoleh, tanpa ulangan, daripada perkataan `SOMETHING' dengan syarat huruf pertama ialah huruf vokal.

Penyelesaian:

Huruf pertama boleh diisi oleh mana-mana huruf vokal O, E atau I =

^{3} P_{1}

Susunan bagi huruf-huruf yang seterusnya = 7!

Oleh itu, bilangan susunan bagi perkataan `SOMETHING' yang huruf pertama ialah huruf vocal

\begin{array}{l} =^{3} P_{1} \times 7! \\ = 15120 \end{array}