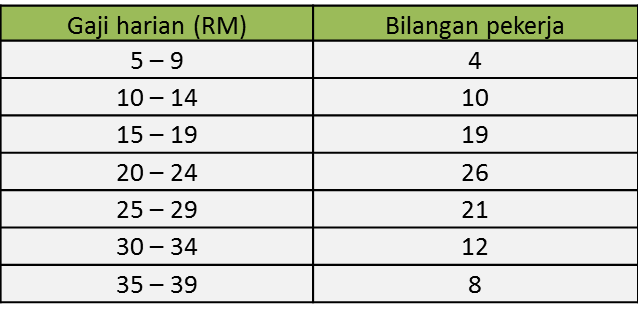
Soalan 10 (4 markah):
Satu set data terdiri daripada 2, 3, 4, 5 dan 6. Setiap nombor didarab dengan m dan ditambah dengan n, dengan keadaan m dan n adalah integer. Diberi bahawa min baharu ialah 17 dan sisihan piawai baharu ialah 4.242.
Cari nilai m dan nilai n.
Penyelesaian:
∑x=2+3+4+5+6=20∑x2=22+32+42+52+62=90Min=205=4Sisihan piawai=∑x2n−(ˉx)2 =905−42=2Min baharu=174m+n=17 .......... (1)Sisihan piawai baharu=4.242m×√2=4.242m=4.242√2=2.9995≈3Gantikan m=3 ke dalam (1):4(3)+n=17n=5
Satu set data terdiri daripada 2, 3, 4, 5 dan 6. Setiap nombor didarab dengan m dan ditambah dengan n, dengan keadaan m dan n adalah integer. Diberi bahawa min baharu ialah 17 dan sisihan piawai baharu ialah 4.242.
Cari nilai m dan nilai n.
Penyelesaian:
∑x=2+3+4+5+6=20∑x2=22+32+42+52+62=90Min=205=4Sisihan piawai=∑x2n−(ˉx)2 =905−42=2Min baharu=174m+n=17 .......... (1)Sisihan piawai baharu=4.242m×√2=4.242m=4.242√2=2.9995≈3Gantikan m=3 ke dalam (1):4(3)+n=17n=5
Soalan 11 (4 markah):
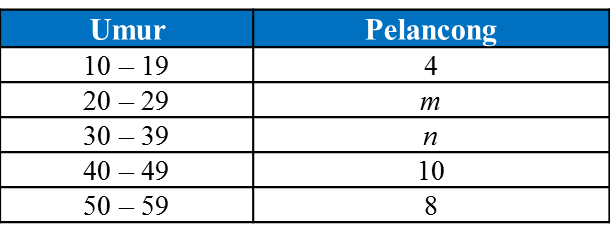
Jadual menunjukkan taburan markah bagi 40 orang murid dalam ujian Matematik Tambahan. Bilangan murid bagi selang kelas 40 – 59 tidak dinyatakan.
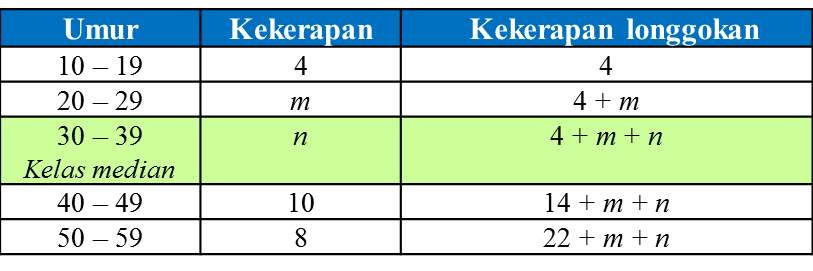
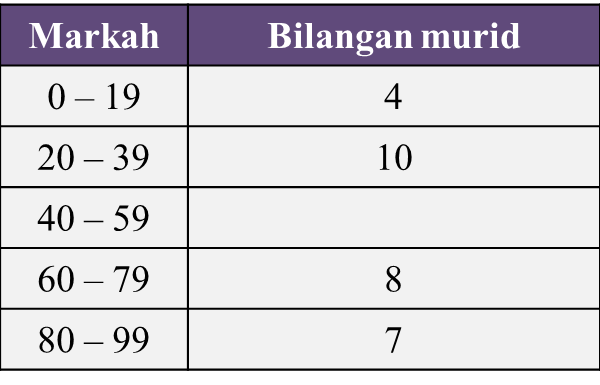 Jadual
Jadual
(a) Nyatakan kelas mod.
(b) Puan Zainon, guru mata pelajaran, berhasrat untuk memberi ganjaran kepada sepuluh murid terbaik. Murid-murid yang mencapai markah minimum dalam kedudukan sepuluh terbaik akan dipertimbangkan untuk menerima ganjaran tersebut. Elina memperoleh 74 markah.
Adakah Elina layak dipertimbangkan untuk menerima ganjaran itu? Beri sebab anda.
Penyelesaian:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Kelas mod = 40 – 59
(b)
Kedudukan sepuluh terbaik adalahT31, T32, T33, ... T40T31=59.5+58(79.5−59.5) =59.5+12.5 =72Murid perlu mencapai markah minimum 72.Elina layak dipertimbangkan untuk menerimaganjaran sebab markahnya > 72.
Jadual menunjukkan taburan markah bagi 40 orang murid dalam ujian Matematik Tambahan. Bilangan murid bagi selang kelas 40 – 59 tidak dinyatakan.
 Jadual
Jadual(a) Nyatakan kelas mod.
(b) Puan Zainon, guru mata pelajaran, berhasrat untuk memberi ganjaran kepada sepuluh murid terbaik. Murid-murid yang mencapai markah minimum dalam kedudukan sepuluh terbaik akan dipertimbangkan untuk menerima ganjaran tersebut. Elina memperoleh 74 markah.
Adakah Elina layak dipertimbangkan untuk menerima ganjaran itu? Beri sebab anda.
Penyelesaian:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Kelas mod = 40 – 59
(b)
Kedudukan sepuluh terbaik adalahT31, T32, T33, ... T40T31=59.5+58(79.5−59.5) =59.5+12.5 =72Murid perlu mencapai markah minimum 72.Elina layak dipertimbangkan untuk menerimaganjaran sebab markahnya > 72.
 Jadual
Jadual Jadual
Jadual