Soalan 7 (4 markah):
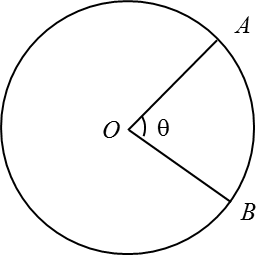
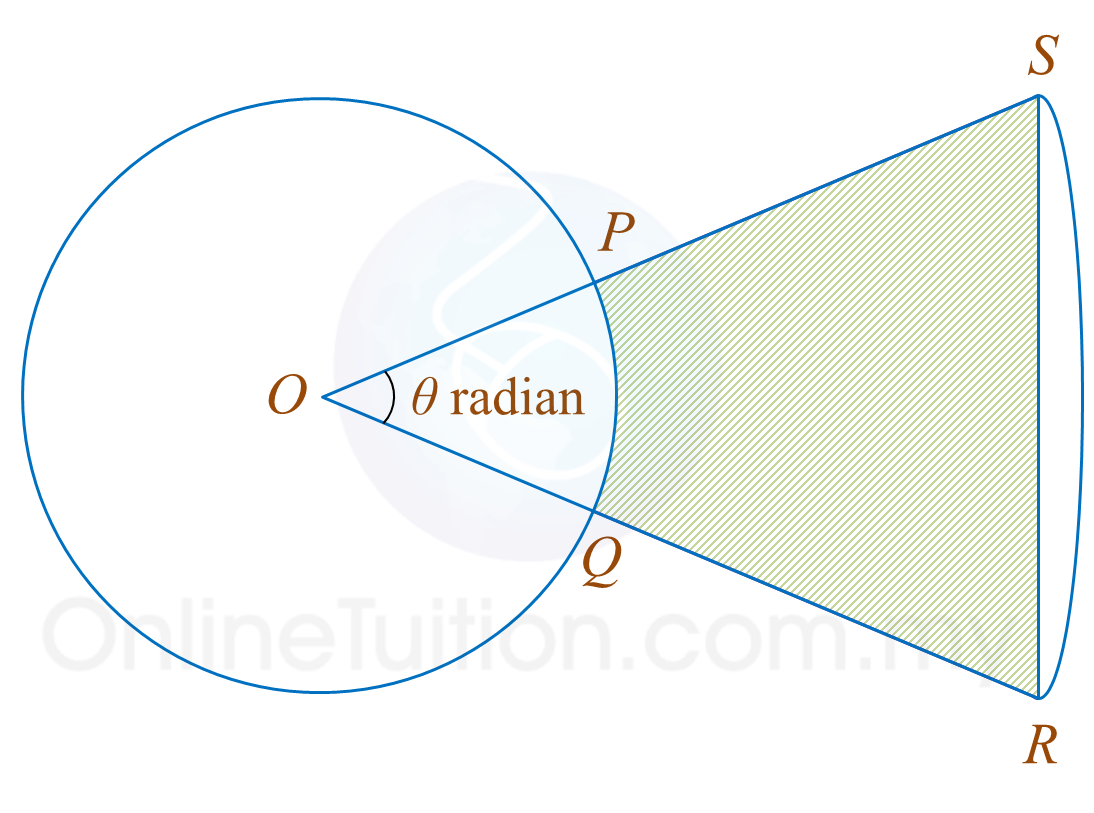
Rajah menunjukkan sebuah bulatan dengan pusat O.
 Rajah
Rajah
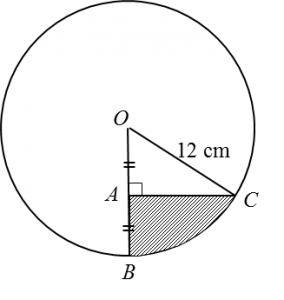
PR dan QR masing-masing adalah tangen kepada bulatan itu pada titik P dan titik Q. Diberi bahawa panjang lengkok PQ ialah 4 cm dan OR=5α cm.
Ungkapkan dalam sebutan α,
(a) jejari, r, bulatan itu,
(b) luas, A, kawasan berlorek.
Penyelesaian:
(a)
Diberi sPQ=4 rα=4 r=4α cm
(b)
PR=√(5α)2−(4α)2PR=√9α2PR=3αA= Luas kawasan berlorekA= Luas segi empat OPRQ− Luas sektor OPQ=2(Luas △ OPR)−12r2θ=2[12×3α×4α]−[12×(4α)2×α]=12α2−8α=12−8αα2 cm2
Rajah menunjukkan sebuah bulatan dengan pusat O.
 Rajah
Rajah PR dan QR masing-masing adalah tangen kepada bulatan itu pada titik P dan titik Q. Diberi bahawa panjang lengkok PQ ialah 4 cm dan OR=5α cm.
Ungkapkan dalam sebutan α,
(a) jejari, r, bulatan itu,
(b) luas, A, kawasan berlorek.
Penyelesaian:
(a)
Diberi sPQ=4 rα=4 r=4α cm
(b)
PR=√(5α)2−(4α)2PR=√9α2PR=3αA= Luas kawasan berlorekA= Luas segi empat OPRQ− Luas sektor OPQ=2(Luas △ OPR)−12r2θ=2[12×3α×4α]−[12×(4α)2×α]=12α2−8α=12−8αα2 cm2
Soalan 8 (3 markah):
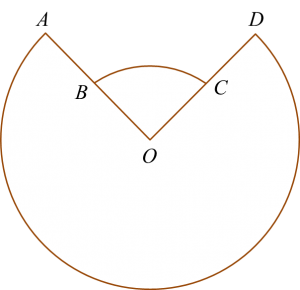
Rajah menunjukkan dua buah sektor AOD dan BOC bagi dua bulatan dengan pusat sepunya O.
 Rajah
Rajah
Sudut yang dicangkum pada pusat O oleh lengkok major AD ialah 7α radian dan perimeter seluruh rajah ialah 50 cm.
Diberi OB = r cm, OA = 2OB dan ∠BOC = 2α, ungkapkan r dalam sebutan α.
Penyelesaian:
Panjang lengkok major AOD=2r×7α=14rαPanjang lengkok minor BOC=r×2α=2rαPerimeter seluruh rajah=50 cm14rα+2rα+r+r=5016rα+2r=508rα+r=25r(8α+1)=25r=258α+1
Rajah menunjukkan dua buah sektor AOD dan BOC bagi dua bulatan dengan pusat sepunya O.
 Rajah
RajahSudut yang dicangkum pada pusat O oleh lengkok major AD ialah 7α radian dan perimeter seluruh rajah ialah 50 cm.
Diberi OB = r cm, OA = 2OB dan ∠BOC = 2α, ungkapkan r dalam sebutan α.
Penyelesaian:
Panjang lengkok major AOD=2r×7α=14rαPanjang lengkok minor BOC=r×2α=2rαPerimeter seluruh rajah=50 cm14rα+2rα+r+r=5016rα+2r=508rα+r=25r(8α+1)=25r=258α+1





 [Guna π = 3.142]
[Guna π = 3.142]