Vektor

4.6.2 Vektor, SPM Praktis (Kertas 1)

Soalan 3:

Rajah di bawah menunjukkan sebuah segi empat tepat OABC dan titik D terletak pada garis lurus OB.

Diberi bahawa OD = 3DB. Ungkapkan

\vec{O D}

, dalam sebutan

\underset{˜}{x} dan \underset{˜}{y} .

Penyelesaian:

\begin{array}{l} \vec{O B} = \vec{O A} + \vec{A B} = 3 \underset{˜}{x} + 12 \underset{˜}{y} \\ \vec{O D} = 3 \vec{D B} \\ \frac{\vec{O D}}{\vec{D B}} = \frac{3}{1} \\ \vec{O D} : \vec{D B} = 3 : 1 \\ ∴ \vec{O D} = \frac{3}{4} \vec{O B} \\ = \frac{3}{4} (3 \underset{˜}{x} + 12 \underset{˜}{y}) \\ = \frac{9}{4} \underset{˜}{x} + 9 \underset{˜}{y} \end{array}

Soalan 4:

Rajah di bawah menunjukkan sebuah segi empat selari ABCD dan BED ialah satu garis lurus.

\begin{array}{l} Diberi bahawa \vec{A B} = 7 \underset{˜}{p}, \vec{A D} = 5 \underset{˜}{q} dan D E = 3 E B, \\ ungkap dalam sebutan \underset{˜}{p} dan \underset{˜}{q} . \\ (a) \vec{B D} \\ (b) \vec{E C} \end{array}

Penyelesaian:

(a)

\begin{array}{l} Bagi segi empat selari, \\ \vec{A B} = \vec{D C} = 7 \underset{˜}{p}, \vec{A D} = \vec{B C} = 5 \underset{˜}{q} . \\ \vec{B D} = \vec{B A} + \vec{A D} \\ \vec{B D} = - 7 \underset{˜}{p} + 5 \underset{˜}{q} \end{array}

(b)

\begin{array}{l} \vec{D E} =3 \vec{E B} \\ \frac{\vec{E B}}{\vec{D E}} = \frac{1}{3} \to E B : D E = 1 : 3 \\ ∴ \vec{E B} = \frac{1}{4} \vec{D B} \\ = \frac{1}{4} (- \vec{B D}) \\ = \frac{1}{4} [- (- 7 \underset{˜}{p} + 5 \underset{˜}{q})] \leftarrow Dari (a) \\ = \frac{7}{4} \underset{˜}{p} + \frac{5}{4} \underset{˜}{q} \end{array}

\begin{array}{l} \vec{E C} = \vec{E B} + \vec{B C} \\ \vec{E C} = \frac{7}{4} \underset{˜}{p} + \frac{5}{4} \underset{˜}{q} + 5 \underset{˜}{q} \\ \vec{E C} = \frac{7}{4} \underset{˜}{p} + \frac{25}{4} \underset{˜}{q} \end{array}

4.6 Vektor, SPM Praktis (Kertas 1)

Soalan 1:

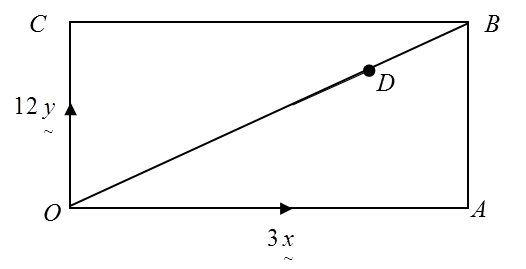
Diberi bahawa O (0, 0), A(–3, 4) dan B(-9, 12), Cari dalam sebutan vektor unit

\underset{˜}{i} dan \underset{˜}{j}

(a)

\vec{A B}

(b) vektor unit dalam arah

\vec{A B}

Penyelesaian:

(a)

\begin{array}{l} A = (- 3, 4), dengan itu \vec{O A} = - 3 \underset{˜}{i} + 4 \underset{˜}{j} \\ B = (- 9, 12), dengan itu \vec{O B} = - 9 \underset{˜}{i} + 12 \underset{˜}{j} \\ \vec{A B} = \vec{A O} + \vec{O B} \\ \vec{A B} = - (- 3 \underset{˜}{i} + 4 \underset{˜}{j}) + (- 9 \underset{˜}{i} + 12 \underset{˜}{j}) \\ \vec{A B} = 3 \underset{˜}{i} - 4 \underset{˜}{j} - 9 \underset{˜}{i} + 12 \underset{˜}{j} \\ \vec{A B} = - 6 \underset{˜}{i} + 8 \underset{˜}{j} \end{array}

(b)

\begin{array}{l} Magnitud | \vec{A B} |, \\ | \vec{A B} | = \sqrt{{(- 6)}^{2} + {(8)}^{2}} = 10 \\ Maka vektor unit dalam arah \vec{A B}, \\ \frac{\vec{A B}}{| \vec{A B} |} = \frac{1}{10} (- 6 \underset{˜}{i} + 8 \underset{˜}{j}) = - \frac{3}{5} \underset{˜}{i} + \frac{4}{5} \underset{˜}{j} \end{array}

Soalan 2:

Diberi bahawa A(–3, 2), B(4, 6) dan C(m, n), cari nilai m dan n supaya

2 \vec{A B} + \vec{B C} = (\begin{matrix} 12 \\ - 3 \end{matrix}) .

Penyelesaian:

\begin{array}{l} A = (\begin{array}{l} - 3 \\ 2 \end{array}), B = (\begin{array}{l} 4 \\ 6 \end{array}) and C = (\begin{array}{l} m \\ n \end{array}) \\ \vec{A B} = \vec{A O} + \vec{O B} \\ \vec{A B} = - (\begin{array}{l} - 3 \\ 2 \end{array}) + (\begin{array}{l} 4 \\ 6 \end{array}) = (\begin{array}{l} 7 \\ 4 \end{array}) \\ \vec{B C} = \vec{B O} + \vec{O C} \\ \vec{B C} = - (\begin{array}{l} 4 \\ 6 \end{array}) + (\begin{array}{l} m \\ n \end{array}) = (\begin{array}{l} - 4 + m \\ - 6 + n \end{array}) \end{array}

\begin{array}{l} Given 2 \vec{A B} + \vec{B C} = (\begin{matrix} 12 \\ - 3 \end{matrix}) \\ 2 (\begin{array}{l} 7 \\ 4 \end{array}) + (\begin{array}{l} - 4 + m \\ - 6 + n \end{array}) = (\begin{matrix} 12 \\ - 3 \end{matrix}) \\ (\begin{array}{l} 14 - 4 + m \\ 8 - 6 + n \end{array}) = (\begin{matrix} 12 \\ - 3 \end{matrix}) \end{array}

10 + m = 12

m= 2

2 + n = –3

n= –5

Bab 15 Vektor