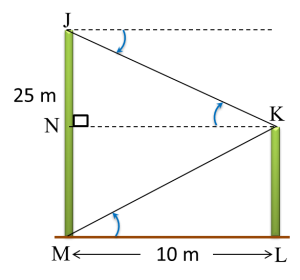
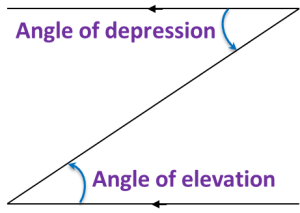
3. The angle of elevation or angle of depression is always measured from the horizontal line.

Example 3:
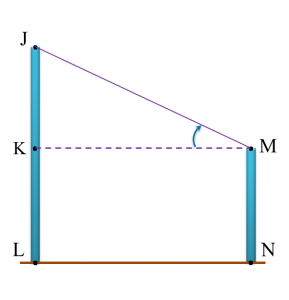
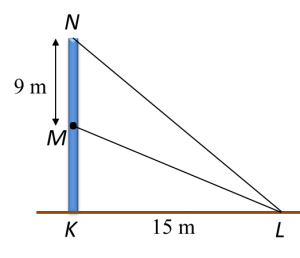
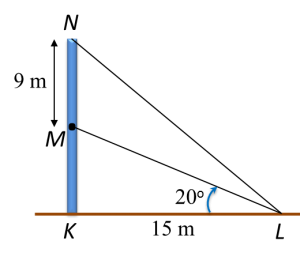
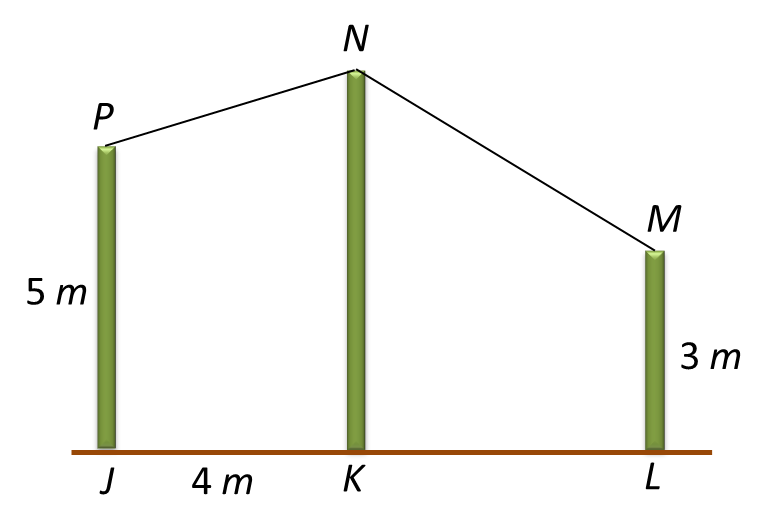
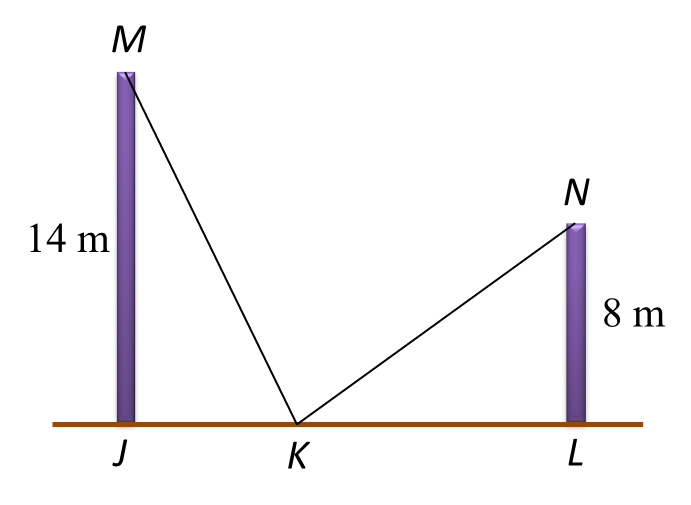
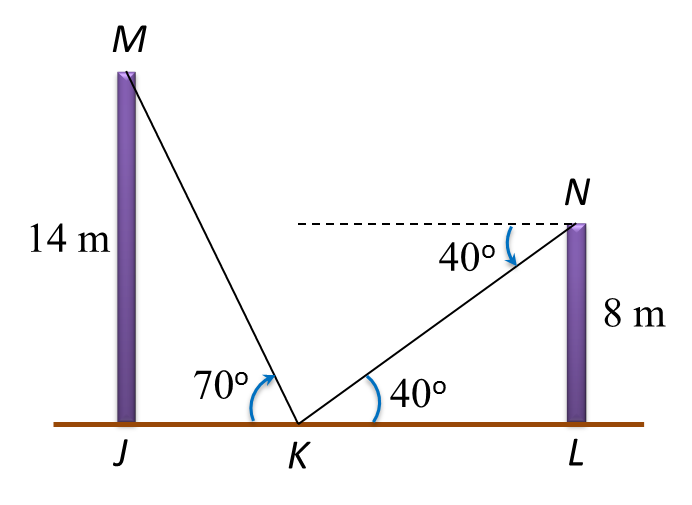
Diagram below shows two vertical poles JK and NL on a horizontal plane. M is a point on NL such that JK = ML.
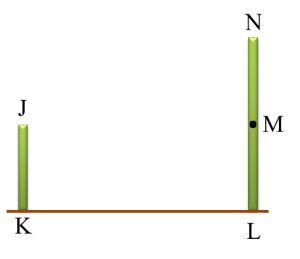

The angle of depression of point J from point N is
Solution:
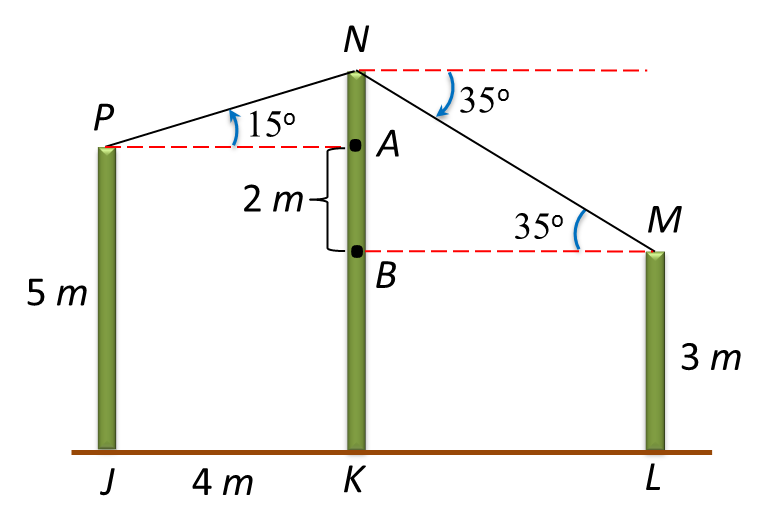
The angle of depression of point J from N is the angle between line JN and the horizontal line through N.
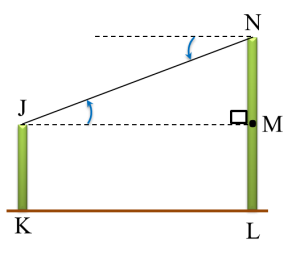

Angle of depression of J from N
= angle of elevation of N from J
=∠NJM
=∠NJM