8.3 Common Tangents (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

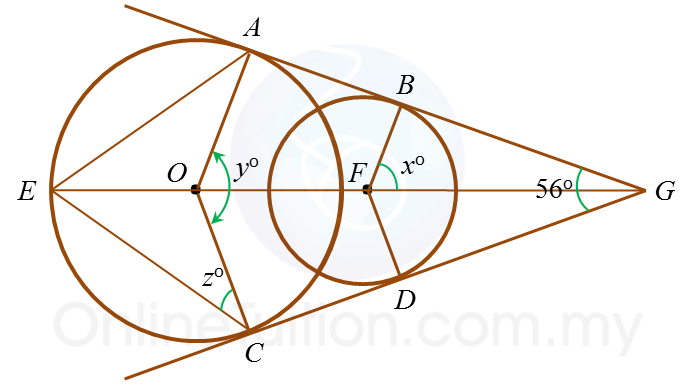
In the diagram, ABG and CDG are two common tangents to the circle with centres O and F respectively. Find the values of

(a) x, (b) y, (c) z.

Solution:

(a)

In ∆ BFG,

angle BFG = ½ × 56^o = 28^o

angle FBG = 90^o ← (tangent is 90^o to radius)

x^o+ 28^o + 90^o = 180^o

x^o= 180^o – 118^o

x^o= 62^o

x = 62

(b)

angle AOF = x^o = 62^o← (AO// BF)

y^o= 2 × 62^o

y^o= 124^o

y = 124

(c)

Exterior angle of AOC = 360^o – 124^o = 236^o

Angle EOC = ½ × 236^o = 118^o

z^o= (180^o – 118^o) × ½ ← (∆ EOC is isosceles triangle, angle OEC = angle OCE)

z^o= 31^o

z = 31

SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

In figure above, ABCD is a tangent to the circle CEF at point C. EGC is a straight line. The value of y is

Solution:

\begin{array}{l} ∠ C E F = ∠ D C F = 70^{\circ} \\ ∠ A E G + 70^{\circ} + 210^{\circ} = 360^{\circ} \\ ∠ A E G = 80^{\circ} \\ In cyclic quadrilateral A B G E, \\ ∠ A B G + ∠ A E G = 180^{\circ} \\ y^{\circ} + 80^{\circ} = 180^{\circ} \\ y = 100 \end{array}

Question 5:

In figure above, PAQ is a tangent to the circle at point A. AEC and BED are straight lines. The value of y is

Solution:

∠ABD = ∠ACD = 40^o

∠ACB = ∠PAB = 60^o

y= 180^o– ∠ACB – ∠CBD – ∠ABD

y= 180^o– 60^o – 25^o– 40^o = 55^o

Question 6:

In figure above, KPL is a tangent to the circle PQRS at point P. The value of x is

Solution:

∠PQS = ∠SPL= 55^o

∠SPQ = 180^o– 30^o – 55^o= 95^o

In cyclic quadrilateral,

∠SPQ + ∠SRQ = 180^o

95^o+ x^o = 180^o

x = 85^o

8.3 Common Tangents (Part 1)

Posted on April 23, 2020 by user

8.3 Common Tangents

A common tangent to two circles is a straight line that touches each of the circles at only one point.

1. Intersect at two points

(a) Circles of the same size

Number of common tangents	Properties of common tangents
Two common tangents: AB and CD	AC = BD AB = CD AB parallel to // OR parallel to // CD

(b) Circles of different sizes

Number of common tangents	Properties of common tangents
Two common tangents: ABE and CDE	AB = CD BE = DE OA // RB OC // RD