Graphs of Functions II
2.5 SPM Practice (Long Questions)
Question 6:
(a) Complete the table in the answer space for the equation y=36x by writing down the values of y when x = 3 and x = 8.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 1 cm to 1 unit on the x-axis and 1 cm to 1 unit on the y-axis, draw the graph of y=36x for 2 ≤ x ≤ 14.
(c) From your graph, find
(i) the value of y when x = 2.6,
(ii) the value of x when y = 4.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation 36x+x−14=0 for 2 ≤ x ≤ 14.
Answer:
Solution:
(a)
y=36xwhen x=3y=363=12when x=8y=368=4.5
(b)
(c)
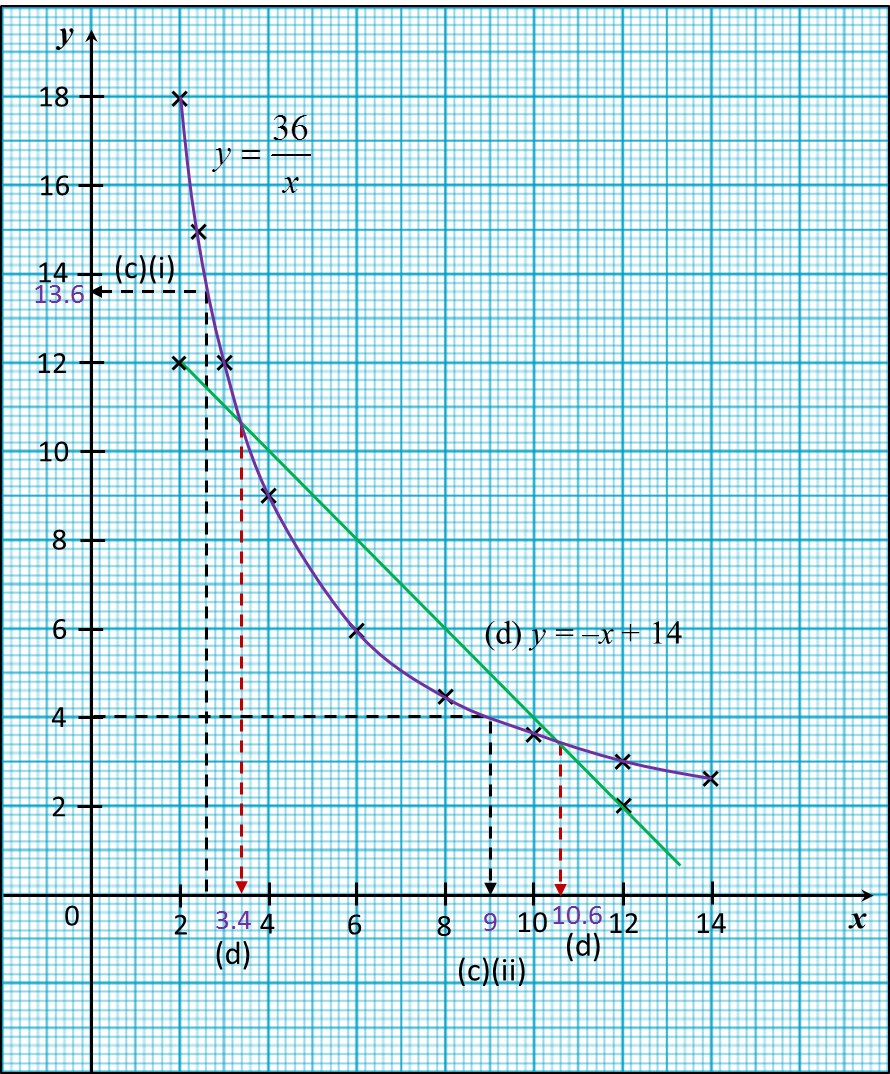
(i) From the graph, when x = 2.6, y = 13.6
(ii) From the graph, when y = 4, x = 9
(d)
y=36x ........... (1)0=36x+x−14 ........... (2)(1)−(2):y=−x+14
The suitable straight line is y = –x + 14.
From the graph, x = 3.4, 10.6.
(a) Complete the table in the answer space for the equation y=36x by writing down the values of y when x = 3 and x = 8.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 1 cm to 1 unit on the x-axis and 1 cm to 1 unit on the y-axis, draw the graph of y=36x for 2 ≤ x ≤ 14.
(c) From your graph, find
(i) the value of y when x = 2.6,
(ii) the value of x when y = 4.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation 36x+x−14=0 for 2 ≤ x ≤ 14.
Answer:
x |
2 |
2.4 |
3 |
4 |
6 |
8 |
10 |
12 |
14 |
y |
18 |
15 |
9 |
6 |
3.6 |
3 |
2.6 |
Solution:
(a)
y=36xwhen x=3y=363=12when x=8y=368=4.5
(b)

(c)
(i) From the graph, when x = 2.6, y = 13.6
(ii) From the graph, when y = 4, x = 9
(d)
y=36x ........... (1)0=36x+x−14 ........... (2)(1)−(2):y=−x+14
The suitable straight line is y = –x + 14.
x |
2 |
12 |
y = –x + 14 |
12 |
2
|
2.5 SPM Practice (Long Questions)
Question 5:
Solution:
(b)
(c)
(d)
y=24x-------------- (1)2x2+5x=24------ (2)(2)÷x,2x+5=24x-------- (3)(1)−(3),y−(2x+5)=0y=2x+5
The suitable straight line is y = 2x + 5.
(a) The following table shows the corresponding values of x and y for the equation
y=24x
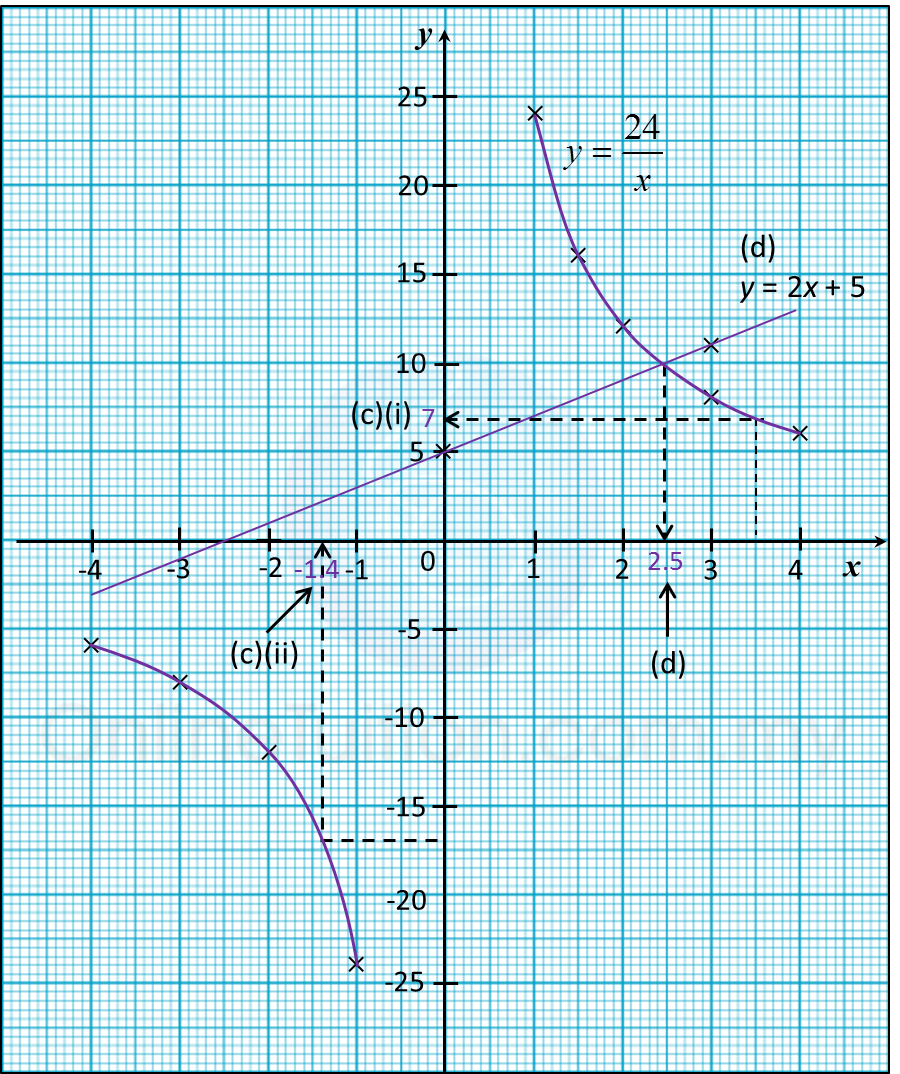
x |
–4 |
–3 |
–2 |
–1 |
1 |
1.5 |
2 |
3 |
4 |
y |
–6 |
k |
–12 |
–24 |
24 |
n |
12 |
8 |
6 |
Calculate the value of k and n.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of
y=24x
for –4 ≤ x ≤ 4.
(c) From your graph, find
(i) The value of y when x = 3.5,
(ii) The value of x when y = –17.
(d) Draw a suitable straight line on your graph to find the value of x which satisfy the equation 2x2 + 5x = 24 for –4 ≤ x ≤ 4.
(a)
y=24xwhen x=−3,k=24−3=−8when x=1.5,n=241.5=16
y=24xwhen x=−3,k=24−3=−8when x=1.5,n=241.5=16
(b)

(c)
(i) From the graph, when x = 3.5, y = 7
(ii) From the graph, when y = –17, x = –1.4
(d)
y=24x-------------- (1)2x2+5x=24------ (2)(2)÷x,2x+5=24x-------- (3)(1)−(3),y−(2x+5)=0y=2x+5
The suitable straight line is y = 2x + 5.
Determine the x-coordinate of the point of intersection of the curve and the straight line y = 2x + 5.
x |
0 |
3 |
y = 2x + 5 |
5 |
11 |
From the graph, x = 2.5
2.4 SPM Practice (Short Questions)
2.4 SPM Practice (Short Questions)
Question 1:
Which of the following graphs represent y = –x2 – x + 2?




Solution:
1. The coefficient of x2 < 0, its shape is ∩.
2. Find the x-intercepts by substituting y = 0 into the function.
y = –x2 –x + 2
when y = 0
0 = (–x + 1) (x + 2)
x = 1, –2
The answer is A.
Question 2:
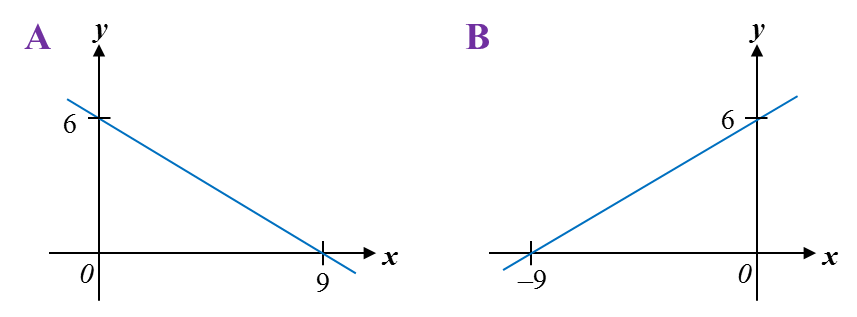
Which of the following graphs represent 3y = 18 + 2x?



Solution:
1. The highest power of x = 1, it is a linear graph, i.e. a straight line.
2. The coefficient of x > 0, the straight line is /.
3y = 18 + 2x
On the y-axis, x = 0.
3y = 18
y = 6
On the x-axis, y = 0.
0 = 18 + 2x
2x = –18
x = –9
The answer is B.
2.2 Solving Equations Graphically
2.2 Solving equations graphically
The solution of the equation f (x) = g (x) can be solved by graphical method.
Step 1: Draw the graphs of y = f (x) and y = g (x) on the same axes.
Step 2: The points of intersection of the graphs are the solutions of the equation f (x) = g(x). Read the values of x from the graph.
Solution of an Equation by Graphical Method
Example 1:
(c) From your graph, find
Solution:
(b)
(d)
Example 1:
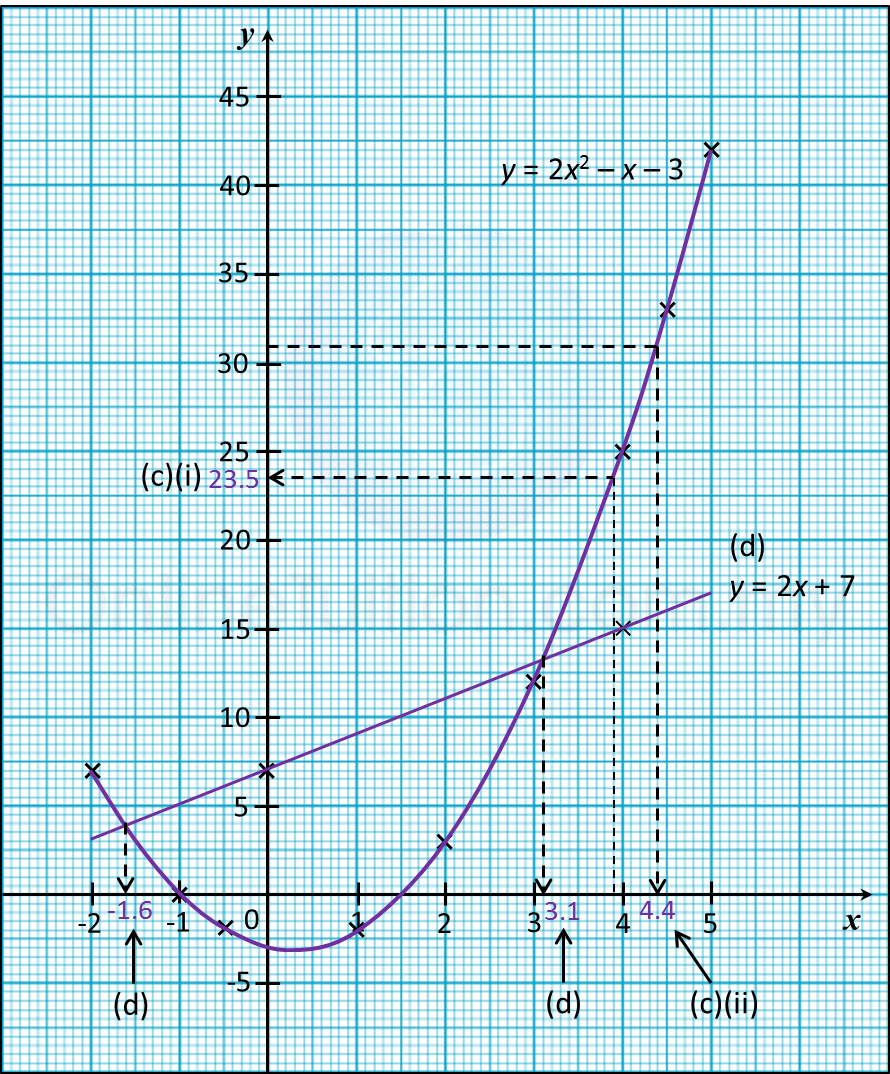
(a) The following table shows the corresponding values of x and y for the equation y = 2x2 – x – 3.
x |
–2 |
–1 |
–0.5 |
1 |
2 |
3 |
4 |
4.5 |
5 |
y |
7 |
m |
– 2 |
–2 |
3 |
12 |
n |
33 |
42 |
Calculate the value of m and n.
(b) For this part of the question, use graph paper. You may use a flexible curve rule.
By using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the y-axis, draw the graph of y = 2x2 – x – 3 for –2 ≤ x ≤ 5.
(c) From your graph, find
(i) The value of y when x = 3.9,
(ii) The value of x when y = 31.
(d) Draw a suitable straight line on your graph to find the values of x which satisfy the equation 2x2 – 3x = 10 for –2 ≤ x ≤ 5.
Solution:
(a)
y = 2x2 – x – 3
when x = –1,
m = 2 (–1)2 – (–1) – 3 = 0
when x = 4,
n = 2 (4)2 – (4) – 3 = 25
(b)

(c)
(i) From the graph, when x = 3.9, y = 23.5
(ii) From the graph, when y = 31, x = 4.4
(d)
y = 2x2 – x – 3 ----- (1)
2x2 – 3x = 10 ----- (2)
y = 2x2 – x – 3 ----- (1)
0 = 2x2– 3x – 10 ------ (2) ← (Rearrange (2))
(1) – (2) : y = 2x + 7
The suitable straight line is y = 2x + 7.
Determine the x-coordinates of the two points of intersection of the curve
y = 2x2 – x – 3 and the straight line y = 2x+ 7.
x |
0 |
4 |
y = 2x + 7 |
7 |
15 |
From the graph, x = –1.6, 3.1
2.1 Graphs of Functions (Part 2)
2.4 SPM Practice (Short Questions)
2.4.2 SPM Practice (Short Questions)
Question 3:
Which of the following graphs represent y = 2x3 – 16?


Solution:
y = 2x3 – 16
On the y-axis, x = 0.
y = 2(0)3 – 16
y = –16
The answer is C.
Question 4:
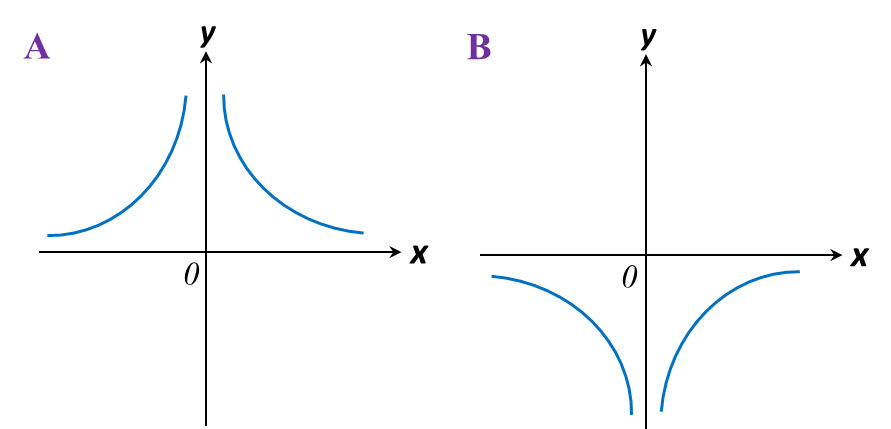
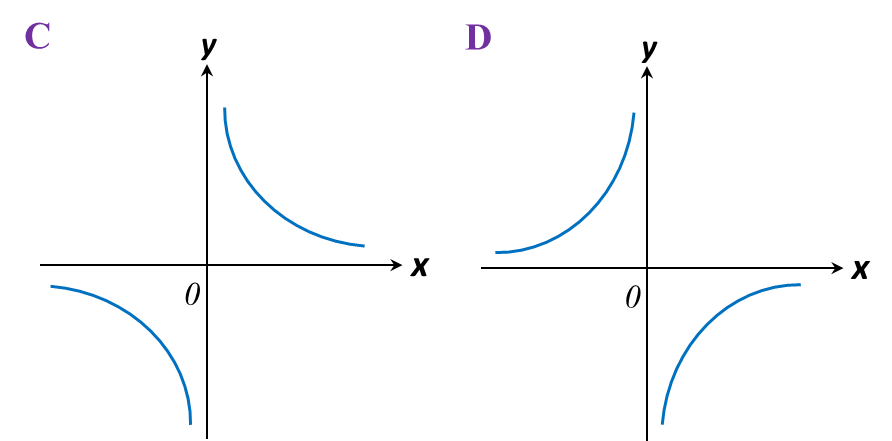
Which of the following graphs represent
y=−3x?
Solution:
y=−3x or y=−3x−1
Highest power of the variable x is –1.
It is a reciprocal function
y=ax, in this case a=−3.
The answer is D.
2.1 Graphs of Functions (Part 1)
2.1 Graphs of Functions
(A) Drawing graphs of functions
1. To draw the graph of a given function, the following steps are taken.
Step 1: Construct a table of values for the given function.
Step 2: Select a suitable scale for the x-axis and y-axis, if it is not given.
Step 3: Plot the points and complete the graph by joining the points.
Step 4: Label the graph.
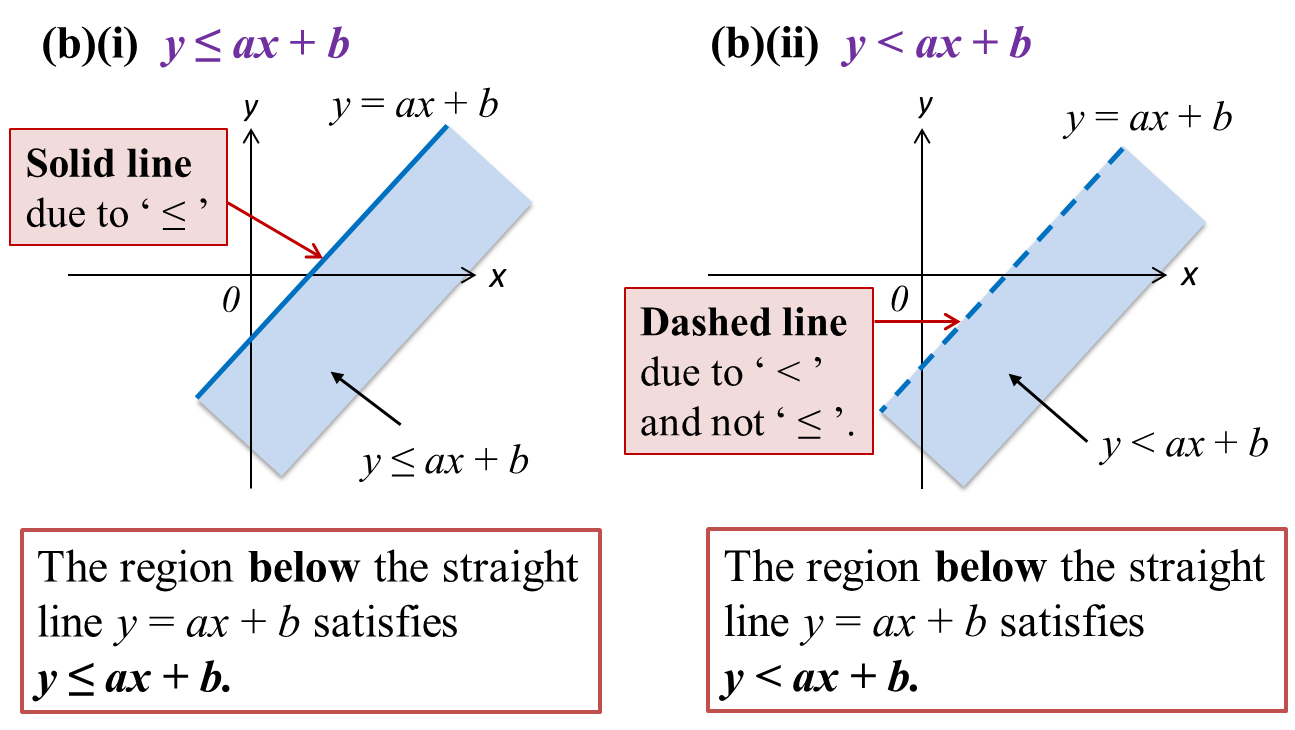
2.3 Region Representing inequalities in Two Variables (Part 1)
2.3.1 Position of a point relative to the graph of y = ax+ b
1. When y = ax + b, the point is on the line.
2. When y < ax + b, the point is below the line.
3. When y > ax + b, the point is above the line.
2.3.2 Identifying the region satisfying the respective inequalities.
1. A dashed line ‘----’ is used when points on the line are not included in the region representing the inequality, such as y > ax + b or y < a or x > a.
2. A solid line ‘___’ is used when points on the line are not included in the region representing the inequality, such as y ≥ ax + b or y ≤ a or x ≥ a.
3. The diagrams below show the regions that satisfy the respective inequalities.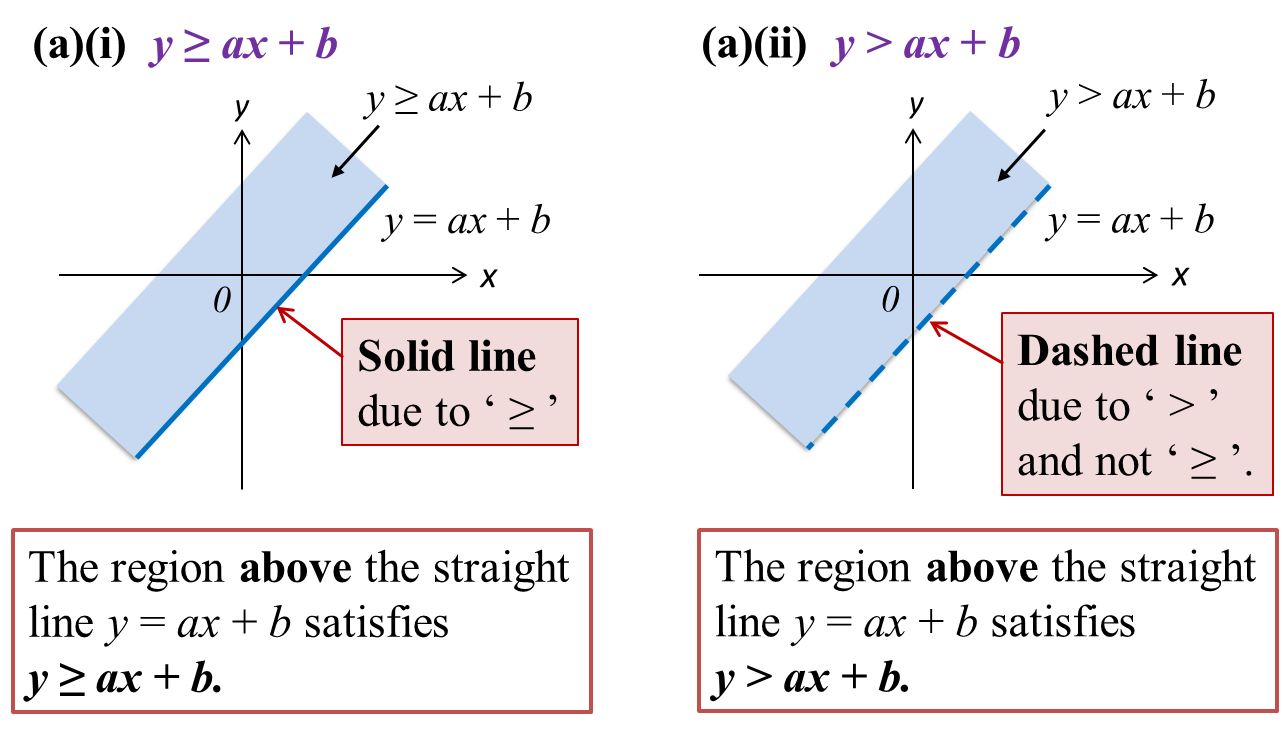
2.3.3 Region Representing inequalities in Two Variables (Sample Questions)
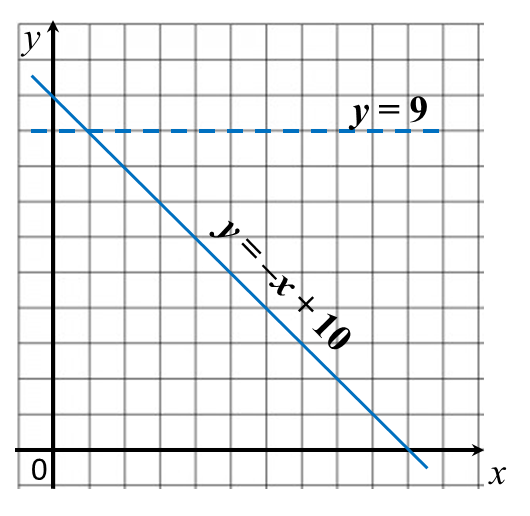
Example 1:
On the graph in the answer space, shade the region which satisfies the three inequalities y ≥ –x + 10, y > x and y < 9.
Answer:

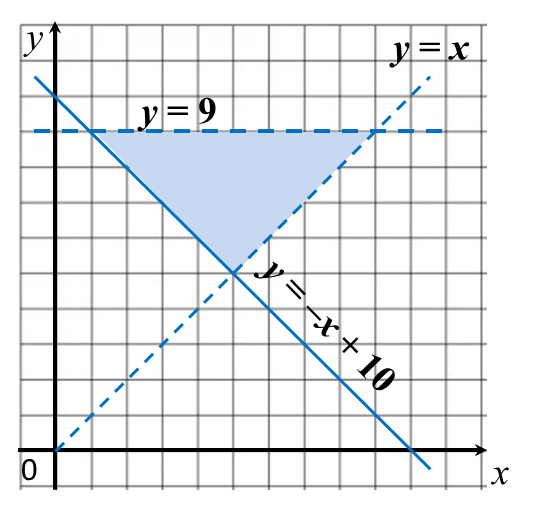
Solution:
1. The region that satisfies the inequality y ≥ –x + 10 is the region on and above the line y = –x + 10.
2. The region that satisfies the inequality y > x is the region above the line y = x. Since inequality sign “ >” is used, the points on the line y = x is not included. Thus, a dashed line needs to be drawn for y = x.
3. The region that satisfies the inequality y < 9 is the region below the line y = 9 drawn as a dashed line.

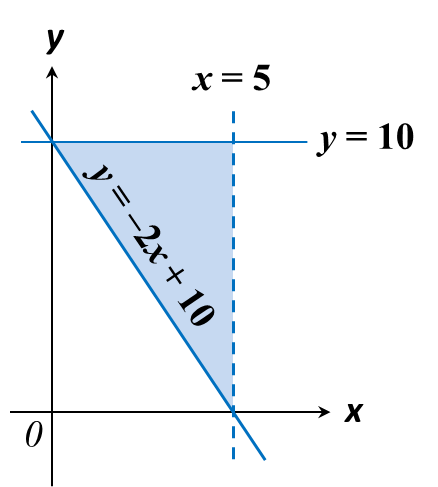
Example 2:
On the graph in the answer space, shade the region which satisfies the three inequalities y ≥ –2x + 10, y ≤ 10 and x < 5.
Answer:
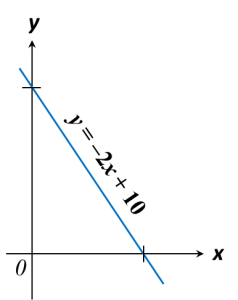

Solution:
1. The region which satisfies the inequality of the form y ≥ ax + c is the region that lies on and above the line y = ax+ c.
2. In this question, y intercept, c = 10, x intercept is 5.
3. The region that satisfies the inequality y ≥ –2x + 10 is the region on and above the line y = –2x + 10.
4. The region that satisfies the inequality y ≤ 10 is the region on and below the line y = 10.
5. The region that satisfies the inequality x < 5 is on the left of the line x = 5 drawn as a dashed line.