Question 13 (5 marks):
(a) State whether the following statements are true statement or false statement.
(i) { }⊂{ S,E,T }(ii) { 1 }⊂{ 1,2,3 }={ 1,2,3 }
(b) Diagram 7 shows the first three patterns of a sequence of patterns.
 Diagram 7
Diagram 7
It is given that the diameter of each circle is 20 cm.
(i) Make a general conclusion by induction for the area of the unshaded region.
(ii) Hence, calculate the area of the unshaded region for the 5th pattern.
Solution:
(a)(i) True
(a)(ii) False
(b)(i)
Area of unshaded region (first)
= (20 × 20) – π(10)2
= 400 – 100π
= 100 (4 – π)
Area of unshaded region (second)
= 4 × 100 (4 – π)
= 400 (4 – π)
Area of unshaded region (third)
= 9 × 100 (4 – π)
= 900 (4 – π)
100 (4 – π), 400 (4 – π), 900 (4 – π), …
102 (4 – π), 202 (4 – π), 302 (4 – π), …
General conclusion = n2 (4 – π)
n = 10, 20, 30, …
(b)(ii)
Area of unshaded region (5th)
= 502 (4 – π)
= 2500 (4 – π)
(a) State whether the following statements are true statement or false statement.
(i) { }⊂{ S,E,T }(ii) { 1 }⊂{ 1,2,3 }={ 1,2,3 }
(b) Diagram 7 shows the first three patterns of a sequence of patterns.
 Diagram 7
Diagram 7It is given that the diameter of each circle is 20 cm.
(i) Make a general conclusion by induction for the area of the unshaded region.
(ii) Hence, calculate the area of the unshaded region for the 5th pattern.
Solution:
(a)(i) True
(a)(ii) False
(b)(i)
Area of unshaded region (first)
= (20 × 20) – π(10)2
= 400 – 100π
= 100 (4 – π)
Area of unshaded region (second)
= 4 × 100 (4 – π)
= 400 (4 – π)
Area of unshaded region (third)
= 9 × 100 (4 – π)
= 900 (4 – π)
100 (4 – π), 400 (4 – π), 900 (4 – π), …
102 (4 – π), 202 (4 – π), 302 (4 – π), …
General conclusion = n2 (4 – π)
n = 10, 20, 30, …
(b)(ii)
Area of unshaded region (5th)
= 502 (4 – π)
= 2500 (4 – π)
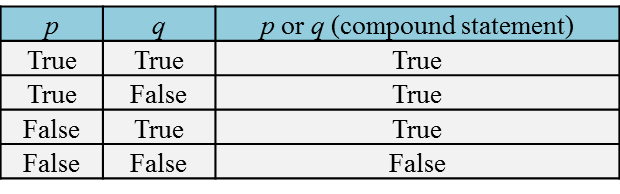
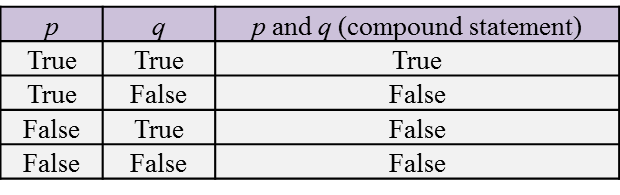
 Table 1
Table 1