Answer:
4.1 Statements (Sample Questions)
Answer:
Maths Tip
1. General statement → Special conclusion → Deduction
2. Specific cases → General conclusion → Induction
|
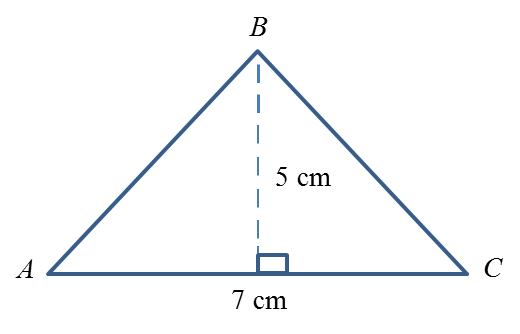 Area of ∆ ABC
Area of ∆ ABC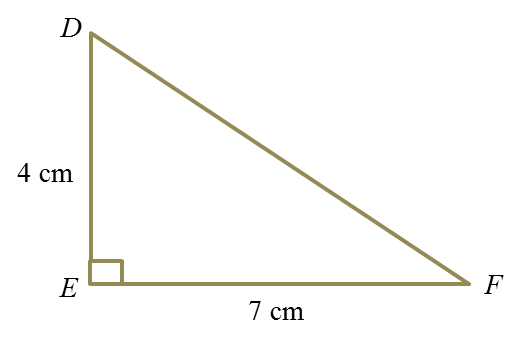
Identify the antecedent and consequent of the following implications.
(a) If m = 2, then 2m2 + m = 10
Given that p: x + 1 = 8
q: x = 7
Construct a mathematical statement in the form of implication
Write down two implications based on the following sentence:
x3 = 64 if and only if x = 4.
If x3 = 64, then x = 4.
If x = 4, then x3 = 64.
State the converse of each of the following implications.
| 3 + 3 = 9 or 3 × 3 = 9 |
| If x > 3, then x > 7 |
| x + 7 = 9 |
Identify the premises and conclusion of the following argument.
Premise 1: A pentagon has 5 sides.
Premise 2: ABCDE is a pentagon.
Conclusion: ABCDE has 5 sides.
|
Premise 1: All A are B. Premise 2: C is A. Conclusion: C is B. |
Make a conclusion based on the two premises given below.
Premise 1: All multiples of 5 are divisible by 5.
Premise 2: 45 is a multiple of 5.
Conclusion: _______________
Conclusion: 45 is divisible by 5.
|
Premise 1: If p, then q. Premise 2: p is true. Conclusion: q is true. |
Make a conclusion based on the two premises given below.
Premise 1: If a number is a factor of 18, then the number is a factor of 54.
Premise 2: 3 is a factor of 18.
Conclusion: _______________
Conclusion: 3 is a factor of 54.
|
Premise 1: If p, then q. Premise 2: Not q is true. Conclusion: Not p is true. |
Make a conclusion based on the two premises given below.
Premise 1: If P is a subset of Q, then P ∩ Q = P .
Premise 2: P ∩ Q ≠ P
Conclusion: _______________
Conclusion: P is not the subset of Q.
A ∩ B = B if and only if A υ B = A. |
Premise 1: If a number is a factor of 24, then it is a factor of 48.
Premise 2: 12 is a factor of 24.
Conclusion: _____________________
|
Premise 1: _____________________
Premise 2: x is a multiple of 25.
Conclusion: x is a divisible of 5. |
Premise 1: All A are B.
Premise 2: C is A.
Conclusion: C is B. |
Premise 1: If p, then q.
Premise 2: p is true.
Conclusion: q is true. |
Premise 1: If p, then q.
Premise 2: Not q is true.
Conclusion: Not p is true. |