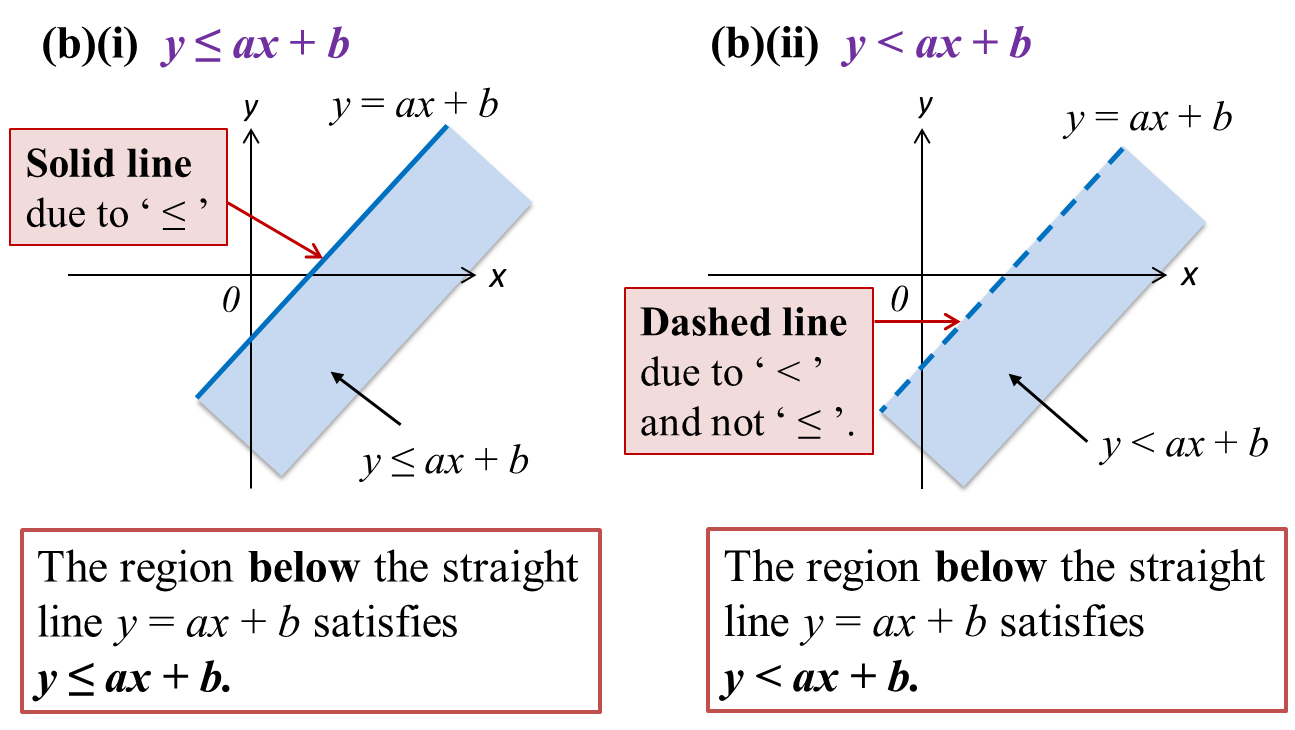
2.3.1 Position of a point relative to the graph of y = ax+ b
1. When y = ax + b, the point is on the line.
2. When y < ax + b, the point is below the line.
3. When y > ax + b, the point is above the line.
2.3.2 Identifying the region satisfying the respective inequalities.
1. A dashed line ‘----’ is used when points on the line are not included in the region representing the inequality, such as y > ax + b or y < a or x > a.
2. A solid line ‘___’ is used when points on the line are not included in the region representing the inequality, such as y ≥ ax + b or y ≤ a or x ≥ a.
3. The diagrams below show the regions that satisfy the respective inequalities.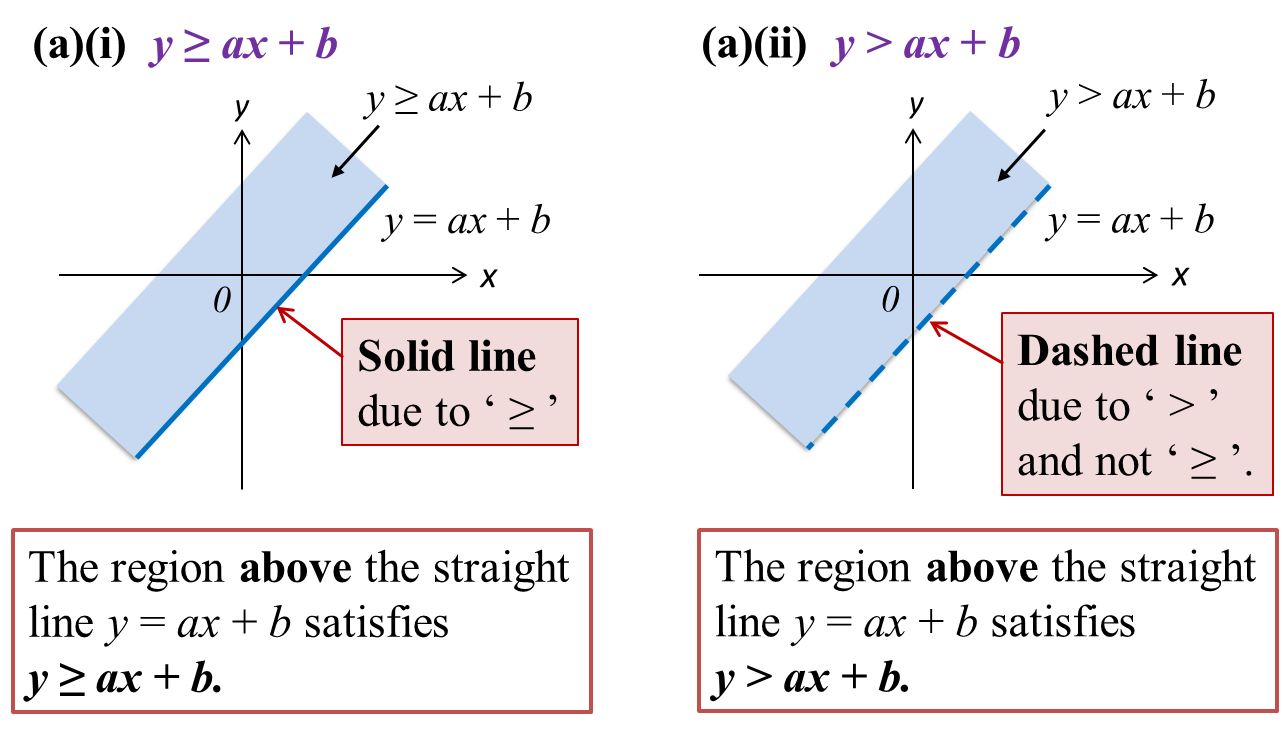
2.3.3 Region Representing inequalities in Two Variables (Sample Questions)
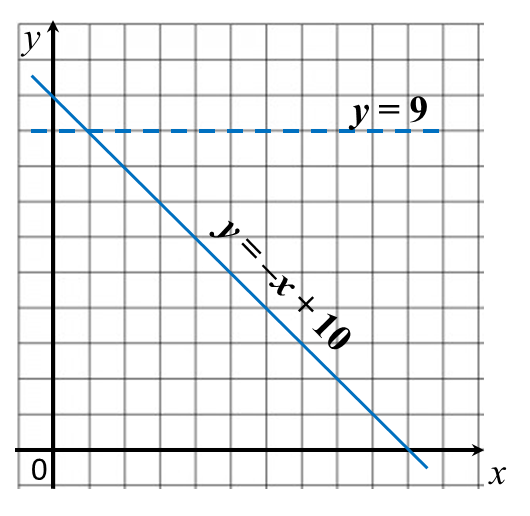
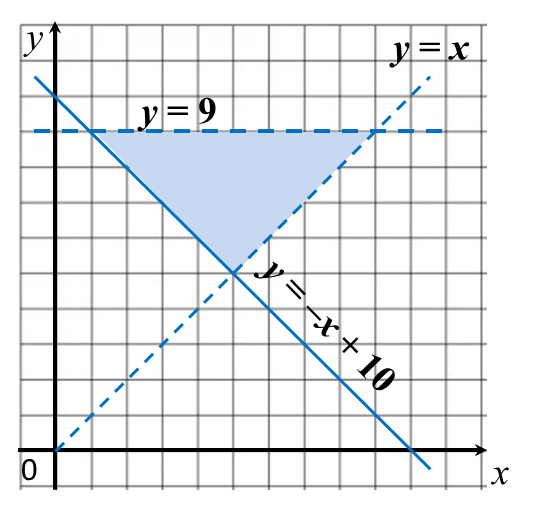
Example 1:
On the graph in the answer space, shade the region which satisfies the three inequalities y ≥ –x + 10, y > x and y < 9.
Answer:

Solution:
1. The region that satisfies the inequality y ≥ –x + 10 is the region on and above the line y = –x + 10.
2. The region that satisfies the inequality y > x is the region above the line y = x. Since inequality sign “ >” is used, the points on the line y = x is not included. Thus, a dashed line needs to be drawn for y = x.
3. The region that satisfies the inequality y < 9 is the region below the line y = 9 drawn as a dashed line.

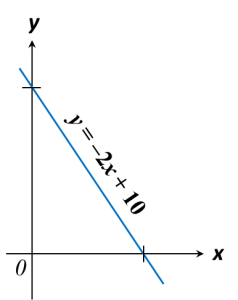
Example 2:
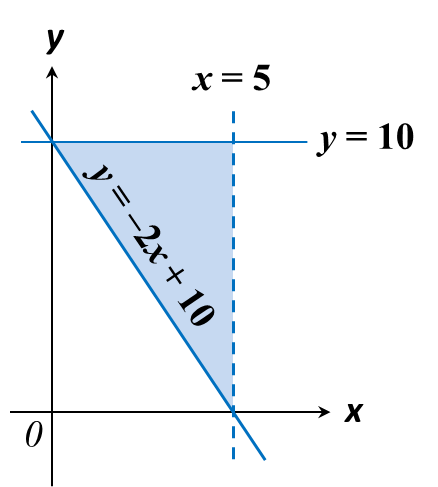
On the graph in the answer space, shade the region which satisfies the three inequalities y ≥ –2x + 10, y ≤ 10 and x < 5.
Answer:

Solution:
1. The region which satisfies the inequality of the form y ≥ ax + c is the region that lies on and above the line y = ax+ c.
2. In this question, y intercept, c = 10, x intercept is 5.
3. The region that satisfies the inequality y ≥ –2x + 10 is the region on and above the line y = –2x + 10.
4. The region that satisfies the inequality y ≤ 10 is the region on and below the line y = 10.
5. The region that satisfies the inequality x < 5 is on the left of the line x = 5 drawn as a dashed line.

1.2 SPM Practice (Short Questions)
Question 2:
Solution:
State the value of the digit 6 in the number 16238, in base ten.
Solution:
Identify the place value of each digit in the number first.
1 |
6 |
2 |
3 |
|
Place Value |
83 |
82 |
81 |
80 |
Value of the digit 6
= 6 × 82
= 384
Question 3:
Solution:
Given 3 × 53 + 4 × 52 + 5p = 34205, find the value of p.
34205 = 3 × 53 + 4 × 52+ 2 × 51 + 0 × 50
34205 = 3 × 53 + 4 × 52+ 5p+ 0
5p = 2 × 51
5p = 10
p = 2
Question 4:
Solution:
Convert 4 × 84 + 2 × 82 + 4 to a number in base eight.
84 |
83 |
82 |
81 |
80 |
4 |
0 |
2 |
0 |
48 |
Answer = 402048
1.1 Number Bases (Part 1)
(A) Numbers in Bases Two, Eight and Five
1. The numbers we use daily are in base ten. The ten digits used in numbers in based ten are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
2. Numbers in base two are numbers that use two digits only. The digits are 0 and 1. Example: 1011012.
3. Numbers in base eight are numbers that use eight digits only. The eight digits used in numbers in based ten are 0, 1, 2, 3, 4, 5, 6, and 7.
Example: 6758.
4. Numbers in base five are numbers that use five digits only. The five digits used in numbers in based five are 0, 1, 2, 3, and 4. Example: 1345.
(B) Value of a Digit of a Number in Base 2, 8 and 5
1. The following tables show the place values of the digits of a number
(a) In base 2
Place value |
26 = 64 |
25 = 32 |
24 = 16 |
23 = 8 |
22 = 4 |
21 = 2 |
20 = 1 |
(b) In base 8
Place value |
84 = 4096 |
83 = 512 |
82 = 64 |
81 = 8 |
80 = 1 |
(c) In base 5
Place value |
54 = 625 |
53 = 125 |
52 = 25 |
51 = 5 |
50 = 1 |
2.
|
Value of a digit = The digit × Place value of the digit
|
Example 1:
State the value of the underlined digit in each of the following numbers.
(a) 10111012 (b) 36518 (c) 32415
Solution:
(a)
= 1 × 26The value of the underlined digit 1
Place value |
26 = 64 |
25 = 32 |
24 = 16 |
23 = 8 |
22 = 4 |
21 = 2 |
20 = 1 |
Number |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
= 1 × 64
= 64
(b)
Place value |
83 = 512 |
82 = 64 |
81 = 8 |
80 = 1 |
Number |
3 |
6 |
5 |
1 |
= 6 × 82
The value of the underlined digit 6
The value of the underlined digit 6
= 6 × 64
= 384
(c)
Place value |
53 = 125 |
52 = 25 |
51 = 5 |
50 = 1 |
Number |
3 |
2 |
4 |
1 |
The value of the underlined digit 3
= 3 × 125
= 375
(C) Writing a Number in Base 2, 8, or 5 in Expanded Notation
1. A number written in expanded notation refers to the sum of the value of the digits that make up the number.
Example 2:
Write each of the following in expanded notation.
(a) 1110112 (b) 4758 (c) 24135
Solution:
(a)
Place value |
25 = 32 |
24 = 16 |
23 = 8 |
22 = 4 |
21 = 2 |
20 = 1 |
Number |
1 |
1 |
1 |
0 |
1 |
1 |
(b)
Place value |
82 = 64 |
81 = 8 |
80 = 1 |
Number |
4 |
7 |
5 |
(c)
Place value |
53 = 125 |
52 = 25 |
51 = 5 |
50 = 1 |
Number |
2 |
4 |
1 |
3 |
1.1 Number Bases (Part 2)
(D) Converting Numbers in Base Two, Eight and Five to Base Ten and Vice Versa
1. Steps to convert numbers in base 2, 8 and 5 to base 10 are as follows.
(a) write the number in expanded notation.
(b) simplify the expanded notation into a single number.
Example 1:
Convert each of the following numbers to a number in base 10.
(a) 101012 (b) 14238 (c) 3245
Solution:
(a) 101012 = 1 × 24 + 0 × 23+ 1 × 22 + 0 × 21 + 1 × 20 = 2110
(b) 14238 = 1 × 83 + 4 × 82+ 2 × 81 + 3 × 80 = 78710
(c) 3245 = 3 × 52 + 2 × 51+ 4 × 50 = 8910
Calculator Computation
1. Set the calculator to the ‘BASE’ mode by pressing:
[MODE] [MODE] [3 (BASE)]
2. Set the calculator to the desired number system by pressing:
[BIN] → for base 2
[DEC] → for base 10
[OCT] → for base 8
Key in the following:
(a)
[BIN] 10101 [=] [ DEC ]
The screen display is: [21]
Therefore 101012 = 2110
(b)
[OCT] 1423 [=] [ DEC ]
The screen display is: [787]
Therefore 14238 = 78710
|
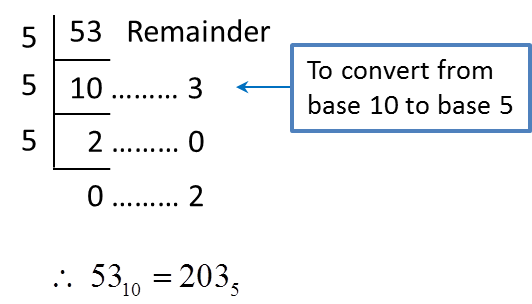
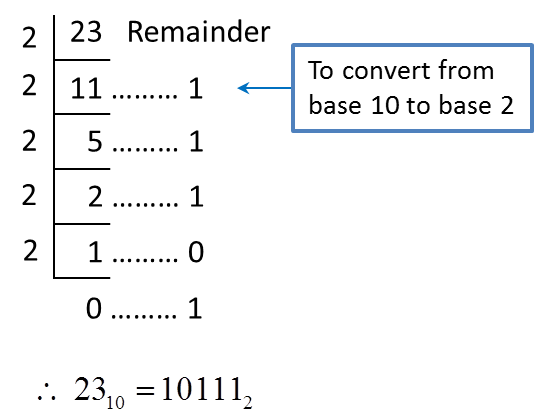
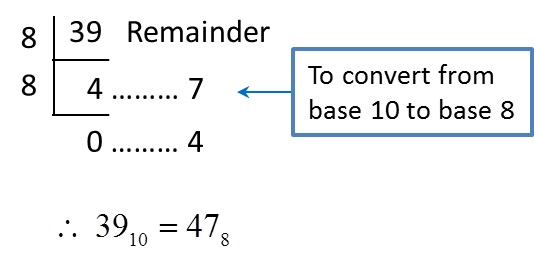
2. Steps to convert a number in base 10 to a number in base 2, 8 and 5 are as follows.
(a) perform repeated division until the quotient is zero.
(b) write the number in new base by referring to the remainders from bottom to the top.
Example 2:
Convert 6110 to a number in
(a) Base two (b) base eight (c) base five
Solution:
(a)
(b)
(c)
Calculator Computation
1. Set the calculator to the ‘BASE’ mode by pressing:
[MODE] [MODE] [3 (BASE)]
2. Set the calculator to the desired number system by pressing:
[BIN] → for base 2
[DEC] → for base 10
[OCT] → for base 8
Key in the following:
(a)
[DEC] 61 [=] [ BIN ]
The screen display is: [1111012]
Therefore 6110 = 1111012
(b)
[DEC] 61 [=] [ OCT ]
The screen display is: [75]
Therefore 6110 = 758
|
1.1 Number Bases (Part 4)
(F) Addition and Subtraction of Two Numbers in Base Two
1. In the addition of two numbers in base two, the following rules applied:
|
02 + 02 = 02
02 + 12 = 12
12 + 02 = 12
12 + 12 = 102
12 + 12 + 12 = 102 + 12 = 112
|
2. In the subtraction of two numbers in base two, the following rules applied:
|
02 – 02 = 02
12 – 02 = 12
12 – 12 = 02
102 – 12 = 12
|
Example 2:
Find the value of each of the following:
(a) 11012 + 1102
(b) 110012 + 101002
(c) 110112 – 11012
(d) 10002 – 1012
Solution:
(a)(b)
(c)
(d)
Calculator Computation
You may obtain the answer directly from a scientific calculator by pressing:
[MODE] [MODE] [3 (BASE)]
Key in the following:
(a)
[ BIN ] 1101 [ + ] 110 [ = ]
The screen display is: [ 10011 ]
(b)
[ BIN ] 11001 [ + ] 11100 [ = ]
The screen display is: [ 110101 ]
(c)
[ BIN ] 11011 [ – ] 1101 [ = ]
The screen display is: [ 1110 ]
(d)
[ BIN ] 1000 [ – ] 101 [ = ]
The screen display is: [ 11 ]
|
1.1 Number Bases (Part 3)
(E) Converting from One Base to Another
1. The following steps are used to convert a number from one base to another base.
(a) convert the number to a number in base 10 by using expended notation.
(b) use repeated division to convert the number in base 10 to the respective bases.
Example 1:
Convert
(a) 1101012 to a number in base 5
(b) 435 to a number in base 2
(c) 3138 to a number in base 5
(d) 4225 to a number in base 8
(e) 1001112 to a number in base 8
(f) 1578 to a number in base 2
(f) 1578 to a number in base 2
Solution:
(a) 1101012
= 1 × 25 + 1 × 24 + 0 × 23+ 1 × 22 + 0 × 21 + 1 × 20
= 5310 ← (Convert from base 2 to base 10)
(b) 435
= 4 × 51 + 3 × 50
= 2310← (Convert from base 5 to base 10)
(c) 3138
= 3 × 82 + 1 × 81 + 3 × 80
= 20310← (Convert from base 8 to base 10)
(d) 4225
= 4 × 52 + 2 × 51 + 2 × 50
= 11210← (Convert from base 5 to base 10)
(e) 1001112
= 1 × 25 + 0 × 24 + 0 × 23+ 1 × 22 + 1 × 21 + 1 × 20
= 3910 ← (Convert from base 2 to base 10)

(f) 1578
= 1 × 82 + 5 × 81 + 7 × 80
= 11110← (Convert from base 8 to base 10)

Calculator Computation
1. Set the calculator to the ‘BASE’ mode by pressing:
[MODE] [MODE] [3 (BASE)]
2. Set the calculator to the desired number system by pressing:
[BIN] → for base 2
[DEC] → for base 10
[OCT] → for base 8
Key in the following [For (e) and (f) only]:
(e)
[ BIN ] 100111 [ = ] [ OCT ]
The screen display is: [478]
Therefore 1001112 = 478
(f)
[ OCT ] 157 [ = ] [ BIN ]
The screen display is: [1101111]
Therefore 1578 = 11011112
|
10.2 Solving Problems Involving Angle of Elevation and Angle of Depression
Example:


The angle of depression of a cycling kid measured from a hill with 10.9 m high is 52o. When the kid cycles along the hillside and stops, the angle of depression becomes 25.3o. What is the distance cycled by the kid along the hillside?
Solution:


Step 1: Draw a diagram to represent the situation.
Step 2: Devise a plan.
Find the lengths of QS and QR. Then, QS – QR = distance cycled by the kid.


QS – QR = (23.1 – 8.5) m = 14.6 m
Therefore the kid has cycled 14.6 metres.
SPM Practice (Short Questions)
Question 1:
Diagram below shows two vertical poles on a horizontal plane. J, K, L, M and N are five points on the poles such that KL = MN.
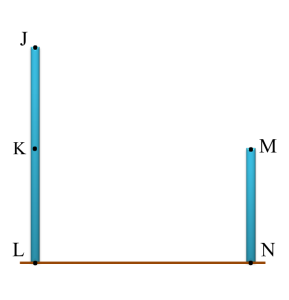

Name the angle of elevation of point J from point M.
Solution:
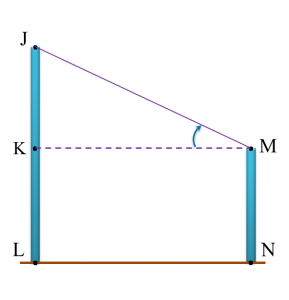
Angle of elevation of point J from point M = ∠KMJ
Question 2:
Diagram below shows two vertical poles JM and KL, on a horizontal plane.
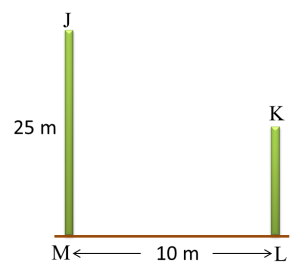

The angle of depression of vertex K from vertex J is 42o.
Calculate the angle of elevation of vertex K from M.
Solution:
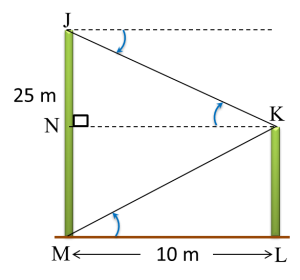
JN = 10 tan 42o = 9.004 m
NM = 25 – 9.004 = 15.996 m
KL = NM = 15.996 m
Question 3:
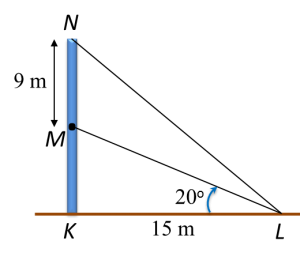
Diagram below shows a vertical pole KMN on a horizontal plane. The angle of elevation of M from L is 20o.
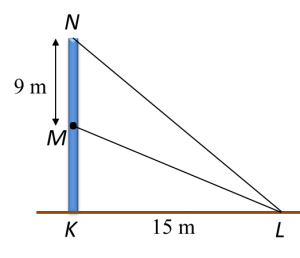
Calculate the height, in m, of the pole.
Solution:
10.1 Angle of Elevation and Angle of Depression (Part 1)
10.1 Angle of Elevation and Angle of Depression (Part 1)
1. Angle of elevation is the acute angle measured from a horizontal line up to the line of sight.


Example 1:


Angle of elevation of object O from P = ∠OPA
2. Angle of depression is the acute angle measured down from a horizontal line to the line of sight.


Example 2:


Angle of depression of object O from P = ∠OPA