SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

Diagram below shows three vertical poles JP, KN and LM, on a horizontal plane.

The angle of elevation of N from P is 15^o.

The angle of depression of M from N is 35^o.

Calculate the distance, in m, from K to L.

Solution:

\begin{array}{l} \tan ∠ A P N = \frac{A N}{P A} \\ \tan 15^{o} = \frac{A N}{4} \\ A N = 4 \times 0.268 \\ A N = 1.072 m \\ Length of B N = 2 + 1.072 = 3.072 c m \\ \tan ∠ B M N = \frac{B N}{B M} \\ \tan 35^{o} = \frac{3.072}{B M} \\ B M = \frac{3.072}{0.700} = 4.389 \\ Distance of K L = 4.389 m \end{array}

Question 5:

Diagram below shows two vertical poles JM and LN, on a horizontal plane.

The angle of elevation of M from K is 70^oand the angle of depression of K from N is 40^o.

Find the difference in distance, in m, between JK and KL.

Solution:

\begin{array}{l} \tan ∠ J K M = \frac{14}{J K} \\ J K = \frac{14}{\tan 70^{o}} \\ J K = 5.096 m \\ \tan ∠ L K N = \frac{8}{K L} \\ K L = \frac{8}{\tan 40^{o}} \\ K L = 9.534 m \\ Difference in distance of J K and K L \\ = 9.534 - 5.096 \\ = 4.438 m \end{array}

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 7:

Which graph represents y = sin x for 0^o ≤ x ≤ 270^o?

Solution:

Answer: B

Question 8:

Which graph represents y = sin x for 0^o ≤ x ≤ 180^o?

Solution:

Answer: D

Question 9:

Which graph represents part of y = sin x?

Solution:

Answer: A

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 10:

Which of the following graph represents y = cos 2x?

Solution:

Answer: C

Question 11:

Which of the following graph represents y = cos x for 0^o ≤ x ≤ 180^o?

Solution:

Answer: D

Question 12:

Which graph represents part of y = cos x?

Solution:

Answer: B

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 13:

Which of the following graph represents y = tan x for 0^o ≤ x ≤ 360^o?

Solution:

Answer: A

Question 14:

Which graph represents part of y = tan x?

Solution:

Answer: C

9.2 Graphs of Sine, Cosine and Tangent

Posted on April 23, 2020 by user

9.2 Graphs of Sine, Cosine and Tangent

(1) y = sin x, 0^o≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
*sin x*	0	1	0	-1	0

(2) y = cos x, 0^o≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
*cos x*	1	0	-1	0	1

(3) y = tan x, 0^o≤ x ≤ 360^o

x	0^o	90^o	180^o	270^o	360^o
*tan* x	0	∞	0	∞	0

(4) y = sin 2x, 0^o≤ 2x ≤ 360^o
(5) y = cos 2x, 0^o≤ 2x ≤ 360^o

(6) y = tan 2x, 0^o≤ 2x ≤ 360^o

9.1 Values of Sine, Cosine and Tangent of an Angle (Part 1)

Posted on April 23, 2020 by user

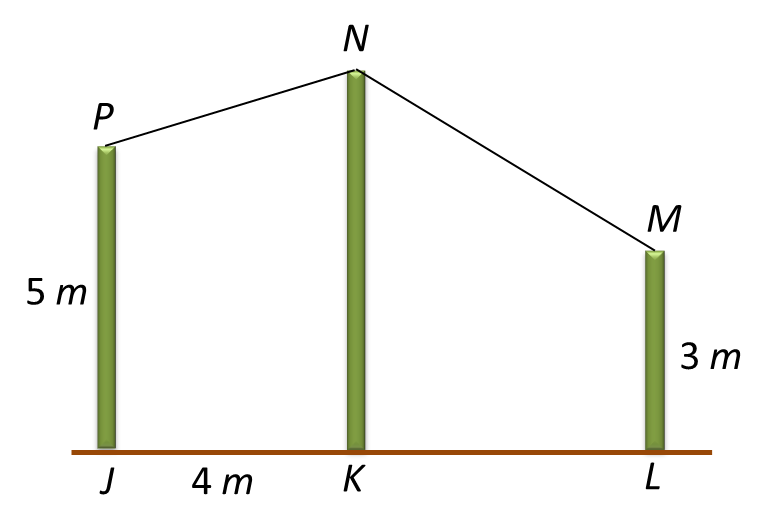
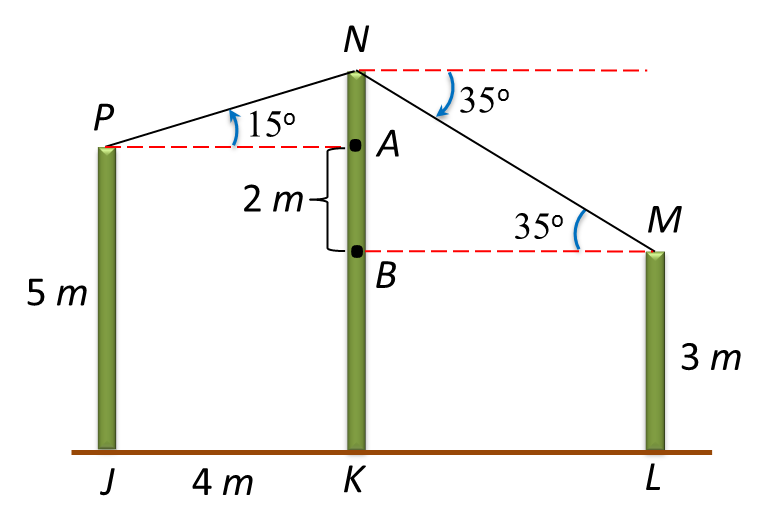
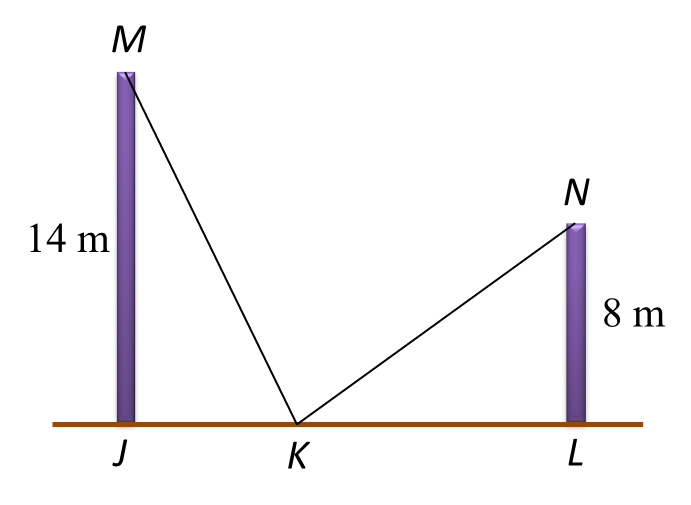
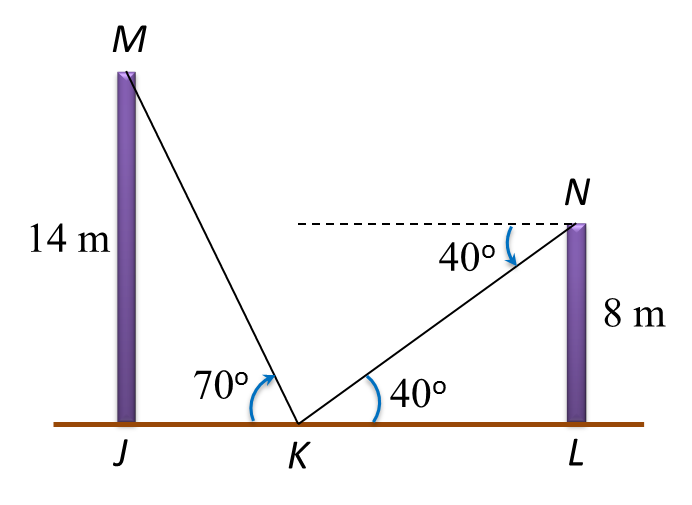
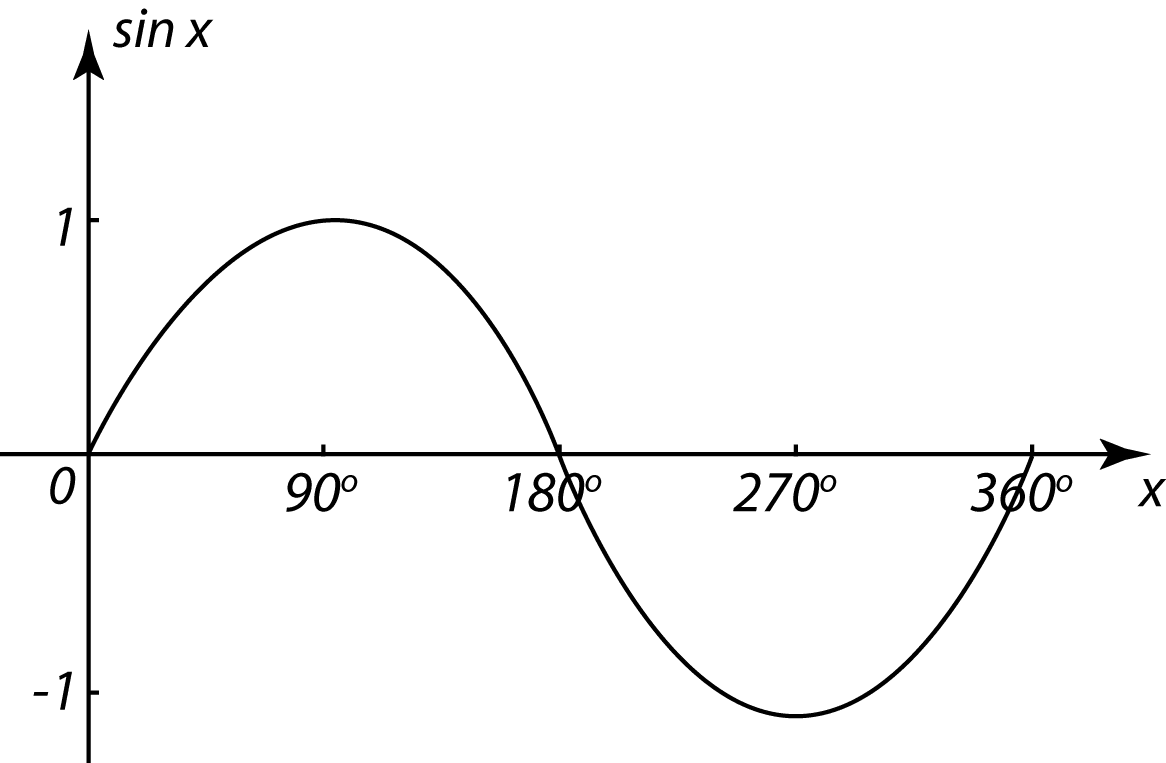
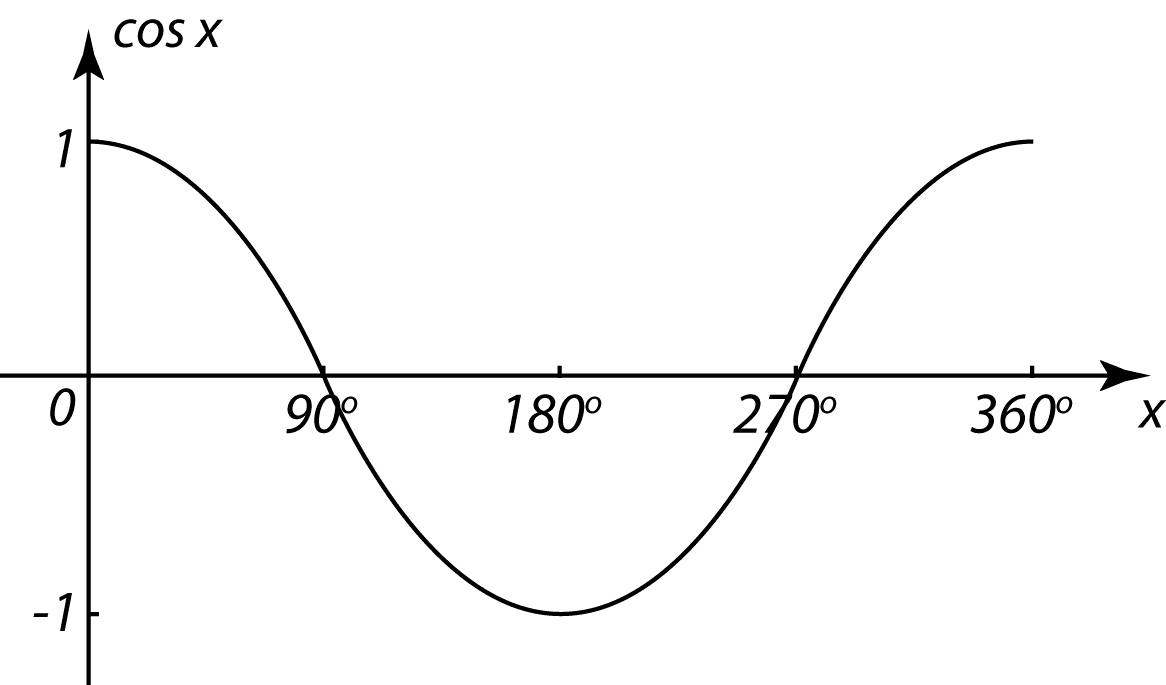
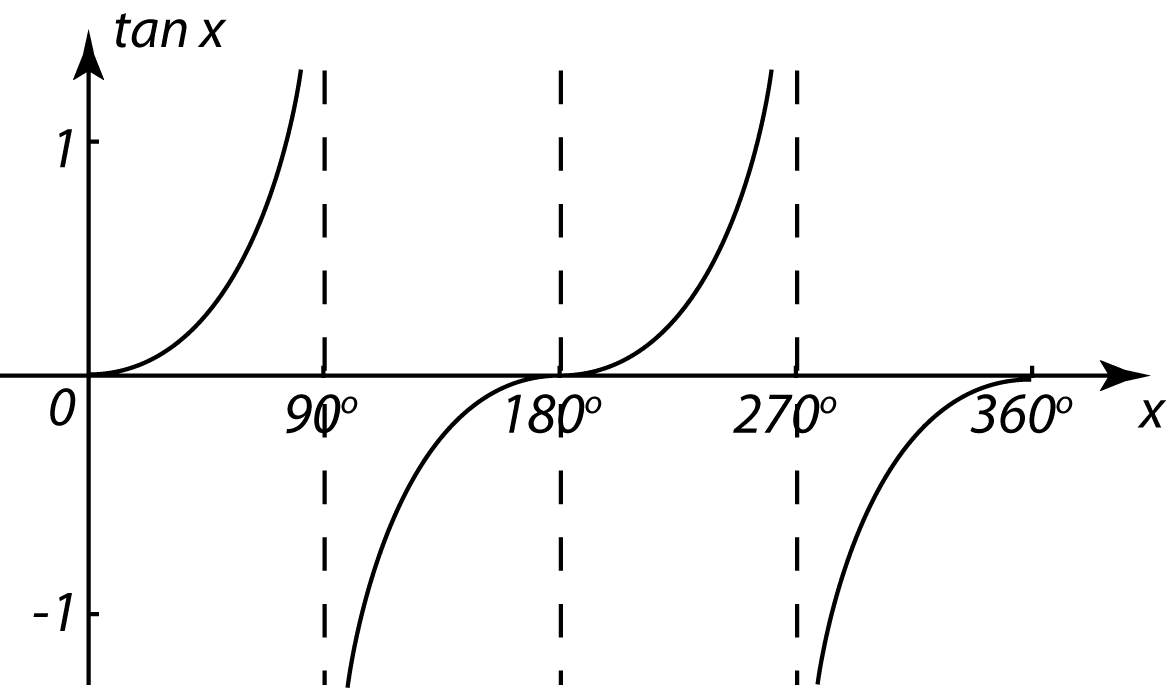9.1 Values of Sine, Cosine and Tangent of an Angle

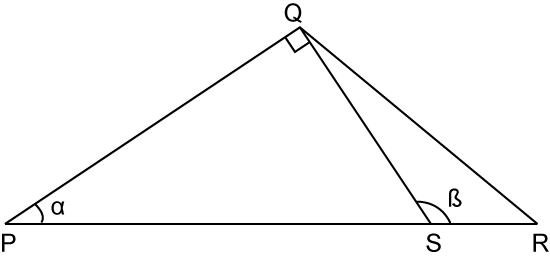
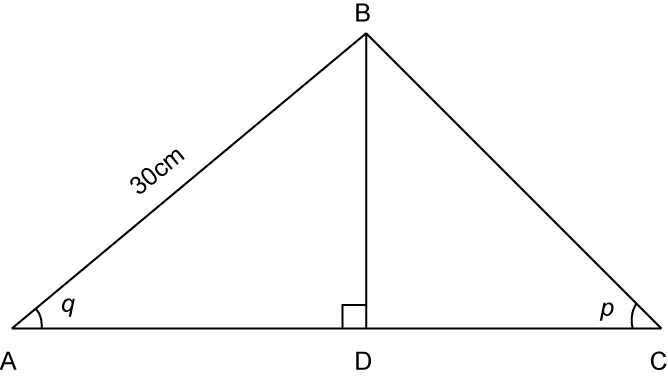
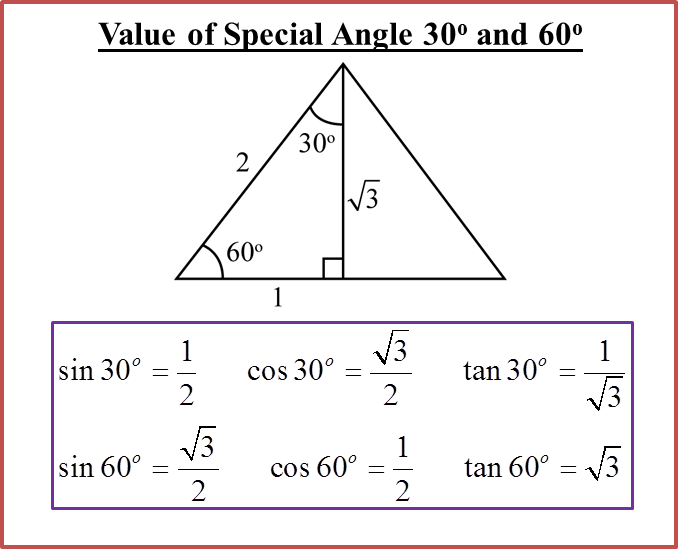
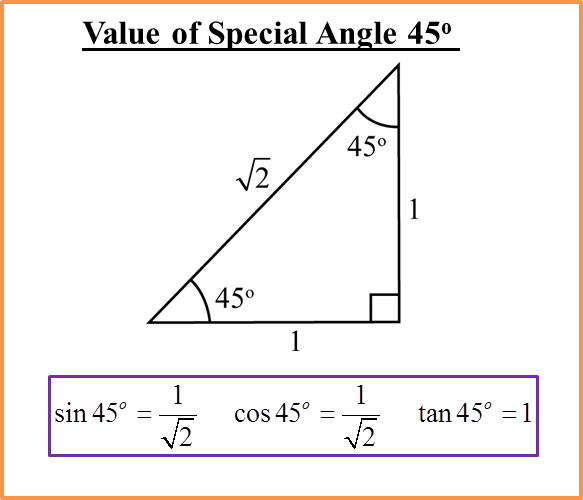
(A) Sine, Cosine and Tangent for Right-Angled Triangles

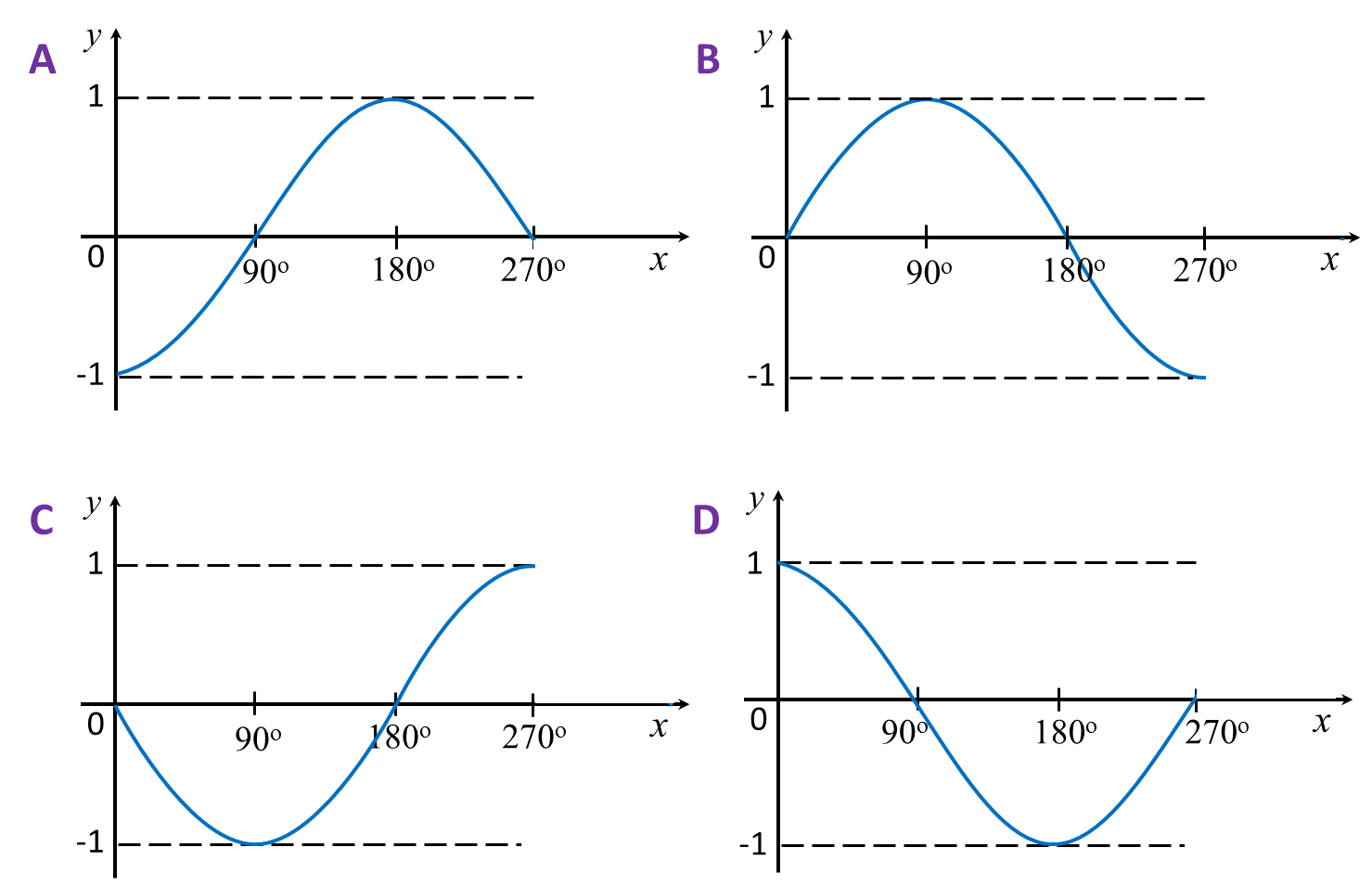
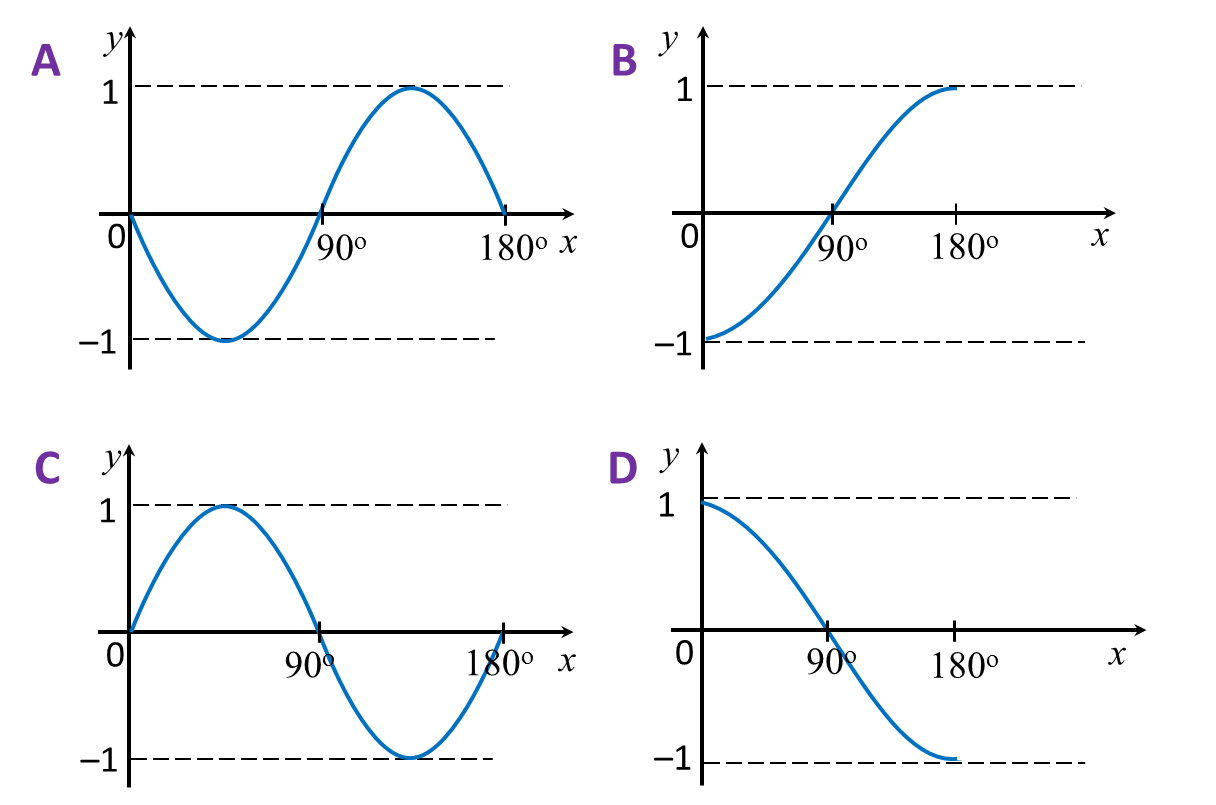
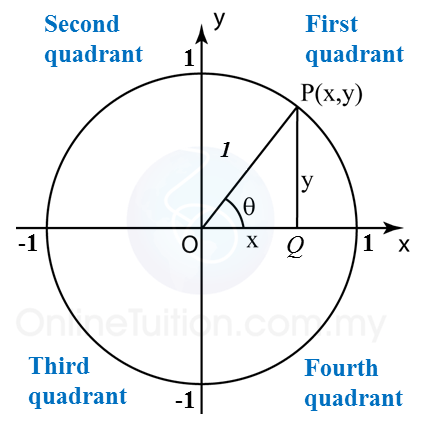
\begin{array}{l} \sin θ = \frac{opposites side}{hypotenuse} \\ cos θ = \frac{adjacent side}{hypotenuse} \\ tan θ = \frac{opposites side}{adjacent side} \end{array}

(B) Values of Sin θ, Cos θ and Tan θ in First Quadrant of the Unit Circle

In first quadrant, P is a point on the circumference of the unit circle with centre O, θ is the angle between the radius OP and the positive x-axis. From the diagram,

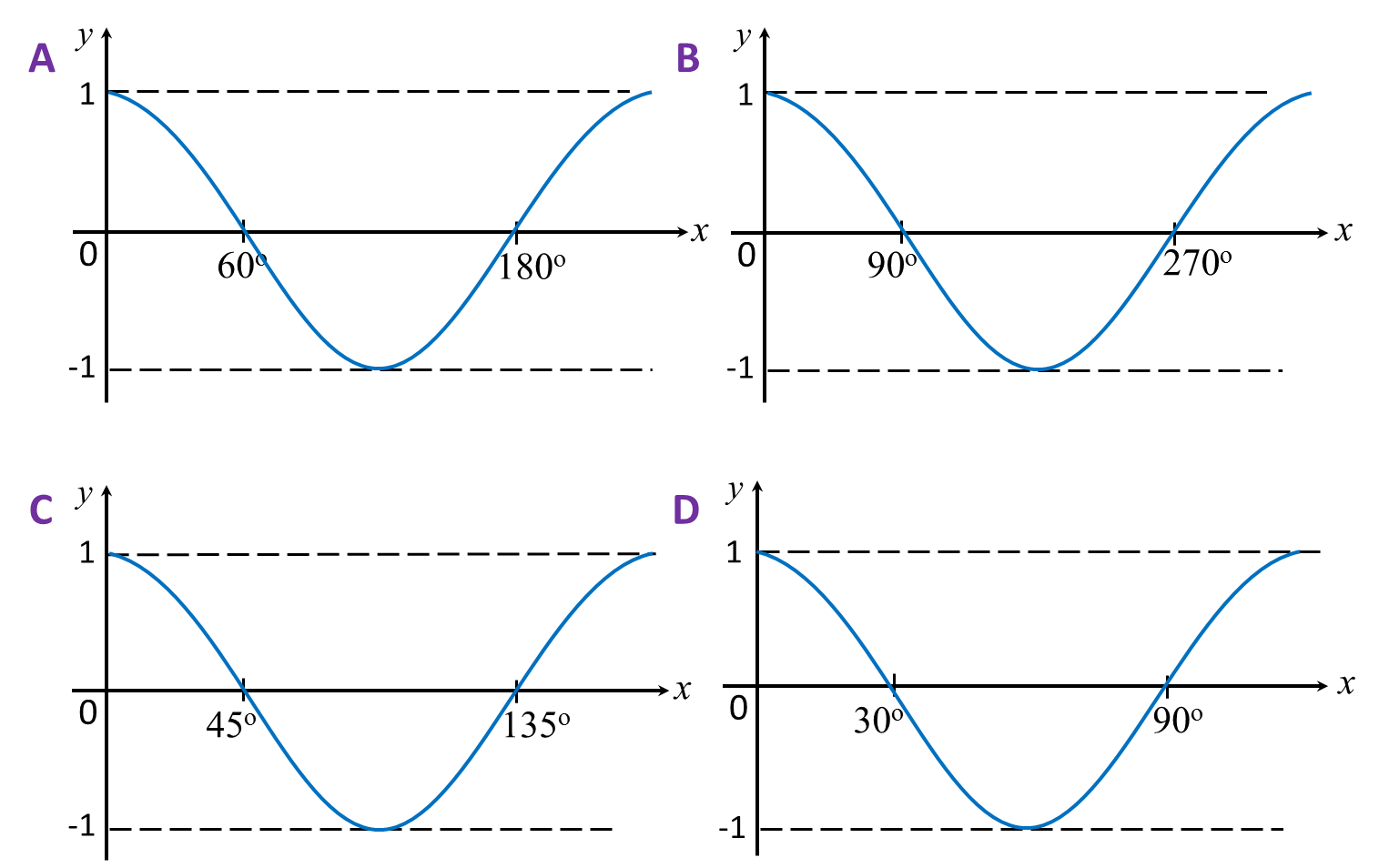
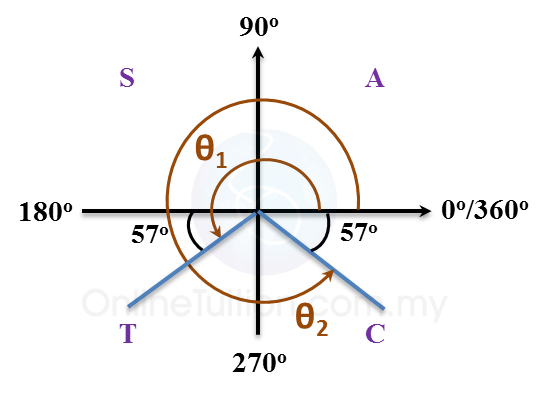
\begin{array}{l} (a) sin θ = \frac{P Q}{O P} = y \\ (b) cos θ = \frac{O Q}{O P} = x \\ (c) tan θ = \frac{P Q}{O Q} = \frac{y}{x} \\ T h e r e f o r e, \\ \begin{array}{l} sin θ = y -coordinate \\ cos θ = x -coordinate \\ tan θ = \frac{y -coordinate}{x -coordinate} \end{array} \end{array}

(C) A Cartesian plane is divided into four parts called quadrants by the x-axis and the y-axis. The quadrants are named as first quadrant, second quadrant, third quadrant and fourth quadrant in the anticlockwise direction.

Quick recall:

All – Add

Sine – Sugar

Tangent – To

Cosine – Coffee

Example:

Determine whether the value of each of the following is positive or negative.

(a) sin 105^o (b) cos 75^o (c) tan 305^o (d) sin 50^o

(e) cos 160^o (f) tan 220^o (g) cos 260^o (h) cos 350^o

Solution:

(a) sin 105^o is positive because 90^o< 105^o< 180^o (in second quadrant).

(b) cos 75^o is positive because 0^o< 75^o< 90^o (in first quadrant).

(c) tan 305^o is negative because 270^o< 305^o< 360^o (in fourth quadrant).

(d) sin 50^o is positive because 0^o< 50^o< 90^o (in first quadrant).

(e) cos 160^o is negative because 90^o< 160^o< 180^o (in second quadrant).

(f) tan 220^o is positive because 180^o< 220^o< 270^o (in third quadrant).

(g) cos 260^o is negative because 180^o< 260^o< 270^o (in third quadrant).

(h) cos 350^o is positive because 270^o< 350^o< 360^o (in fourth quadrant).

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

In the diagram above, WZY is a straight line.

∠ X Y Z = 90^{o}, ∠ X W Z = 30^{o}

and WZ = XZ = 30 cm. Find the length of XY.

Solution:

\begin{array}{l} ∠ W X Z = ∠ X W Z = 30^{o} \\ ∴ ∠ X Z Y = 30^{o} + 30^{o} = 60^{o} \\ \sin ∠ X Z Y = \frac{X Y}{X Z} \\ \sin 60^{o} = \frac{X Y}{30} \\ X Y = \sin 60^{o} \times 30 \\ X Y = 25.98 c m \end{array}

Question 5:

In the diagram above, PQS is a right angle triangle. Given that SR = 6cm, PQ = 12 cm and 5SR = 2PS. Find the value of cos α and tan β.

Solution:

\begin{array}{l} 5 S R = 2 P S \\ P S = \frac{5}{2} S R \\ P S = \frac{5}{2} (6) \\ P S = 15 c m \\ \cos α = \frac{P Q}{P S} \\ \cos α = \frac{12}{15} = \frac{4}{5} \\ In △ P Q S, using Pythagoras' Theorem, \\ Q S = \sqrt{P S^{2} - P Q^{2}} \\ Q S = \sqrt{15^{2} - 12^{2}} = 9 c m \\ \tan β = - \tan ∠ P S Q \leftarrow \begin{array}{l} Since 90^{\circ} < β < 180^{\circ} \\ (in quadrant II), tan β is negative \end{array} \\ \tan β = - \frac{P Q}{Q S} \\ \tan β = - \frac{12}{9} = - \frac{4}{3} \end{array}

Question 6:

In the diagram above, ADC is a straight line, if

\sin q = \frac{3}{5} and \tan p = \frac{1}{2}

. Find the distance of AC.

Solution:

\begin{array}{l} Given \sin q = \frac{B D}{A B} = \frac{3}{5} \\ \frac{B D}{30} = \frac{3}{5} \\ B D = \frac{3}{5} \times 30 \\ B D = 18 c m \\ In △ A B D, using Pythagoras' Theorem, \\ A D = \sqrt{A B^{2} - B D^{2}} \\ A D = \sqrt{30^{2} - 18^{2}} = 24 c m \\ Given tan p = \frac{B D}{D C} = \frac{1}{2} \\ \frac{18}{D C} = \frac{1}{2} \\ D C = 36 c m \\ Hence, distance of A C = 24 + 36 = 60 c m . \end{array}

9.1 Values of Sine, Cosine and Tangent of an Angle (Part 2)

Posted on April 23, 2020 by user

(A) Special Angle

(B) Finding the Angles between 0^oand 360^o Given Values of sin θ, cos θ or tan θ

1. If the value of sin θ, cos θ or tan θ is given and 0^o< θ < 360^o, the value of θ can be found using the following steps.

(a) Find the basic angle in first quadrant which corresponds to θ.

(b) Based on the sign of the value of sin θ, cos θ or tan θ, determine the quadrants in which θ lies.

(c) Find the values of θ in the right quadrants found in (b).

Example:

For each of the following cases, find the value of θ.

(a) sin θ = 0.6025 and 90^o< θ < 180^o

(b) cos θ = –0.6025 and 180^o< θ < 270^o

(c) sin θ = –0.8387 and 0^o< θ < 360^o

(d) tan θ = –1.732 and 0^o< θ < 360^o

Solution:

(a)

sin θ = 0.6025

Basic ∠ = 37.05^o ← (Press SHIFT sin^-1 0.6025 =Display: 37.04976)
∴ θ = 180^o – 37.05^o= 142.95^o ← (90^o< θ < 180^o)

(b)

cos θ = –0.6025

Basis ∠ = 52.95^o ← (Press SHIFT cos^-1 0.6025 = Display: 52.9508)

∴ θ = 180^o + 52.95^o= 232.95^o ← (180^o< θ < 270^o)

(c)

sin θ = –0.8387 ← (sin θ is negative in 3^rd quadrant and 4^thquadrant)

Basis ∠ = 57^o ← (Press SHIFT sin^-1 0.8387 = Display: 57.003)

θ₁ = 180^o + 57^o = 237^o ← (180^o< θ < 270^o)

θ₂ = 360^o – 57^o = 303^o ← (270^o< θ < 360^o)

∴ θ = 237^oand 303^o

(d)

tan θ = –1.732 ← (tan θ is negative in 2^nd quadrant and 4^thquadrant)

Basis ∠ = 60^o ← (Press SHIFT tan^-1 1.732 = Display: 59.9993)

θ₁ = 180^o – 60^o = 120^o ← (90^o< θ < 180^o)

θ₂ = 360^o – 60^o = 300^o ← (270^o< θ < 360^o)
∴ θ = 120^oand 300^o

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

In the diagram above, find the value of tan θ.

Solution:

\begin{array}{l} In △ A B C, using Pythagoras' Theorem, \\ A C = \sqrt{1^{2} + 1^{2}} = \sqrt{2} c m \\ \tan θ = \frac{C D}{A C} \\ \tan θ = \frac{1}{\sqrt{2}} \end{array}

Question 2:

In the diagram above, ABCE is a rectangle and point D lies on the straight line EC. Given that DC = 5 cm and AE = 4cm, find the value of cosθ.

Solution:

\begin{array}{l} A D = D C = 5 c m \\ In △ A E D, using Pythagoras' Theorem, \\ E D = \sqrt{5^{2} - 4^{2}} = 3 c m \\ \cos θ = - \cos ∠ A D E \leftarrow \begin{array}{l} Since 90^{\circ} < θ < 180^{\circ} \\ (in quadrant II), \cos θ is negative \end{array} \\ \cos θ = - \frac{E D}{A D} \\ \cos θ = - \frac{3}{5} \end{array}

Question 3:

In the diagram above, PMR is a straight line, M is the midpoint of line PR. Given that QR = 12cm and sin y°= 0.6, find the value of tan x°.

Solution:

\begin{array}{l} In triangle Q M R, \\ \sin y^{\circ} = 0.6 \\ \sin y^{\circ} = \frac{Q R}{Q M} = \frac{6}{10} \\ Given Q R = 12 c m, ∴ Q M = 10 \times 2 = 20 c m \\ In △ Q M R, using Pythagoras' Theorem, \\ M R = \sqrt{20^{2} - 12^{2}} = 16 c m \\ P R = 16 \times 2 = 32 c m \\ Hence \tan x^{\circ} = \frac{Q R}{P R} = \frac{12}{32} = \frac{3}{8} \end{array}

8.2 Angle between Tangent and Chord

Posted on April 23, 2020 by user

8.2 Angle between Tangent and Chord

1. In the diagram above, ABC is a tangent to the circle at point B.

2. Chord PB divides the circle into two segments, that is, the minor segment PRB and the major segment PQB.

3. With respect to ∠PBA, ∠PQB is known as the angle subtended by chord BP in the alternate segment.

4. With respect to ∠QBC, ∠BPQ is known as the angle subtended by chord BQ in the alternate segment.

5. The angle formed by the tangent and the chord which passes through the point of contact of the tangent is the same as the angle in the alternate segment which is subtended by the chord.

6. The relationships between the angles are:

Angle ∠ABP = Angle ∠BQP

Angle ∠CBQ = Angle ∠BPQ