5.7 SPM Practice (Long Questions 3)

Posted on April 23, 2020 by user

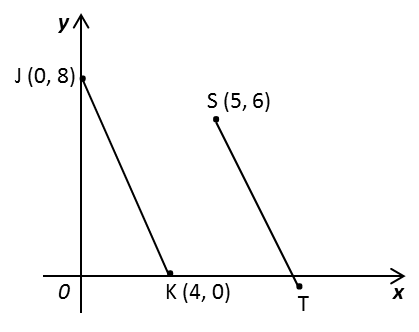
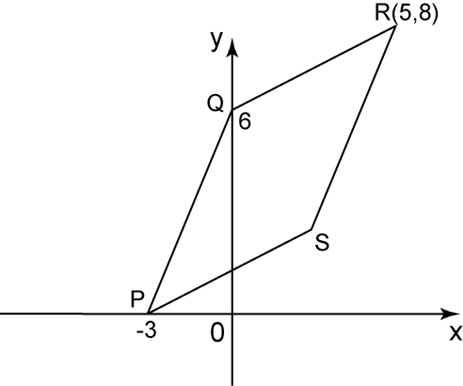
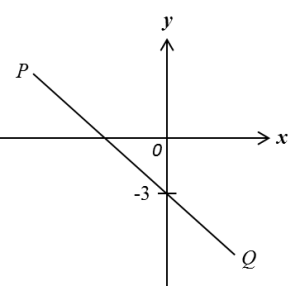
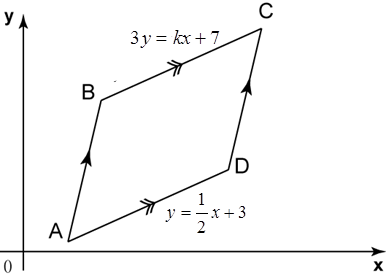
Question 5:

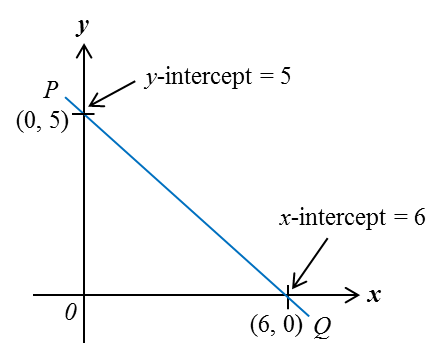
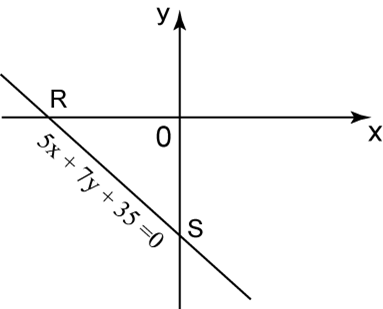
In the diagram above, a straight line 5x + 7y + 35 = 0 intersects with the x-axis and y-axis at R and S respectively. Determine

(a) the gradient of the straight line RS.

(b) the x-intercept of the straight line RS.

(c) the distance of RS.

Solution:
(a)

\begin{array}{l} 5 x + 7 y + 35 = 0 \\ 7 y = - 5 x - 35 \\ y = - \frac{5}{7} x - 5 \\ ∴ The gradient of the straight line R S = - \frac{5}{7} . \end{array}

(b)

\begin{array}{l} At x-intercept, y = 0 \\ 0 = - \frac{5}{7} x - 5 \\ \frac{5}{7} x = - 5 \\ x = - 7 \\ ∴ x-intercept of the straight line R S = - 7. \end{array}

(c)

\begin{array}{l} Point R = (- 7, 0) and point S = (0, - 5) \\ Distance of R S = \sqrt{{(- 7 - 0)}^{2} + {(0 - (- 5))}^{2}} \\ Distance of R S = \sqrt{49 + 25} \\ Distance of R S = \sqrt{74} units \end{array}

Question 6:

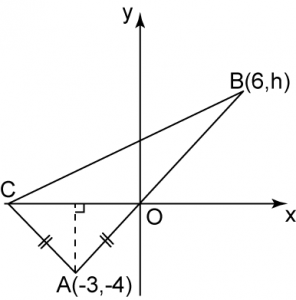
In the diagram above, O is the origin of the Cartesian plane, AOB is a straight line and OA = AC. Find

(a) the coordinates of C.

(b) the value of h.

(c) the equation of BC.

Solution:
(a)

x-coordinate of C = –3 × 2 = –6

Therefore coordinates of C = (–6, 0).

(b)

\begin{array}{l} Gradient of A O = Gradient of O B \\ \frac{0 - (- 4)}{0 - (- 3)} = \frac{h - 0}{6 - 0} \\ \frac{4}{3} = \frac{h}{6} \\ h = 8 \end{array}

(c)

\begin{array}{l} Gradient of B C = \frac{8 - 0}{6 - (- 6)} = \frac{8}{12} = \frac{2}{3} \\ At point C (- 6, 0), \\ 0 = \frac{2}{3} (- 6) + c \\ c = 4 \\ The equation of B C is, \\ y = \frac{2}{3} x + 4 \end{array}

5.2 Gradient of a Straight Line in Cartesian Coordinates

Posted on April 23, 2020 by user

5.2 Finding the Gradient of a Straight Line

The gradient, m, of a straight line which passes through P (x₁, y₁) and Q (x₂, y₂) is given by,

m_PQ =

\frac{y_{2} - y_{1}}{x_{2} - x_{1}}

Example 1:

Find the gradient of the straight line joining two points P and Q in the above diagram.

Solution:

P = (x₁, y₁) = (4, 3), Q = (x₂, y₂) = (10, 5)

Gradient of the straight line PQ

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{5 - 3}{10 - 4} \\ = \frac{2}{6} = \frac{1}{3} \end{array}

Example 2:

Calculate the gradient of a straight line which passes through point A (7, -3) and point B (-3, 6).

Solution:

A = (x₁, y₁) = (7, -3), B = (x₂, y₂) = (-3, 6)

Gradient of the straight line AB

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{6 - (- 3)}{- 3 - 7} \\ = - \frac{9}{10} \end{array}

5.7 SPM Practice (Long Questions 2)

Posted on April 23, 2020 by user

Question 3:

Diagram below shows a straight line JK and a straight line ST drawn on a Cartesian plane. JK is parallel to ST.

Find

(a) the equation of the straight ST,

(b) the x-intercept of the straight line ST.

Solution:

(a)
JK is parallel to ST, therefore gradient of JK = gradient of ST.

\begin{array}{l} = \frac{8 - 0}{0 - 4} \\ = - 2 \end{array}

Substitute m = –2 and S (5, 6) into y = mx + c

6 = –2 (5) + c

c = 16

Therefore equation of ST: y = –2x + 16

(b)
For x-intercept, y = 0

0 = –2x + 16

2x = 16

x = 8

Therefore x-intercept of ST = 8

Question 4:

In the diagram above, PQRS is a parallelogram. Find

(a) the gradient of SR,

(b) the equation of QR,

(c) the x-intercept of QR.

Solution:

(a)
PQ is parallel to SR, gradient of PQ = gradient of SR.

Gradient of S R = - \frac{6}{- 3} = 2

(b)

\begin{array}{l} Gradient of Q R = \frac{8 - 6}{5 - 0} = \frac{2}{5} \\ Substitute m = \frac{2}{5} and R (5, 8) into y = m x + c \\ 8 = \frac{2}{5} (5) + c \\ c = 6 \\ Therefore equation of Q R : y = \frac{2}{5} x + 6 \end{array}

(c)

\begin{array}{l} For x-intercept, y = 0 \\ 0 = \frac{2}{5} x + 6 \\ x = - 15 \end{array}

Therefore x-intercept of QR = –15.

5.6 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

Diagram below shows a straight line RS on a Cartesian plane.

Find the gradient of RS.

Solution:

\begin{array}{l} Using gradient formula \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ Gradient of R S = \frac{3 - 1}{5 - (- 1)} = \frac{2}{6} = \frac{1}{3} \end{array}

Question 2:

In diagram below, PQ is a straight line with gradient

- \frac{1}{2}

Find the x-intercept of the straight line PQ.

Solution:

\begin{array}{l} Using the gradient formula, m = - \frac{y-intercept}{x-intercept} \\ - \frac{1}{2} = - (\frac{- 3}{x-intercept}) \\ x-intercept = 3 \times (- 2) = - 6 \end{array}

Question 3:

Diagram below shows a straight line RS drawn on a Cartesian plane.

It is given that the distance of RS is 10 units.

Find the gradient of RS.

Solution:

\begin{array}{l} R S = 10 units, O S = 6 units \\ O R = \sqrt{10^{2} - {(- 6)}^{2}} = 8 units \\ y-intercept of R S = - 6 \\ x-intercept of R S = - 8 \\ Using the gradient formula, m = - \frac{y-intercept}{x-intercept} \\ ∴ Gradient of R S = - (\frac{- 6}{- 8}) = - \frac{3}{4} \end{array}

Question 4:

The gradient of the straight line 3x – 4y = 24 is

Solution:

Rearrange the equation in the form y = mx+ c

3x – 4y = 24

4y = 3x – 24

y = \frac{3}{4} x - 6

Therefore, gradient of the straight line =

\frac{3}{4} .

Question 5:

Determine the y-intercept of the straight line 3x + 2y = 5

Solution:

For y-intercept, x = 0

3(0) + 2y = 5

\begin{array}{l} y = \frac{5}{2} \\ ∴ y -intercept = \frac{5}{2} . \end{array}

5.7 SPM Practice (Long Questions 1)

Posted on April 23, 2020 by user

Question 1:

In diagram below, ABCD is a trapezium drawn on a Cartesian plane. BC is parallel to AD and O is the origin. The equation of the straight line BC is 3y = kx+ 7 and the equation of the straight line AD is

y = \frac{1}{2} x + 3

Find

(a) the value of k,

(b) the x-intercept of the straight line BC.

Solution:
(a)

Equation of BC :

3y = kx + 7

\begin{array}{l} y = \frac{k}{3} x + \frac{7}{3} \\ ∴ Gradient of B C = \frac{k}{3} \\ Equation of A D : y = \frac{1}{2} x + 3 \\ ∴ Gradient of A D = \frac{1}{2} \\ Gradient of B C = gradient of A D \\ \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}

Gradient of BC = gradient of AD

\begin{array}{l} \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}

(b)
Equation of BC,

3 y = \frac{3}{2} x + 7

For x-intercept, y = 0

\begin{array}{l} 3 (0) = \frac{3}{2} x + 7 \\ \frac{3}{2} x = - 7 \\ x = - \frac{14}{3} \end{array}

Therefore x-intercept of BC =

- \frac{14}{3}

Question 2:

In diagram below, O is the origin. Straight line MN is parallel to a straight line OK.

Find

(a) the equation of the straight line MN,

(b) the x-intercept of the straight line MN.

Solution:

(a)
Gradient of MN = gradient of OK

Gradient of MN

\begin{array}{l} = \frac{5 - 0}{3 - 0} \\ = \frac{5}{3} \end{array}

Substitute m = 5/3 and (–2, 5) into y = mx + c

5 = \frac{5}{3} (- 2) + c

15 = – 10 + 3c

3c = 25

c = 25/3

Therefore equation of MN:

y = \frac{5}{3} x + \frac{25}{3}

(b)

For x-intercept, y = 0

\begin{array}{l} 0 = \frac{5}{3} x + \frac{25}{3} \\ \frac{5}{3} x = - \frac{25}{3} \end{array}

5x = –25

x = –5

Therefore x-intercept of MN = –5

5.3 Intercepts (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

The x-intercept of the line ST is

Solution:

The x-coordinate for the point of intersection of the straight line with x-axis is -0.4.

Therefore the x-intercept of the line ST is –0.4.

Example 2:

Find the x-intercept of the straight line 2x + 3y + 6 = 0.

Solution:

2x + 3y + 6 = 0

At x-intercept, y = 0

2x + 3(0) + 6 = 0

2x = –6

x = –3

Example 3:

What is the y-intercept of the straight line 12x – 15y = 60?

Solution:

12x – 15y = 60

At y-intercept, x = 0

12(0) – 15y = 60

– 15y = 60

y = –4

5.3 Intercepts

Posted on April 23, 2020 by user

5.3 Intercepts

1. The x-intercept is the point of intersection of a straight line with the x-axis.

2. The y-intercept is the point of intersection of a straight line with the y-axis.

3. In the above diagram, the x-intercept of the straight line PQ is 6 and the y-intercept of PQ is 5.

4. If the x-intercept and y-intercept of a straight line are given,

Gradient, m = - \frac{y - intercept}{x - intercept}

5.1 Gradient of a Straight Line

Posted on April 23, 2020 by user

5.1 Gradient of a Straight Line

The gradient of a straight line is the ratio of the vertical distance to the horizontal distance between any two given points on the straight line.

Gradient, m = \frac{Vertical distance}{Horizontal distance}

Example:

Find the gradient of the straight line above.

Solution:

\begin{array}{l} Gradient, m = \frac{Vertical distance}{Horizontal distance} \\ = \frac{4 units}{6 units} \\ = \frac{2}{3} \end{array}

5.2 Gradient of a Straight Line in Cartesian Coordinates (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Given that a straight line passes through points (-3, -7) and (4, 14). What is the gradient of the straight line?

Solution:

Let (x₁, y₁) = (-3, -7) and (x₂, y₂) = (4, 14).

Gradient of the straight line

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{14 - (- 7)}{4 - (- 3)} \\ = \frac{21}{7} = 3 \end{array}

Example 2:

The gradient of the straight line PQ in the diagram above is

Solution:

Let (x₁, y₁) = (12, 0) and (x₂, y₂) = (0, 7).

Gradient of the straight line PQ

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{7 - 0}{0 - 12} \\ = - \frac{7}{12} \end{array}

Example 3:

A straight line with gradient -3 passes through points (-4, 6) and (-1, p). Find the value of p.

Solution:

\begin{array}{l} \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = - 3 \\ \frac{p - 6}{- 1 - (- 4)} = - 3 \\ \frac{p - 6}{3} = - 3 \\ p - 6 = - 9 \\ p = - 3 \end{array}

5.4 Equation of a Straight Line (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Given that the equation of a straight line is 4x + 6y – 3 = 0. What is the gradient of the line?

Solution:

4x + 6y – 3 = 0

6y = – 4x + 3

\begin{array}{l} y = - \frac{4 x}{6} + \frac{3}{6} \\ y = - \frac{2}{3} x + \frac{1}{2} \\ y = m x + c \\ g r a d i e n t, m = - \frac{2}{3} \end{array}

Example 2:

Given that the equation of a straight line is y = – 7x + 3. Find the y-intercept of the line?

Solution:

y = mx + c, c is y-intercept of the straight line.

Therefore for the straight line y = – 7x + 3,

y-intercept is 3

Example 3:

Find the equation of the straight line MN if its gradient is equal to 3.

Solution:

Given m = 3

Substitute m = 3 and (-2, 5) into y = mx + c.

5 = 3 (-2) + c

5 = -6 + c

c = 11

Therefore the equation of the straight line MN is y = 3x + 11