Home › Archive for SPM Maths › Page 21

SPM Maths

5.4 Equation of a Straight Line

Posted on by

5.4 Equation of a Straight Line: y = mx + c

1. Given the value of the gradient, m, and the y-intercept, c, an equation of a straight line
y = mx + c can be formed.

2. If the equation of a straight line is written in the form y = mx + c, the gradient, m, and the y-intercept, c, can be determined directly from the equation.

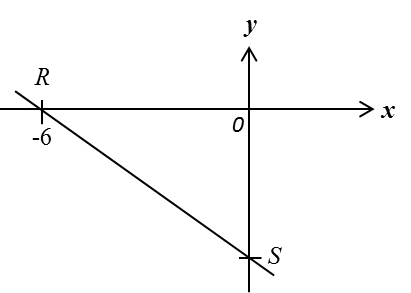
Example:
Given that the equation of a straight line is y = 3 – 4x. Find the gradient and y-intercept of the line?
 
Solution:
y= 3 – 4x
y= – 4x + 3 ← (y = mx + c)
Therefore, gradient, m = – 4
y-intercept, c = 3



3. If the equation of a straight line is written in the form ax + by + c = 0, change it to the form y = mx + c before finding the gradient and the y-intercept.

Example:
Given that the equation of a straight line is 4x + 6y– 3 = 0. What is the gradient and y-intercept of the line?

Solution:
4x + 6y – 3 = 0
6y = –4x + 3

y=− 2 3 x+ 1 2 ← y=mx+c ∴ Gradient m=− 2 3      y−intercept, c= 1 2
 

5.5 Parallel Lines (Sample Questions)

Posted on by

Example 1:

















The straight lines MN and PQ in the diagram above are parallel. Find the value of q.

Solution:
If two lines are parallel, their gradients are equal.
m1 = m2
mMN = mPQ

using gradient formula y 2 − y 1 x 2 − x 1 9 − 4 5 − ( − 1 ) = q − ( − 5 ) 5 − ( − 7 ) 5 6 = q + 5 12
60 = 6q + 30
6q = 30
q = 5

5.5 Parallel Lines (Part 1)

Posted on by
5.5 Parallel Lines (Part 1)
 
(A) Gradient of parallel lines

1. Two straight lines are 
parallel if they have
the same gradient.
If PQ // RS,
then mPQ = mRS
   
2. If two straight lines have 
the same gradient, then  
they are parallel. 
If mAB = mCD
then AB // CD


Example 1:
Determine whether the two straight lines are parallel.
(a) 2y – 4x = 6
  y = 2x – 5
(b) 2y = 3x –4
  3y = 2x +12
 
Solution:
(a) 
2y – 4x = 6
2y = 6 + 4x
y = 2x + 3,   m1= 2
y = 2x – 5,   m2 = 2
m1= m2
Therefore, the two straight lines are parallel.
 
(b)
2y=3x−4 y= 3 2 x−2,    m 1 = 3 2 3y=2x+12 y= 2 3 x+4,    m 2 = 2 3 m 1 ≠ m 2 ∴ The two straight lines are not parallel.

5.6 SPM Practice (Short Questions)

Posted on by

5.6.2 The Straight Line, SPM Paper 1 (Short Questions)

Question 6:
Diagram below shows a straight line RS with equation 3y = –px – 12, where p is a constant.
 

It is given that OR: OS = 3 : 2.
Find the value of p.

Solution:
Method 1:
Substitute x= –6 and y = 0 into 3y = –px – 12:
3(0) = –p (–6) – 12
0 = 6p – 12
–6p = –12
p = 2

Method 2:
OR: OS = 3 : 2
O R O S = 3 2 6 O S = 3 2 O S = 6 × 2 3 = 4 units  

Coordinates of S = (0, –4)
Gradient of the straight line RS = − − 4 − 6 = − 2 3  

Given 3y = –px – 12
Rearrange the equation in the form y = mx + c
y = − p 3 x − 4 Gradient of the straight line R S = − P 3 ∴ − P 3 = − 2 3 P = 2



Question 7:

 
The above diagram shows two straight lines, KL and LM, on a Cartesian plane. The distance KL is 10 units and the gradient of LM is 2. Find the x-intercept of LM.

Solution:


Let point N be = (0, 2).
Using Pythagoras’ Theorem,
 LN = √102 – 62 = 8
Point L = (0, 2 + 8) = (0, 10)
y-intercept of LM = 10
 
Using the gradient formula, m = − y-intercept x-intercept 2 = − ( 10 x-intercept ) x-intercept of L M = − 10 2 = − 5  

4.3 Operations on Statements (Sample Questions 1)

Posted on by

Example 1:
Form a compound statement by combining two given statements using the word ‘and’.
(a) 3 × 12 = 36
 7 × 5 = 35

(b) 5 is a prime number.
 5 is an odd number.

(c) Rectangles have 4 sides.
 Rectangles have 4 vertices.

Solution:
(a) 3 × 12 = 36 and 7 × 5 = 35
(b) 5 is a prime number and an odd number.
(c) Rectangles have 4 sides and 4 vertices.



Example 2:
Form a compound statement by combining two given statements using the word ‘or’.
(a) 16 is a perfect square. 16 is an even number.
(b) 4 > 3.  -5 < -1

Solution:
(a) 16 is a perfect square or an even number.
(b) 4 > 3 or -5 < -1.

4.1 Statements (Sample Questions)

Posted on by

Example 1:
Determine whether the following sentences are statements or not. Give a reason for your answer.
(a) 3 + 3 = 8
(b) 9 – 4 = 5
(c) A pentagon has 5 sides.
(d) 4 is a prime number.
(e) Is 40 divisible by 3?
(f) Find the perimeter of a square with each side of 4 cm.
(g) Help!

Answer:
(a) Statement; it is a false statement.
(b) Statement; it is a true statement.
(c) Statement; it is a true statement.
(d) Statement; it is a false statement.
(e) Not a statement; it is a question.
(f) Not a statement; it is an instruction.
(g) Not a statement; it is an exclamation.





Deduction and Induction

Posted on by
4.6 Deduction and Induction

(A) Reasoning by Deduction and Induction
1. Reasoning by deduction is a process of making a conclusion for a specific case based on a given general statement.

2. Reasoning by induction is a process of making a generalization based on specific cases.

Maths Tip
1. General statement  →  Special conclusion  → Deduction
2. Specific cases  →  General conclusion  →  Induction
Example: 
Determine whether the following conclusion is made based on a deductive reasoning or inductive reasoning.

(a) Area of triangle = ½ × Base × Height
(i) 

Area of ∆ ABC
= ½ × 7cm × 5cm
= 17.5 cm2 
  
(ii)

Area of ∆ DEF
= ½ × 7cm × 4cm
= 14 cm2
  
(b)
1 = 7 (1)2 – 6
22 = 7 (2)2 – 6
57 = 7 (3)2 – 6
106 = 7 (4)2 – 6
 7n2 – 6, n = 1, 2, 3, 4…
 
Solution: 
(a)
The specific conclusion is made based on a general statement ~ Area of triangle = ½ × Base × Height. Therefore, the conclusion is made based on deductive reasoning.

(b) 
The general conclusion 7n2 – 6, n = 1, 2, 3, 4… is made based on specific cases. Therefore, the conclusion is based on inductive reasoning.

4.6 SPM Practice (Long Questions)

Posted on by

Question 1:
(a) State if each of the following statements is true or false.
 (i) (i)  2 4 =16  and  12÷ 27 3 =3.
 (ii) 17 is a prime number or an even number.

(b) Complete the statement, in the answer space, to form a true statement by using the quantifier ‘all’ or ‘some’.

(c) Write down two implications based on the following statement:

A number is a prime number if and only if it is only divisible by 1 and itself.
Solution:
(a)(i) False
(a)(ii) True

(b)   Some   multiples of 3 are multiples of 6.

(c) Implication 1: If a number is a prime number, then it is only divisible by 1 and itself.
 Implication 2: If a number is only divisible by 1 and itself, then it is a prime
 number.


Question 2:
(a) State if each of the following statements is true or false.
  (i)  2 × 3 = 6 or 2 + 3 = 6
  (ii) 2 is a prime number and 5 is an even number.

(b) Write down the converse of the following implication.
  Hence, state whether the converse is true or false.

If x is a multiple of 12,
then x is a multiple of 3.
(c) Complete the premise in the following argument:

Premise 1: All hexagons have six sides
Premise 2: _____________________
Conclusion: ABCDEF has six sides.
Solution:
(a)(i) True
(a)(ii) False

(b) Converse: If x is a multiple of 3, then x is a multiple of 12.
  The converse is false.

(c) Premise 2: ABCDEF is a hexagon.

4.6 SPM Practice (Long Questions)

Posted on by

Question 3:
(a) Complete each of the following statements with the quantifier ‘all’ or ‘some’ so that it will become a true statement.
  (i) ___________ of the prime numbers are odd numbers.
 (ii) ___________ pentagons have five sides.

(b) Write down two implications based on the following statement:

A ∩ B = B if and only if A υ B = A.
(c) Complete the premise in the following argument:

Premise 1: If a number is a factor of 24, then it is a factor of 48.
Premise 2: 12 is a factor of 24.
Conclusion: _____________________

Solution:
 (a)(i)    Some  of the prime numbers are odd numbers.
 (a)(ii)  All pentagons have five sides.

(b) Implication 1: If A ∩ B = B, then A υ B = A.
  Implication 2: If A υ B = A, then A ∩ B = B.

(c) Conclusion: 12 is a factor of 48.


Question 4:
(a) Combine the following two statements to form one true statement.
  Statement 1: (– 3)² = 9
  Statement 2: –3 (3) = 19
(b) Complete the premise in the following argument:

Premise 1: _____________________
Premise 2: x is a multiple of 25.
Conclusion: x is a divisible of 5.
(c) Make a general conclusion by induction for the sequence of numbers 7, 14, 27, … which follows the following pattern.
7 = 3 (2)1 + 1
14 = 3 (2)2 + 2
27 = 3 (2)3 + 3
…. = ………..
Solution:
(a) (– 3)² = 9 or –3 (3) = 19.

(b) Premise 1: All multiples of 25 is divisible by 5.

(c) 3 (2)n + n, where n = 1, 2, 3, …

4.2 Quantifiers ‘All’ and ‘Some’ (Sample Questions)

Posted on by

Example 1:
Complete each of the following statements using the quantifiers ‘all’ or ‘some’ to make the statement true.
(a) _____ rectangles are squares.
(b) _____ prime numbers are odd numbers.
(c) _____ triangles have equal sides.
(d) _____ even numbers are divisible by 2.

Answer:
(a) Some rectangles are squares.
(b) Some prime numbers are odd numbers.
(c) Some triangles have equal sides.
(d) All even numbers are divisible by 2.



Example 2:
Construct a true statement using the quantifier ‘all’ or ‘some’ for the given object and property.
(a) Object: multiples of 4
 Property: can be divided exactly by 5
(b) Object: regular hexagon
 Property: 6 equal sides
(c) Object: acute angles
 Property: less than 90o

Answer:
(a) Some multiples of 4 can be divided exactly by 5.
(b) All regular hexagons have 6 equal sides.
(c) All acute angles are less than 90o.