Home › Archive for SPM Maths › Page 24

SPM Maths

Quadratic Equations Long Questions (Question 5 – 7)

Posted on by
Question 5:
Solve the equation:
(m + 2)(m – 4) = 7(m – 4).
 
Solution:
(m + 2)(m – 4) = 7(m – 4)
m2– 4m + 2m – 8 = 7m – 28
m2– 9m + 20 = 0
(m – 5)(m – 4) = 0
m = 5 or m = 4   


Question 6:
Solve the equation:
− 6 y − 2 y = 7 1 − y

Solution:
−6y−2 y = 7 1−y ( −6y−2 )( 1−y )=7y −6y+6 y 2 −2+2y−7y=0 6 y 2 −11y−2=0 ( 6y+1 )( y−2 )=0 6y+1=0        or        y=2 y=− 1 6


Question 7:
Solve the equation:
4 m 7 = m ( 8 m − 9 )

Solution:
4m 7 =m( 8m−9 ) 4m=7m( 8m−9 ) 4m=56 m 2 −63m 56 m 2 −63m−4m=0 56 m 2 −67m=0 m(56m−67)=0 m=0        or        56m−67=0                                        m= 67 56

2.4 Roots of Quadratic Equations

Posted on by

2.4 Roots of Quadratic Equations
1. A root of quadratic equation is the value of the unknown which satisfies the quadratic equation.

2. Roots of an equation are also called the solution of an equation.

3. To solve a quadratic equation by the factorisation method, follow the steps below:

Step 1: Express the quadratic equation in general form ax2 + bx + c = 0.
Step 2: Factorise the quadratic expression ax2 + bx + c = 0 as the product of two linear expressions, that is, (mx+ p) (nx + q) = 0.
Step 3: Equate each factor to zero and obtain the roots or solutions of the quadratic equation.

mx+p=0      or      nx+q=0     x=− p m       or          x=− q n


Example 1:
Solve the quadratic equation  2 x 2 − 5 3 = 3 x

Solution:
2 x 2 − 5 3 = 3 x
2x2 – 5 = 9x
2x2 – 9x – 5 = 0
(x – 5)(2x + 1) = 0
x – 5 = 0, x = 5
or 2x + 1 = 0
x = − 1 2  
Therefore, x = 5 and x = ½ are roots or solutions of the quadratic equation.


Example 2:
Solve the quadratic equation 4x2 – 12 = –13x
 
Solution:
4x2 – 12 = –13x
4x2 + 13x – 12 = 0
(4x – 3)(x + 4) = 0
4x – 3 = 0,  x = 3 4
or x + 4 = 0
x = –4


Example 3:
Solve the quadratic equation 5x2 = 3 (x + 2) – 4

Solution:
5x2 = 3 (x + 2) – 4
5x2 = 3x + 6 – 4
5x2 – 3x – 2 = 0
(5x + 2)(x – 1) = 0
5x + 2 = 0,  x = − 2 5
or x – 1 = 0
x = 1


Example 4:
Solve the quadratic equation 
3 x ( x − 3 ) 4 = − x + 3.
 
Solution:
3 x ( x − 3 ) 4 = − x + 3
3x2 – 9x = – 4x + 12
3x2 – 5x – 12 = 0
(3x + 4)(x – 3) = 0
3x + 4 = 0,  x = − 4 3
or x – 3 = 0
x = 3

2.1 Quadratic Expression (Sample Questions)

Posted on by

Example 1:
Form a quadratic expression by multiplying each of the following.
(a) (6p – 2)(2p – 1)
(b)   (m + 5)(4 – 7m)
(c)    (x + 2) (2x – 3)

Solution:
(a) (6p – 2)(2p – 1)
= (6p)(2p) + (6p)(-1) + (-2)(2p) +(-2)(-1)
= 12p2 – 6p – 4p + 2
= 12p2 – 10p + 2

(b) (m + 5)(4 – 7m)
= (m)(4) + (m)(-7m) + (5)(4) + (5)(-7m)
= 4m – 7m2 + 20 – 35m
= – 7m2 – 31m+ 20

(c) (x + 2) (2x – 3)
= (x)(2x) + (x)(-3) + (2)(2x) + (2)(-3)
= 2x2-3x + 4x – 6
= 2x2 + x - 6

Quadratic Equations Long Questions (Question 8 – 10)

Posted on by
Question 8:
Solve the following quadratic equation:
4x (x + 4) = 9 + 16x

Solution:
4x( x+4 )=9+16x 4 x 2 +16x=9+16x    4 x 2 −9=0 ( 2x ) 2 − 3 2 =0 ( 2x+3 )( 2x−3 )=0 2x+3=0     or     2x−3=0      2x=−3                2x=3        x=− 3 2                  x= 3 2    


Question 9:
Solve the following quadratic equation:
(x + 2)2 = 2x + 7

Solution:
( x+2 ) 2 =2x+7 x 2 +4x+4=2x+7 x 2 −2x−3=0 ( x+1 )( x−3 )=0 x+1=0     or     x−3=0      x=−1                 x=3


Question 10:
Solve the following quadratic equation:
− 2 3x−5 = x 3x−1

Solution:
              − 2 3x−5 = x 3x−1          −2( 3x−1 )=x( 3x−5 )               −6x+2=3 x 2 −5x 3 x 2 −5x+6x−2=0          3 x 2 +x−2=0    ( 3x−2 )( x+1 )=0 3x−2=0     or     x+1=0      3x=2                  x=−1        x= 2 3                  x=−1

2.2 Factorisation of Quadratic Expression

Posted on by
2.2 Factorisation of Quadratic Expression
 
(A) Factorisation quadratic expressions of the form ax2 + bx + c, b = 0 or c = 0
1. Factorisation of quadratic expressions is a process of finding two linear expressions whose product is the same as the quadratic expression.
2. Quadratic expressions ax2 + c and ax2 + bx that consist of two terms can be factorised by finding the common factors for both terms.
 
Example 1:
Factorise each of the following:
(a) 2x2+ 6
(b) 7p2– 3p
(c) 6x2– 9x
 
Solution:
(a) 2x2+ 6 = 2 (x2 + 3) ← (2 is common factor)
(b) 7p2– 3p = p (7p – 3) ← (p is common factor)
(c) 6x2– 9x = 3x (2x – 3) ← (3x is common factor)


(B) Factorisation of quadratic expressions in the form ax2 – c , where a and c are perfect squares
 
Example 2:
(a) 9p2– 16
(b) 25x2– 1
(c) 1 4 − 1 25 x 2

Solution: 
(a) 9p2– 16 = (3p)2 – 42= (3p – 4) (3p + 4)
(b) 25x2– 1 = (5x)2 – 12= (5x – 1) (5x + 1)
(c)
1 4 − 1 25 x 2 = ( 1 2 ) 2 − ( 1 5 x ) 2 = ( 1 2 − 1 5 x ) ( 1 2 + 1 5 x )


(C) Factorisation quadratic expressions in the form ax2 + bx + c, where a ≠ 0, b ≠ 0 and c ≠ 0
 
Example 3:
Factorise each of the following
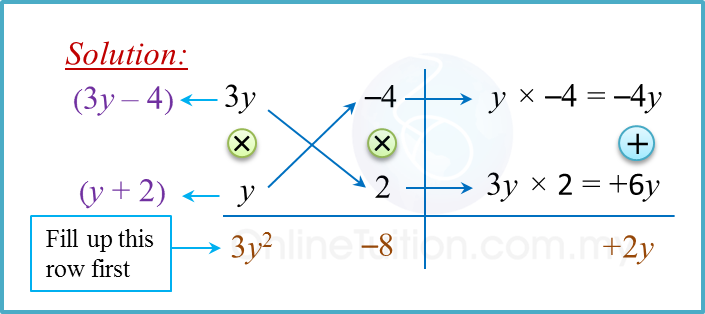
(a) 3y2+ 2y – 8
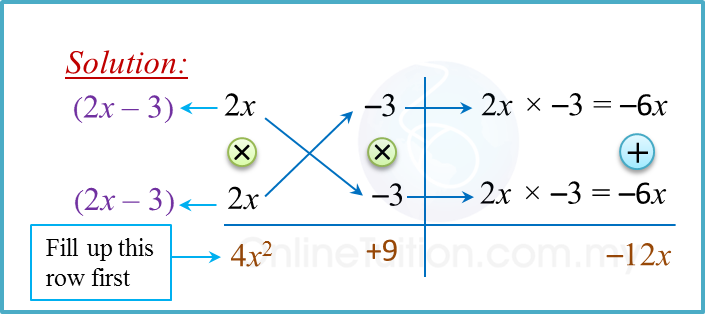
(b) 4x2– 12x + 9
 
Solution: 
(a)
Factorise using the Cross Method
 

3y2+ 2y – 8 = (3y – 4) (y + 2)

(b)

 
 4x2– 12x + 9 = (2x – 3) (2x – 3)
 

2.1 Quadratic Expression

Posted on by
(A) Identifying quadratic expression
1. A quadratic expression is an algebraic expression of the form ax2 + bx + c, where a, b and c are constants, a ≠ 0 and x is an unknown.
(a) The highest power of x is 2.
(b) For example, 5x2– 6x + 3 is a quadratic expression.

Example 1
State whether each of the following is a quadratic expression in one unknown.
(a) x2 – 5x + 3
(b) 8p2 + 10
(c) 5x + 6
(d) 2x2 + 4y + 14
(e)  2 p + 1 p + 6
(f) y3 – 3y + 1

Solution:
(a) Yes. A quadratic expression in one unknown.

(b) Yes. A quadratic expression in one unknown.

(c) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

(d) Not a quadratic expression in one unknown. There are 2 unknowns, x and y in the quadratic expression.

(e) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2. 
1 p = p − 1

(f) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

2. A quadratic expression can be formed by multiplying two linear expressions.
 (2x + 3)(x  - 3) = 2x2 – 3x – 9


Example 2
Multiply the following pairs of linear expressions.
(a) (4x + 3)(x – 2)
(b) (y – 6)2
(c) 2x (x – 5)

Solution:
(a) (4x + 3)(x – 2)
= (4x)(x) + (4x)(-2) +(3)(x) + (3)(-2)
= 4x2 – 8x + 3x – 6
= 4x2 – 5x – 6

(b) (y – 6)2 
= (y – 6)(y – 6)
= (y)(y) + (y)(-6) + (-6)(y) + (-6)(-6)
= y2 -6y – 6y + 36
= y2 - 12y + 36

(c) 2x (x – 5) 
= 2x(x) + 2x(-5)
= 2x2 – 10x

Quadratic Equations Long Questions (Question 1 – 4)

Posted on by

Question 1:
Solve the quadratic equation, (y + 3)(y – 4) = 30

Solution:
(y + 3)(y – 4) = 30
y2 – 4y + 3y– 12 = 30
y2 – y – 12 – 30 = 0
y2 – y – 42 = 0
(y + 6)(y – 7) = 0
y + 6 = 0, y = –6
Or
y – 7 = 0
y = 7


Question 2:
Solve the quadratic equation, 5x2 = 3( x – 2) + 8

Solution:
5x2 = 3x – 6 + 8
5x2 – 3x – 2 = 0
(5x + 2)(x – 1) = 0
5x + 2 = 0, x − 2 5
Or
x – 1 = 0
x = 1


Question 3:
Solve the quadratic equation
2 p 2 − 15 p = 7

Solution:
2 p 2 − 15 p = 7
2p2 – 15 = 7p
2p2 –7p – 15 = 0
(2p + 3)(p – 5) = 0
2p + 3 = 0, p =  − 3 2
Or 
p – 5 = 0
p = 5


Question 4:
Solve the quadratic equation  y ( y − 9 2 ) = 5 2

Solution:
y ( y − 9 2 ) = 5 2 y 2 − 9 y 2 = 5 2

( ×2), 2y2 – 9y= 5
2y2 – 9y – 5 = 0
(2y + 1)(y – 5) = 0
2y + 1 = 0, y = – ½
Or
y – 5 = 0
y = 5

1.3 SPM Practice (Short Questions)

Posted on by

1.3.2 Standard Form, SPM Practice (Paper 1)
Question 6:
(a)  Round off 0.05079 correct to three significant figures.
(b)  Find the value of 5 × 107 + 7.2 × 105 and state its answer in standard form.

Solution:
(a)  0.05079 = 0.0508 (correct to three significant figures)
(b)  5 × 107 + 7.2 × 105 = 500 × 105 + 7.2 × 105
= (500 + 7.2) × 105
= 507.2 × 105
= 5.072 × 107


Question 7:
(a)  Calculate the value of 70.2 – 3.22 × 8.4 and round off its answer correct to three significant figures.
(b)  Express 840 0.000021  as a number in standard form.

Solution:
(a)  70.2 – 3.22 × 8.4 = 70.2 – 27.048
= 43.152 = 43.2 (correct to three significant figures)

(b)   
840 0.000021 = 8.4 × 10 2 2.1 × 10 − 5 = 8.4 2.1 × 10 2 − ( − 5 ) = 4 × 10 7



Question 8:
Calculate the value of 7 × (2 × 10-2)3– 4.3 × 10-5 and state its answer in standard form.

Solution:
7 × (2 × 10-2)3 – 4.3 × 10-5= 7 × 23 × (10-2)3 – 4.3 × 10-5
= 56 × 10-6 – 4.3 × 10-5
= 5.6 × 10-5 – 4.3 × 10-5
= 1.3 × 10-5

1.2 Standard Form (Sample Questions)

Posted on by

Example 1:
Find the value of 7.3 × 103 + 3.2 × 104 and express your answer in standard form.

Solution:
7.3 × 103 + 3.2 × 104
= 7.3 × 103 + 3.2 × 101 × 103
= [7.3 + (3.2 × 101)] × 103
= 39.3 × 103
= 3.93 × 104


Example 2:
Find the value of 3.3 × 105 + 6400 and express your answer in standard form.

Solution:
= 3.3 × 105 + 6.4 × 103
= 3.3 × 101 × 101 × 103+ 6.4 × 103
= 330 × 103 + 6.4 × 103
= (330 + 6.4) × 103
= 336.4 × 103
= 3.364 × 105

1.1 Significant Figures

Posted on by
1.1.2 Significant Figures (Part 2)
1. Perform combined operations (addition, subtraction, multiplication and division) involving numbers, the final answer is rounded off to specific significant figures. 

Example:
Find the value of each of the following and give your answer correct to 3 significant figures.
(a) 261.9 + 75.6 × 0.7
(b) 0.062 × 30.12 + 1.268
(c)  8.608 ÷ 0.08 − 28.35
(d) 0.846 ÷ 0.4 - 0.153 × 2

Solution:
(a) 261.9 + 75.6 × 0.7
= 261.9 + 52.92
= 314.82
= 315 (3 s. f.)

(b) 0.062 × 30.12 + 1.268
= 1.86744 + 1.268
= 3.13544
= 3.14 (3 s. f.)

(c)  8.608 ÷ 0.08 − 28.35
= 107.6 – 28.35
= 79.25
= 79.3 (3 s. f.)

(d)  0.846 ÷ 0.4 − 0.153 × 2
= 2.115 – 0.306
= 1.809
= 1.81 (3 s. f.)



Example 1:
Calculate the value of 5.33 + 0.33 × 17 and give your answer correct to three significant figures.

Solution:
5.33 + 0.33 × 17
= 5.33 + 5.61
= 10.94
= 10.9 (3 s. f.)



Example 2:
Calculate the value of 49.3567 + 16.73 ÷ 0.5 and give your answer correct to four significant figures.
Solution:
49.3567 + 16.73 ÷ 0.5
= 49.3567 + 33.46
= 82.8167
= 82.82 (4 s. f.)



Example 3:
Calculate the value of 3.42 ÷ 12 × 3.7 and give your answer correct to four significant figures.

Solution:
3.42 ÷ 12 × 3.7
= 1.0545
= 1.055 (4 s. f.)