9.6 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 6:
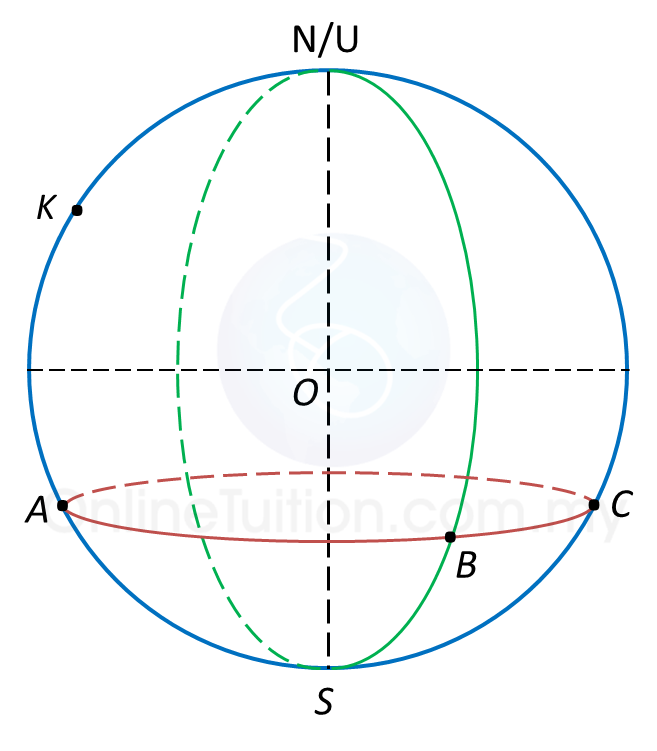
Diagram below shows the locations of points P, Q, R, A, K and C, on the surface of the earth. O is the centre of the earth.

(a) Find the location of A.

(b) Given the distance QR is 3240 nautical miles, find the longitude of Q.

(c) Calculate the distance, in nautical miles of KA, measured along the common parallel latitude.

(d) An aeroplane took off from A and flew due west to K along the common parallel of latitude. Then, it flew due south to Q. The average speed of the aeroplane was 550 knots.
Calculate the total time, in hours, taken for the whole flight.

Solution:

(a)
Longitude of A = (180^o – 15^o) = 165^o E
Latitude of A = 50^o N

Therefore, position of A = (50^o N, 165^o E).

(b)

\begin{array}{l} ∠ Q O R = \frac{3240}{60} \\ = 54^{o} \\ ∴ Longitude of Q = (165^{o} - 54^{o}) E \\ = 111^{o} E \end{array}

(c)
Distance of KA
= 54 x 60 x cos 50^o= 2082.6 nautical miles

(d)

\begin{array}{l} Total distance = A K + K Q \\ = 2082.6 + (50 \times 60) \\ = 5082.6 nautical miles \\ Total time = \frac{5082.6}{550} \\ = 9.241 hours \end{array}

9.6 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 5:
A (53^o N, 84^o E), B (53^o N, 25^o W), C and D are four points on the surface of the earth. AC is the diameter of the parallel of latitude 53^o N.

(a) State the location of C.

(b) Calculate the shortest distance, in nautical mile, from A to C measured along the surface of the earth.

(c) Calculate the distance, in nautical mile, from A due east B measured along the common parallel of latitude.

(d) An aeroplane took off from B and flew due south to D. The average speed of the flight was 420 knots and the time taken was 6½ hours.
Calculate
(i) the distance, in nautical mile, from B to D measured along the meridian.
(ii) the latitude of D.

Solution:

(a)
Latitude of C = 53^o N
Longitude of C = (180^o – 84^o) E = 96^o E
Therefore location of C = (53^o N, 96^o E)

(b)
Shortest distance from A to C
= (180 – 53 – 53) x 60
= 74 x 60
= 4440 nautical miles

(c)
Distance from A to B
= (84 – 25) x 60 x cos 53^o= 59 x 60 x cos 53^o= 2130.43 nautical miles

(d)

\begin{array}{l} (i) \\ Distance travel from B to D \\ = 420 \times 6 \frac{1}{2} \leftarrow \begin{array}{l} Distance travelled \\ = average speed \times time taken \end{array} \\ = 2730 nautical miles \\ (ii) \\ Difference in latitude between B to D \\ = \frac{2730}{60} \\ = {45.5}^{o} \\ ∴ Latitude of D = (53^{o} - {45.5}^{o}) N \\ = {7.5}^{o} N \end{array}

9.6 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 4:
P (25^o N, 35^o E), Q (25^o N, 40^o W), R and S are four points on the surface of the earth. PS is the diameter of the common parallel of latitude 25^o N.

(a) Find the longitude of S.

(b) R lies 3300 nautical miles due south of P measured along the surface of the earth.
Calculate the latitude of R.

(c) Calculate the shortest distance, in nautical mile, from P to S measured along the surface of the earth.

(d) An aeroplane took off from R and flew due north to P. Then, it flew due west to Q.
The total time taken for the whole flight was 12 hours 24 minutes.

(i) Calculate the distance, in nautical mile, from P due west Q measured along the common parallel of latitude.
(ii) Calculate the average speed, in knot, of the whole flight.

Solution:
(a)
Longitude of S = (180^o – 35^o) W = 145^o W

(b)

\begin{array}{l} ∠ P O R = \frac{3300}{60} \\ = 55^{o} \\ Latitude of R = {(55 - 25)}^{o} \\ = 30^{o} S \end{array}

(c)
Shortest distance from P to S
= (65 + 65) x 60
= 130 x 60
= 7800 nautical miles

(d)(i)
Distance of PQ
= (35 + 40) x 60 x cos 25^o= 75 x 60 x cos 25^o= 4078.4 nautical miles

\begin{array}{l} (ii) \\ Total distance travelled \\ R P + P Q \\ = 3300 + 4078.4 \\ = 7378.4 nautical miles \\ Average speed = \frac{Total distance travelled}{Time taken} \\ = \frac{7378.4}{12.4} \leftarrow 12 hours 24 min = 12 + \frac{12}{60} = 12 + 0.4 \\ = 595.0 knot \end{array}

9.6 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 3:
Diagram below shows the locations of points A (34^o S, 40^o W) and B (34^o S, 80^o E) which lie on the surface of the earth. AC is a diameter of the common parallel of latitude 34^o S.

(a) State the longitude of C.

(b) Calculate the distance, in nautical mile, from A due east to B, measured along the common parallel of latitude 34^o S.

(c) K lies due north of A and the shortest distance from A to K measured along the surface of the earth is 4440 nautical miles.
Calculate the latitude of K.

(d) An aeroplane took off from B and flew due west to A along the common parallel of latitude. Then, it flew due north to K. The average speed for the whole flight was 450 knots.
Calculate the total time, in hours, taken for the whole flight.

Solution:
(a)
Longitude of C = (180^o – 40^o) E = 140^o E

(b)
Distance of AB
= (40 + 80) x 60 x cos 34^o= 120 x 60 x cos 34^o= 5969 nautical miles

(c)

\begin{array}{l} ∠ A O K = \frac{4440}{60} \\ = 74^{o} \\ Latitude of K = {(74 - 34)}^{o} N \\ = 40^{o} N \end{array}

(d)

\begin{array}{l} Total distance travelled \\ B A + A K \\ = 5969 + 4440 \\ = 10409 nautical miles \\ Total time taken = \frac{Total distance travelled}{Average speed} \\ = \frac{10409}{450} \\ = 23.13 hours \end{array}

7.5 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 7:
Diagram below shows 4 cards labelled with letters.

Two cards are chosen at random from the box, one by one, without replacement.
(a) List the sample space.
(b) Find the probability that
(i) at least one card chosen is labelled C,
(ii) both cards chosen are labelled with same letter.

Solution:
(a)
Sample space, S
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₁, O₂), (O₁, L), (O₂, C), (O₂, O₁), (O₂, L), (L, C), (L, O₁), (L, O₂)}
n(S) = 12

(b)(i)
At least one card chosen is labelled C
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₂, C), (L, C)}

Probability = \frac{6}{12} = \frac{1}{2}

(b)(ii)
Both cards chosen are labelled with same letter
= {(O₁, O₂), (O₂, O₁)}

Probability = \frac{2}{12} = \frac{1}{6}

Question 8 (6 marks):
A bag contains five cards, labelled with the letters I, J, K, M and U.
One card is picked at random from the bag and the letter is recorded. Without replacement, another card is picked at random from the bag and the letter is also recorded.

(a) Complete the sample space in the answer space.

(b) By listing all the possible outcomes of the event, find the probability that

(i) the first card picked is labelled with a vowel.

(ii) the first card picked is labelled with a consonant and the second card picked is labelled with a vowel.

Answer:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , ), ( , )}

Solution:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}

(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}

\begin{array}{l} Probability of first card with vowels \\ = \frac{8}{20} \\ = \frac{2}{5} \end{array}

(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}

\begin{array}{l} Probability \\ = \frac{6}{20} \\ = \frac{3}{10} \end{array}

7.5 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 5:
A fair dice is tossed. Then a card is picked at random from a box containing a yellow, a red and a purple card.

(a) By using the letter Y to represent the yellow card, the letter R to represent the red card and the letter P to represent the purple card, complete the sample space in the diagram in the answer space.

(b) By listing down all the possible outcomes of the event, find the probability that
(i) a number less than six and a red card are chosen.
(ii) a number greater than three or a purple card is chosen.

Answer:
(a)

Solution:
(a)

(b)

\begin{array}{l} (i) \\ Sample space of a number less than six and a red card are chosen \\ {(1, R), (2, R), (3, R), (4, R), (5, R)} \\ Probability = \frac{5}{18} \\ (ii) \\ Sample space of a number greater than three or a purple card is chosen \\ {(4, Y), (5, Y), (6, Y), (4, R), (5, R), (6, R), (4, P), (5, P), (6, P) \\ , (1, P), (2, P), (3, P)} \\ Probability = \frac{12}{18} \\ = \frac{2}{3} \end{array}

Question 6:
A coin is tossed and a dice is rolled simultaneously. By listing the sample of all the possible outcomes of the event, find the probability that
(a) a head and an odd number are obtained.
(b) a head or a number greater than 4 are obtained.

Solution:

\begin{array}{l} (a) \\ Sample space of a head and an odd number \\ {(H, 1), (H, 3), (H, 5)} \\ Probability = \frac{3}{12} \\ = \frac{1}{4} \\ (b) \\ Sample space of a head or a number greater than 4 \\ {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 5), (T, 6)} \\ Probability = \frac{8}{12} \\ = \frac{2}{3} \end{array}

7.5 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

7.5.2 Probability (II), SPM Practice (Long Questions)

Question 3:

Diagram below shows two cards labelled with letters in box A and three numbered cards in box B.

A card is picked at random from box A and then a card is picked at random from box B.

By listing the sample of all possible outcomes of the event, find the probability that

(a) a card labelled M and a card with an even number are picked,

(b) a card labelled Q or a card with a number which is multiple of 2 are picked.

Solution:

Sample space, S

= {(M, 2), (M, 3), (M, 6), (Q, 2), (Q, 3), (Q, 6)}

n(S) = 6

(a)

{(M, 2), (M, 6)}

P (M and even number) = \frac{2}{6} = \frac{1}{3}

(b)

{(Q, 2), (Q, 3), (Q, 6), (M, 2), (M, 6)}

P (Q or multiple of 2) = \frac{5}{6}

Question 4:

Table below shows the names of participants from two secondary schools attending a public speaking training programme.

	Boys	Girls
School A	Karim	Rosita Sally Linda
School B	Ahmad Billy	Nancy

Two participants are required to give speeches at the end of the programme.

(a) A participant is chosen at random from School A and then another participant is chosen at random also from School A.

(i) List all the possible outcomes of the event in this sample space.

(ii)Hence, find the probability that a boy and a girl are chosen.

(b) A participant is chosen at random from the boys group and then another participant is chosen at random from the girls group.

(i) List all the possible outcomes of the event in this sample space.

(ii)Hence, find the probability that both participants chosen are from School B.

Solution:

(a)(i)

Sample space, S

= {(Karim, Rosita), (Karim, Sally), (Karim, Linda), (Rosita, Sally), (Rosita, Linda), (Sally, Linda)}

n(S) = 6

(a)(ii)

{(Karim, Rosita), (Karim, Sally), (Karim, Linda}

P (a boy and a girl) = \frac{3}{6} = \frac{1}{2}

(b)(i)

Sample space, S

= {(Karim, Rosita), (Karim, Sally), (Karim, Linda), (Karim, Nancy), (Ahmad, Rosita), (Ahmad, Sally), (Ahmad, Linda), (Ahmad, Nancy), (Billy, Rosita), (Billy, Sally), (Billy, Linda), (Billy, Nancy)}

n(S) = 12

(b)(ii)

{(Ahmad, Nancy), (Billy, Nancy)}

P (both participants from School B)

\begin{array}{l} = \frac{2}{12} \\ = \frac{1}{6} \end{array}

7.4 SPM Practice (Short Questions)

Posted on May 28, 2020 by Myhometuition

Question 6:
A box contains 18 black cards and 8 blue cards. Fanny puts another 2 black cards and 4 blue cards inside the box. A card is chosen at random from the box.
What is the probability that a black card is chosen?

Solution:

\begin{array}{l} New total number of cards in the box \\ = (18 + 2) + (8 + 4) \\ = 32 \\ Probability a black card is chosen \\ Probability = \frac{18 + 2}{32} \\ = \frac{20}{32} \\ = \frac{5}{8} \end{array}

Question 7:
A fruits seller wants to check the number of rotten apples in each box. Table below shows the number of rotten apples in each box.

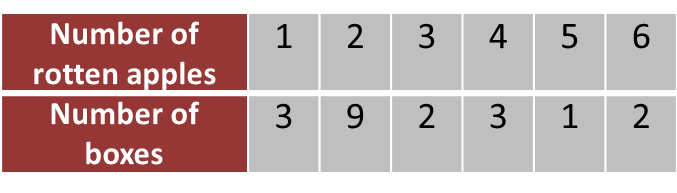Given that there were 55 boxes of apples.
If a box is selected at random, what is the probability that the box does not contain rotten apples?

Solution:

\begin{array}{l} Number of boxes without rotten apples \\ = 55 - (3 + 9 + 2 + 3 + 1 + 2) \\ = 55 - 20 \\ = 35 \\ Probability = \frac{35}{55} = \frac{7}{11} \end{array}

Question 8:
A form 5 science class has 15 boy students and a number of girl students. A student is chosen at random from the class. The probability of choosing a boy student is

\frac{3}{5}

.
Find the number of girl students in the class.

Solution:

\begin{array}{l} Let x be the number of girl students in the class . \\ P (a girl student) = 1 - \frac{3}{5} \\ = \frac{2}{5} \\ \frac{x}{15 + x} = \frac{2}{5} \\ 5 x = 30 + 2 x \\ 3 x = 30 \\ x = 10 \end{array}

7.4 SPM Practice (Short Questions)

Posted on May 28, 2020 by Myhometuition

Question 4:
A box contains 5 red cards, 3 yellow cards and a number of green cards. A card is picked at random from the box. Given that the probability of picking a yellow card is

\frac{1}{6}

, find the probability of picking a card that is not green.

Solution:

\begin{array}{l} P (yellow card) = \frac{n (yellow card)}{n (S)} \\ \frac{1}{6} = \frac{3}{n (S)} \\ n (S) = 3 \times 6 \\ = 18 \\ n (not green card) = 5 + 3 = 8 \\ P (not green card) = \frac{8}{18} \\ = \frac{4}{9} \end{array}

Question 5:
In an office, 300 workers go to work by bus, 60 workers go by car and the rest go by motorcycle. A worker is chosen at random. The probability of choosing a worker who goes to work by bus is ⅔.
Find the probability of choosing a worker who does not go to work by motorcycle.

Solution:

\begin{array}{l} Let y be the number of workers who go to office by motorcycle . \\ P (by bus) = \frac{2}{3} \\ \frac{Number of workers (By bus)}{Total number of workers} = \frac{2}{3} \\ \frac{300}{300 + 60 + y} = \frac{2}{3} \\ 900 = 720 + 2 y \\ 2 y = 180 \\ y = 90 \\ Probability = \frac{300 + 60}{360 + 90} \\ = \frac{360}{450} \\ = \frac{4}{5} \end{array}

6.3 SPM Practice (Long Questions)

Posted on May 28, 2020 by Myhometuition

Question 9:
Diagram below shows the speed-time graph for the movement of an object for a period of 34 seconds.

(a) State the duration of time, in seconds, for which the object moves with uniform speed.
(b) Calculate the rate of change of speed, in ms^-2, of the object for the first 8 seconds.
(c) Calculate the value of u, if the average of speed of the object for the last 26 seconds is 6 ms^-1.

Solution:
(a) Duration of time = 26s – 20s = 6s

\begin{array}{l} (b) \\ Rate of change of speed for the first 8 seconds \\ = \frac{10 - 6}{0 - 8} \\ = - \frac{4}{8} \\ = - \frac{1}{2} {ms}^{- 2} \end{array}

\begin{array}{l} (c) \\ Speed = \frac{Distance}{Time} \\ \frac{(\frac{1}{2} \times 12 \times (6 + u)) + (6 \times u) + (\frac{1}{2} \times 8 \times u)}{26} = 6 \\ 36 + 6 u + 6 u + 4 u = 156 \\ 16 u = 120 \\ u = 7.5 {ms}^{- 1} \end{array}

Question 10 (6 marks):
Diagram 11 shows the speed-time graph for the movement of a particle for a period of t seconds.

Diagram 11

(a) State the uniform speed, in ms^-1, of the particle.

(b) Calculate the rate of change of speed, in ms^-2, of the particle in the first 4 seconds.

(c) Calculate the value of t, if the distance travelled in the first 4 seconds is half of the distance travelled from the 6^thsecond to the t^thsecond.

Solution:
(a)
Uniform speed of the particle = 12 ms^-1(b)

\begin{array}{l} Rate of change of speed of particle \\ = \frac{12}{4} \\ = 3 {ms}^{- 2} \end{array}

(c)

\begin{array}{l} Distance travelled in the first 4 seconds \\ = \frac{1}{2} (\begin{array}{l} Distance travelled from the \\ 6^{th} second to t^{th} second \end{array}) \\ \frac{1}{2} \times 4 \times 12 = \frac{1}{2} [\frac{1}{2} (12 + 20) (t - 6)] \\ 24 = \frac{1}{2} [16 (t - 6)] \\ 24 = 8 (t - 6) \\ 24 = 8 t - 48 \\ 3 = t - 6 \\ t = 9 \end{array}