Home › Archive for SPM Maths › Page 9

SPM Maths

4.3 Operations on Statements (Sample Questions 2)

Posted on by

Example 3:
Determine whether each of the following statements is true or false.
(a) 3 × (-4) = -12 and 13 + 6 = 19
(b) 100 × 0.7 = 70 and 12 + (-30) = 18

Solution:
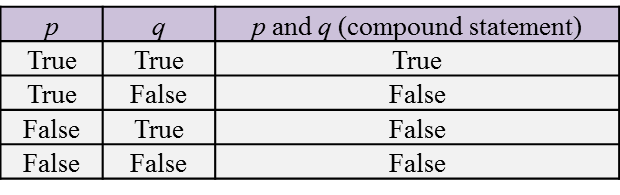
When two statements are combined using ‘and’, a true compound statement is obtained only if both statements are true.
If one or both statements are false, then the compound statement is false.

(a) Both the statements ‘3 × (-4) = -12’ and ‘13 + 6 = 19’ are true. Therefore, the statement ‘3 × (-4) = -12 and 13 + 6 = 19’ is true.

(b) The statement ‘12 + (-30) = 18’ is false. Therefore, the statement ‘100 × 0.7 = 70 and 12 + (-30) = 18’ is false.



Example 4:
Determine whether each of the following statements is true or false.
(a) m + m = m2 or p × p × p = p-3
(b)  64 3 =−4 or  −27 3 =−3

Solution:
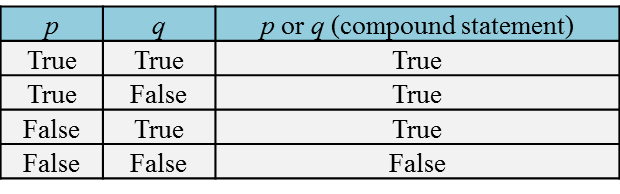
When two statements are combined using ‘or’, a false compound statement is obtained only if both statements are false.
If one or both statements are true, then the compound statement is true.

(a) Both the statements ‘m+ m = m2’ and ‘p × p × p= p-3’ are false. Therefore the statement m + m = m2 or p × p × p = p-3 is false.

(b) The statement  ' − 27 3 = − 3 '  is true. Therefore, the statement  64 3 =−4 or  −27 3 =−3  is true.

4.3 Operations on Statements

Posted on by
4.3 Operations on Statements (Part 3)

(C) Truth Values of Compound Statements using ‘Or’
 
1. When two statements are combined using ‘or’, a false compound statement is obtained only if both statements are false.
 
2. f one or both statements are true, then the compound statement is true.
 
The truth table:
Let p = statement 1 and q= statement 2.
The truth values for ‘p’ or ‘q’ are as follows:


 
Example 6:
Determine the truth value of the following statements.
(a) 60 is divisible by 4 or 9.
(b) 53 = 25 or 43 = 64.
(c) 5 + 7 > 14 or √9 = 2.
 
Solution:
(a)
60 is divisible by 4  ← (p is true)
60 is divisible by 9  ← (q is false)
Therefore, 60 is divisible by 4 or 9 is a true statement. (‘p or q’ is true)
 
(b)
53 = 25  ← (p is false)
43 = 64  ← (q is true)
Therefore, 53 = 25 or 43 = 64 is a true statement. (‘p or q’ is true)
 
(c)
5 + 7 > 14  ← (p is false)
√9 = 2  ← (q is false)
Therefore, 5 + 7 > 14 or √9 = 2 is a false statement. (‘p or q’ is false)

4.3 Operations on Statements

Posted on by
4.3 Operations on Statements (Part 2)
(B) Truth Values of Compound Statements using ‘And’
 
4. When two statements are combined using ‘and’, a true compound statement is obtained only if both statements are true.
 
5. If one or both statements are false, then the compound statement is false.
 
The truth table:
Let p = statement 1 and q = statement 2.
The truth values for ‘p’ and ‘q’ are as follows:

 
Example 5:
Determine the truth value of the following statements.
(a) 12 × (–3) = –36 and 15 – 7 = 8.
(b) 5 > 3 and –4 < –5.
(c) Hexagons have 5 sides and each of the interior angles is 90o.
 
Solution:
(a)
12 × (–3) = –36 ← (p is true)
15 – 7 = 8 ← (q is true)
Therefore 12 × (–3) = –36 and 15 – 7 = 8 is a true statement. (‘p and q’ is true)
 
(b)
5 > 3 ← (p is true)
–4 < –5 ← (q is false)
Therefore 5 > 3 and –4 < –5 is a false statement. (‘p and q’ is false)

(c)
Hexagons have 5 sides. ← (p is false)
Each of the interior angles of Hexagon is 90o. ← (q is false)
Therefore Hexagons have 5 sides and each of the interior angles is 90o is a false statement. (‘p and q’ is false)

3.4 SPM Practice (Long Questions)

Posted on by

Question 7:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R .
On the diagrams in the answer space, shade set
(a) P ∩ Q,
(b) P ' ∩Q∪R


Solution:
(a) 
P ∩ Q


(b) 
P ' ∩Q∪R



Question 8:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R .
On the diagrams in the answer space, shade set
(a) Q ' ∩R
(b) ( Q∪R )∩ P '



Solution:
(a) 
Q ' ∩R


(b) 
( Q∪R )∩ P '



3.4 SPM Practice (Long Questions)

Posted on by

Question 5:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R
On the diagrams in the answer space, shade
(a) P ∩ Q,
(b) Q∩( P ' ∪R).

Solution:
(a) 
P ∩ Q

(b)
Q∩( P ' ∪R).




Question 6:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ=P∪Q∪R
On the diagrams in the answer space, shade
(a) P ∩ Q,
(b) P∩ (Q∪R) ' .

Solution:
(a)
P ∩ Q


(b)
P∩ (Q∪R) ' .



3.4 SPM Practice (Long Questions)

Posted on by

Question 1:
The Venn diagrams in the answer space shows sets X, Y and Z such that the universal set, ξ = X ∪ Y ∪ Z
On the diagrams in the answer space, shade
( a ) X' ∩ Y , ( b ) ( X ∪ Y' ) ∩ Z


Solution:
(a) 
• X’ ∩ Y means the intersection of the region outside X with the region Y.

 
 
(b)
• Find the region of (X υ Y’) first.
• (X υ Y’) means the union of the region X and the region outside Y.
• The region then intersects with region Z to give the result of (X υ Y’) ∩ Z.





Question 2:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ = P υ Q υ R
On the diagrams in the answer space, shade
(a) Q ∩ R,
(b) (P’ ∩ R) υ Q.

Solution:
(a) 
• Q ∩ R means the intersection of the region Q and the region R.



(b)
• Find the region of (P’ ∩ R) first.
• (P’ ∩ R) means the region that is outside P and is inside R.
• The union of this region with region Q give the result of (P’ ∩ R) υ Q.



3.4.2 Sets, SPM Paper 1 (Short Questions 5 – 7)

Posted on by

3.4.2 Sets, SPM Practice Paper 1 (Short Questions)

Question 5:
Diagram below shows a Venn diagram with the number of elements of set P, set Q and set R.

It is given that the universal set, ξ=P∪Q∪R and n( Q' )=n( Q∩R ).
Find the value of x.

Solution:
n(Q)’ = n(Q ∩ R)
3 + 8 + 5 = x– 3 + 9
16 = x + 6
x = 10


Question 6:
Diagram below is a Venn diagram showing the number of quiz participants in set P, set Q and set R.
It is given that the universal set, ξ = P ∪ Q ∪ R , set P = {Science quiz participants}, set Q = {Mathematics quiz participants} and set R = {History quiz participants}.

If the number of participants who participate in only one quiz is 76, find the total number of the participants.

Solution:
Number of participants who participate in only one quiz = 76
(5x – 2) + (x + 6) + (2x + 8) = 76
8x + 12 = 76
8x = 64
x = 8
Total number of the participants
= 76 + 7 + 4 + 5 + 3(8)
= 116


Question 7:
Diagram below is a Venn diagram showing the number of students in set K, set L and set M.
It is given that the universal set, ξ = K ∪ L ∪ M , set K = {Karate Club}, set L = {Life Guards Club} and set M = {Martial Arts Club}.

If the number of students who join both the Life Guards Club and the Martial Arts Club is 8, find the number of students who join only two clubs.

Solution:
Number of students who join both the Life Guards Club and the Martial Arts Club = n(L ∩ M) = 2 + 2x
2 + 2x = 8
2x = 6
x = 3
Number of students who join only two clubs
= x + 4 + 2x
= 3 + 4 + 2(3)
= 13

3.4.1 Sets, SPM Paper 1 (Short Questions 1 – 4)

Posted on by

Question 1:
List all the subsets of set P = {r, s}.
 
Solution:
There are 2 elements, so the number of subsets of set P is 2n = 22= 4.
Set P = {r, s}
Therefore subsets of set P = {r}, {s}, {r, s}, { }.


Question 2:
 
Diagram above shows a Venn diagram with the universal set, ξ = Q υ P.
List all the subset of set P.
 
Solution:
Set P has 3 elements, so the number of subsets of set P is 2n = 23 = 8.
Set P = {2, 3, 5}
Therefore subsets of set P = { }, {2}, {3}, {5}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}.


Question 3:
It is given that the universal set, ξ = {x: 30 ≤ x < 42, x is an integer} and set P = {x: x is a number such that the sum of it its two digits is an even number}.
Find set P’.
 
Solution:
ξ = {30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41}
P = {31, 33, 35, 37, 39, 40}
Therefore P’ = {30, 32, 34, 36, 38, 41}.


Question 4:
Given that universal set ξ = {x : 3 < x ≤ 16, x  is an integer},
Set A = {4, 11, 13, 16},
Set B = {x : x is an odd number} and
Set C = {x : x is a multiple of 3}.

The elements of the set (A υ C)’ ∩ B are

Solution:
ξ = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
A = {4, 11, 13, 16}
B = {5, 7, 9, 11, 13, 15}
C = {6, 9, 12, 15}
(A υ C)’ = {5, 7, 8, 10, 14}
Therefore (A υ C)’ ∩ B = {5, 7}.

3.3 Operations on Sets

Posted on by
3.3b Union of Sets (Part 2)
Example 1:
The Venn diagram below shows the number of elements in the universal set, ξ, set P, set Q and R.


Given n(Q) = n(P υ R)’, find n(ξ).
 
Solution:
n(Q) = n (P υ R)’
2x + 6 + 1 + 5 = 2x + 2x
2x + 12 = 4x
2x = 12
x = 6
 
n(ξ) = 2x + 2x + x + 7 + 6 + 1 + 5
= 5x+ 19
= 5(6) + 19
= 30 + 19
= 49
 


Example 2:
Diagram below is a Venn diagram showing the universal set, ξ = {Form 3 students}, set A = {Students who play piano} and set B = {Students who play violin}.
 

 
Given n(ξ) = 60, n(A) = 25, n(B) = 12 and n(A ∩ B) = 8, find the number of students who do not play the two instruments.

Solution:
The students who do not play the two instruments are represented by the shaded region, (A υ B)’.

 
Number of students who do not play the two instruments
= n (A υ B)’
= 60 – 17 – 8 – 4
= 31
 

3.3a Intersection of Sets (Part 2)

Posted on by
3.3a Intersection of Sets
Example 1:
Given that A= {3, 4, 5, 6, 7}, B = {4, 5, 7, 8, 9, 12} and C = {3, 5, 7, 8, 9, 10}.
(a) Find A∩B∩C.
(b) Draw a Venn diagram to represent A∩B∩C.
 
Solution:
(a)  A∩B∩C= {5, 7}

(b)


 

4. The complement of the intersection of two sets, P and Q, represented by (P ∩ Q)’, is a set that consists of all the elements of the universal set, ξ, but not the elements of P ∩ Q.

5. The complement of set (P ∩ Q)’ is represented by the shaded region as shown in the Venn diagram.