Question 10 (5 marks):
The table below shows some members of Red Crescent Society and St John Ambulance Society that are instructed to do an outdoor tasks at various places during the Flag Day.


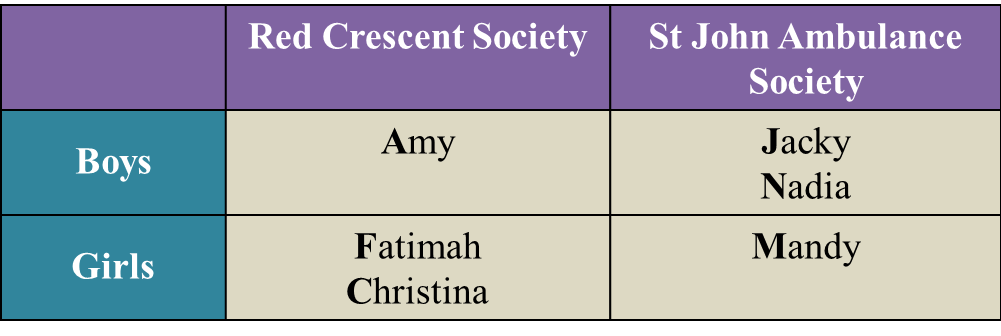
Two members from the societies were dropped off random at those places.
(a) List all the possible outcomes of the event in this sample space.
You also may use the letters such as A for Amy and so on.

(b) By listing down all the possible outcomes of the event, find the probability that
(i) a boy and a girl were dropped off at a certain place.
(ii) both members that were dropped off at a certain place are from the same society.


Solution:
(a)
S = {(A, J), (A, N), (A, F), (A, C), (A, M), (J, A), (J, N), (J, F), (J, C), (J, M), (N, A), (N, J), (N, F), (N, C), (N, M), (F, A), (F, J), (F, N), (F, C), (F, M), (C, A), (C, J), (C, N), (C, F), (C, M),(M, A), (M, J), (M, N), (M, F), (M, C)}

(b)(i)
{(A, F), (A, C), (A, M), (J, F), (J, C), (J, M), (N, F), (N, C), (N, M), (F, A), (F, J), (F, N), (C, A), (C, J), (C, N), (M, A), (M, J), (M, N)}
$\begin{array}{l}\text{Probability}\\ =\frac{18}{30}\\ =\frac{3}{5}\end{array}$

(b)(ii)
{(A, F), (A, C), (F, A), (F, C), (C, A), (C, F), (J, N), (J, M), (N, J), (N, M), (M, J), (M, N)}
$\begin{array}{l}\text{Probability}\\ =\frac{12}{30}\\ =\frac{2}{5}\end{array}$

Question 9 (6 marks):
Diagram 10.1 shows a disc with four equal sectors and a fixed pointer. Each sector is labelled with water heater, oven, television and iron respectively. Diagram 10.2 shows a box which contains three cash vouchers, RM10, RM20 and RM50.



A lucky customer in a supermarket is given a chance to spin the disc once and then draw a cash voucher from the box.
(a) List the sample space for the combination of prizes that can be won.

(b) By listing down all the possible outcomes of the event, find the probability that

(i) the customer wins a television or cash voucher worth RM50,

(ii) the customer does not wins the water heater and the cash voucher worth RM20.


Solution:
(a)
S = {(Water heater, RM10), (Water heater, RM20), (Water heater, RM50), (Oven, RM10), (Oven, RM20), (Oven, RM50), (Television, RM10), (Television, RM20), (Television, RM50), (Iron, RM10), (Iron, RM20), (Iron, RM50)}

(b)(i)
{( Water heater, RM50), (Oven, RM50), (Iron, RM50), (Television, RM10), (Television, RM20), (Television, RM50)}
$\begin{array}{l}\text{Probability}\\ =\frac{6}{12}\\ =\frac{1}{2}\end{array}$

(b)(ii)
$\begin{array}{l}\text{Probability}\\ =1-P\left(\text{Water heater, RM20}\right)\\ =1-\frac{1}{12}\\ =\frac{11}{12}\end{array}$

Question 7:
Diagram below shows 4 cards labelled with letters.


Two cards are chosen at random from the box, one by one, without replacement.
(a) List the sample space.
(b) Find the probability that
(i) at least one card chosen is labelled C,
(ii) both cards chosen are labelled with same letter.

Solution:
(a)
Sample space, S
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₁, O₂), (O₁, L), (O₂, C), (O₂, O₁), (O₂, L), (L, C), (L, O₁), (L, O₂)}
n(S) = 12

(b)(i)
At least one card chosen is labelled C
= {(C, O₁), (C, O₂), (C, L), (O₁, C), (O₂, C), (L, C)}
$\text{Probability}=\frac{6}{12}=\frac{1}{2}$

(b)(ii)
Both cards chosen are labelled with same letter
= {(O₁, O₂), (O₂, O₁)}
$\text{Probability}=\frac{2}{12}=\frac{1}{6}$

Question 8 (6 marks):
A bag contains five cards, labelled with the letters I, J, K, M and U.
One card is picked at random from the bag and the letter is recorded. Without replacement, another card is picked at random from the bag and the letter is also recorded.

(a) Complete the sample space in the answer space.

(b) By listing all the possible outcomes of the event, find the probability that

(i) the first card picked is labelled with a vowel.

(ii) the first card picked is labelled with a consonant and the second card picked is labelled with a vowel.

Answer:
{(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (   , ), (   , ), ( , ), ( , ), (   , ), (   ,   ), (   , ), (   ,   ), (   , ), (   ,   )}


Solution:
(a)
S = {(I, J), (I, K), (I, M), (I, U), (J, I), (J, K), (J, M), (J, U), (K, I), (K, J), (K, M), (K, U), (M, I), (M, J), (M, K), (M, U), (U, I), (U, J), (U, K), (U, M)}

(b)(i)
{(I, J), (I, K), (I, M), (I, U), (U, I), (U, J), (U, K), (U, M)}
$\begin{array}{l}\text{Probability of first card with vowels}\\ =\frac{8}{20}\\ =\frac{2}{5}\end{array}$

(b)(ii)
{(J, I), (J, U), (K, I), (K, U), (M, I), (M, U)}
$\begin{array}{l}\text{Probability}\\ =\frac{6}{20}\\ =\frac{3}{10}\end{array}$

Question 5:
A fair dice is tossed. Then a card is picked at random from a box containing a yellow, a red and a purple card.

(a) By using the letter Y to represent the yellow card, the letter R to represent the red card and the letter P to represent the purple card, complete the sample space in the diagram in the answer space.

(b) By listing down all the possible outcomes of the event, find the probability that
(i) a number less than six and a red card are chosen.
(ii) a number greater than three or a purple card is chosen.

Answer:
(a)

Solution:
(a)

(b)
$\begin{array}{l}\left(\text{i}\right)\\ \text{Sample space of a number less than six and a red card are chosen}\\ \left\{\left(1,R\right),\left(2,R\right),\left(3,R\right),\left(4,R\right),\left(5,R\right)\right\}\\ \text{Probability}=\frac{5}{18}\\ \\ \left(\text{ii}\right)\\ \text{Sample space of a number greater than three or a purple card is chosen}\\ \{\left(4,Y\right),\left(5,Y\right),\left(6,Y\right),\left(4,R\right),\left(5,R\right),\left(6,R\right),\left(4,P\right),\left(5,P\right),\left(6,P\right)\\ ,\left(1,P\right),\left(2,P\right),\left(3,P\right)\}\\ \text{Probability}=\frac{12}{18}\\ =\frac{2}{3}\end{array}$

Question 6:
A coin is tossed and a dice is rolled simultaneously. By listing the sample of all the possible outcomes of the event, find the probability that
(a) a head and an odd number are obtained.
(b) a head or a number greater than 4 are obtained.

Solution:
$\begin{array}{l}\left(a\right)\\ \text{Sample space of a head and an odd number}\\ \left\{\left(H,1\right),\left(H,3\right),\left(H,5\right)\right\}\\ \text{Probability}=\frac{3}{12}\\ =\frac{1}{4}\\ \\ \left(b\right)\\ \text{Sample space of a head or a number greater than 4}\\ \left\{\left(H,1\right),\left(H,2\right),\left(H,3\right),\left(H,4\right),\left(H,5\right),\left(H,6\right),\left(T,5\right),\left(T,6\right)\right\}\\ \text{Probability}=\frac{8}{12}\\ =\frac{2}{3}\end{array}$

{(Q, 2), (Q, 3), (Q, 6), (M, 2), (M, 6)}

	Boys	Girls
School A	Karim	Rosita Sally Linda
School B	Ahmad Billy	Nancy

$\begin{array}{l}=\frac{2}{12}\\ =\frac{1}{6}\end{array}$

Question 6:
A box contains 18 black cards and 8 blue cards. Fanny puts another 2 black cards and 4 blue cards inside the box. A card is chosen at random from the box.
What is the probability that a black card is chosen?

Solution:
$\begin{array}{l}\text{New total number of cards in the box}\\ =\left(18+2\right)+\left(8+4\right)\\ =32\\ \\ \text{Probability a black card is chosen}\\ \text{Probability}=\frac{18+2}{32}\\ =\frac{20}{32}\\ =\frac{5}{8}\end{array}$

Question 7:
A fruits seller wants to check the number of rotten apples in each box. Table below shows the number of rotten apples in each box.
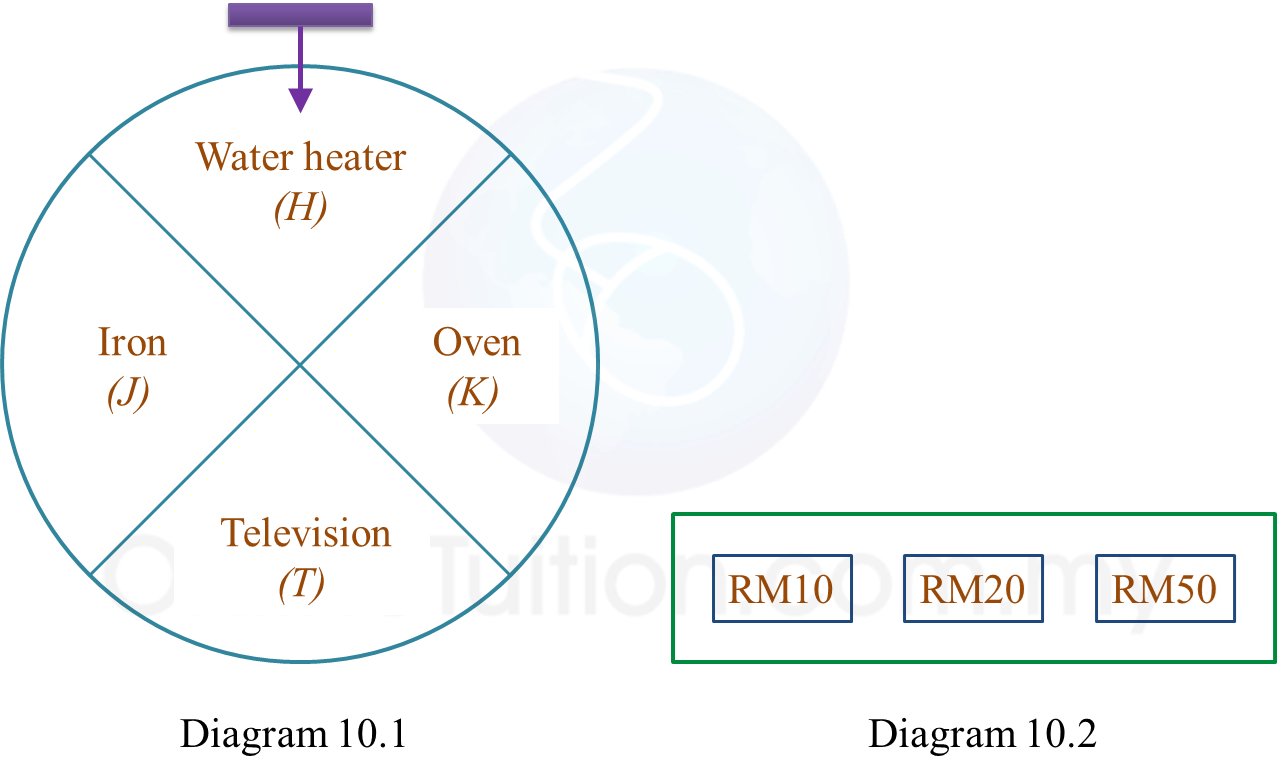
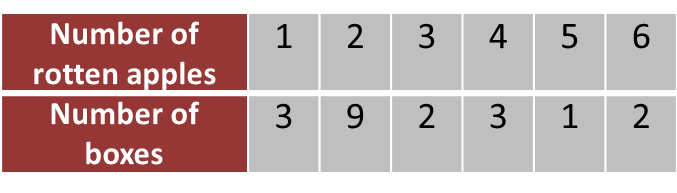Given that there were 55 boxes of apples.
If a box is selected at random, what is the probability that the box does not contain rotten apples?

Solution:
$\begin{array}{l}\text{Number of boxes without rotten apples}\\ =55-\left(3+9+2+3+1+2\right)\\ =55-20\\ =35\\ \\ \text{Probability}=\frac{35}{55}=\frac{7}{11}\end{array}$

Question 8:
A form 5 science class has 15 boy students and a number of girl students. A student is chosen at random from the class. The probability of choosing a boy student is $\frac{3}{5}$ .
Find the number of girl students in the class.

Solution:
$\begin{array}{l}\text{Let }x\text{ be the number of girl students in the class}\text{.}\\ \text{P}\left(\text{a girl student}\right)=1-\frac{3}{5}\\ =\frac{2}{5}\\ \frac{x}{15+x}=\frac{2}{5}\\ 5x=30+2x\\ 3x=30\\ x=10\end{array}$

Question 4:
A box contains 5 red cards, 3 yellow cards and a number of green cards. A card is picked at random from the box. Given that the probability of picking a yellow card is $\frac{1}{6}$ , find the probability of picking a card that is not green.

Solution:
$\begin{array}{l}\text{P}\left(\text{yellow card}\right)=\frac{n\left(\text{yellow card}\right)}{n\left(S\right)}\\ \frac{1}{6}=\frac{3}{n\left(S\right)}\\ n\left(S\right)=3\times 6\\ =18\\ \\ n\left(\text{not green card}\right)=5+3=8\\ \text{P}\left(\text{not green card}\right)=\frac{8}{18}\\ =\frac{4}{9}\end{array}$

Question 5:
In an office, 300 workers go to work by bus, 60 workers go by car and the rest go by motorcycle. A worker is chosen at random. The probability of choosing a worker who goes to work by bus is ⅔.
Find the probability of choosing a worker who does not go to work by motorcycle.

Solution:
$\begin{array}{l}\text{Let }y\text{ be the number of workers who go to office by motorcycle}\text{.}\\ \text{P}\left(\text{by bus}\right)=\frac{2}{3}\\ \frac{\text{Number of workers }\left(\text{By bus}\right)}{\text{Total number of workers}}=\frac{2}{3}\\ \frac{300}{300+60+y}=\frac{2}{3}\\ 900=720+2y\\ 2y=180\\ y=90\\ \\ \text{Probability}=\frac{300+60}{360+90}\\ =\frac{360}{450}\\ =\frac{4}{5}\end{array}$