Quadratic Equations Long Questions (Question 14 & 15)

Posted on May 29, 2020 by Myhometuition

Question 14 (4 marks):
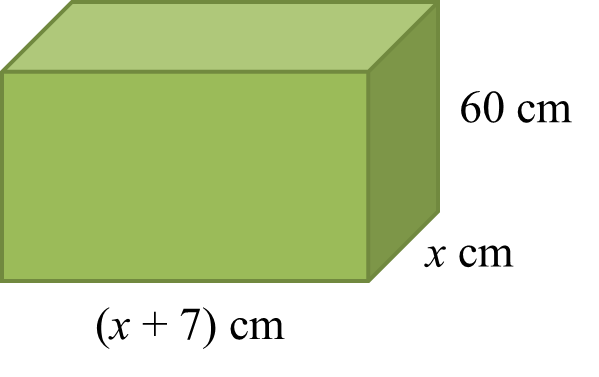
An aquarium has the length of (x + 7) cm, the width of x cm and the height of 60 cm.
The total volume of the aquarium is 48000 cm³. The aquarium will be filled fully with water.
Calculate the value of x.

Solution:

\begin{array}{l} Volume of aquarium = 48000 {cm}^{3} \\ So, \\ (x) (x + 7) (60) {cm}^{3} = 48000 {cm}^{3} \\ (x) (x + 7) = \frac{48000}{60} \\ x^{2} + 7 x = 800 \\ x^{2} + 7 x - 800 = 0 \\ (x - 25) (x + 32) = 0 \\ x - 25 = 0 or x + 32 = 0 \\ x = 25 or x = - 32 (not accepted) \\ So the value of x = 25 cm \end{array}

Question 15 (4 marks):
Diagram 3 shows a garden path with a rectangular shape. There are 8 similar circular stepping stone built in the path.

Given the area of the path is 32 m², find the diameter, in m, of one piece of stepping stone.

Solution:

\begin{array}{l} Given the area of the path \\ = 32 m^{2} = 320000 {cm}^{2} \\ x (x + 4) = 320000 \\ x^{2} + 4 x - 320000 = 0 \\ a = 1, b = 4, c = - 320000 \\ x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ x = \frac{- 4 \pm \sqrt{4^{2} - 4 (1) (- 320000)}}{2 (1)} \\ x = \frac{- 4 \pm \sqrt{1280016}}{2} \\ x = \frac{- 4 + 1131.38}{2} or \frac{- 4 - 1131.38}{2} \\ x = 563.69 or - 567.69 (ignored) \\ Diameter of one piece of stepping \\ stone = x \\ = 563.69 cm \\ = 5.64 m \end{array}

2.3 Quadratic Equations

Posted on April 23, 2020 by user

2.3 Quadratic Equations

1. Quadratic equations are equations which fulfil the following characteristics:

(a) Have an equal ‘=’ sign

(b) Contain only one unknown

(c) Highest power of the unknown is 2.

For example,

2. The general form of a quadratic equation is written as:

(a)
ax² + bx + c = 0,

where a ≠ 0, b ≠ 0 and c ≠ 0,

example: 4x²+ 13x – 12 = 0

(b)
ax² + bx = 0,

where a ≠ 0, b ≠ 0 but c = 0,

example: 7x²+ 9x = 0

where a ≠ 0, c ≠ 0 but b = 0,

example: 9x²– 3 = 0

Example 1:

Write each quadratic equation in the general form.

(a) x² – 5x = 12

(b) -2 + 5x²– 6x = 0

(d) (x – 2)(x + 6) = 0

(e) 3 – 13x = 4 (x² + 2)

(f)

2 - y = \frac{1 - 3 y}{y}

(g)

\frac{p}{4} = \frac{2 p^{2} - 3}{10}

(h)

\frac{y^{2} + 5}{4} = \frac{y - 1}{2}

(i)

\frac{4 p}{7} = p (7 p - 6)

Solution:

A quadratic equation in the general form is written as ax² + bx + c = 0

(a) x² – 5x = 12

x² – 5x -12 = 0

(b) –2 + 5x²– 6x = 0

5x² – 6x –2 = 0

(c) 7p² – 3p = 4p²+ 4p – 3

7p² – 3p – 4p²– 4p + 3 = 0

3p² – 7p + 3 = 0

(d) (x – 2)(x + 6) = 0

x² + 6x – 2x– 12 = 0

x² + 4x – 12 = 0

(e) 3 – 13x = 4 (x² + 2)

3 – 13x = 4x² + 8

–4x²– 8 + 3 – 13x = 0

–4x² – 13x – 5 = 0

4x² + 13x + 5 = 0

(f)

2 - y = \frac{1 - 3 y}{y}

2y – y²= 1 – 3y

2y – y²– 1 + 3y = 0

– y²+ 5y – 1 = 0

y² – 5y + 1 = 0

(g)

\frac{p}{4} = \frac{2 p^{2} - 3}{10}

10p = 8p² – 12

–8p² + 10p +12 = 0

8p² – 10p – 12 = 0

(h)

\frac{y^{2} + 5}{4} = \frac{y - 1}{2}

2y² + 10 = 4y – 4

2y² – 4y + 10 + 4 = 0
2y² – 4y + 14 = 0

(i)

\frac{4 p}{7} = p (7 p - 6)

4p = 7p (7p– 6)

4p = 49p² – 42p

– 49p² + 42p + 4p = 0

49p² – 46p = 0

Quadratic Equations Long Questions (Question 5 – 7)

Posted on April 23, 2020 by user

Question 5:

Solve the equation:

(m + 2)(m – 4) = 7(m – 4).

Solution:

(m + 2)(m – 4) = 7(m – 4)

m²– 4m + 2m – 8 = 7m – 28

m²– 9m + 20 = 0

(m – 5)(m – 4) = 0

m = 5 or m = 4

Question 6:

Solve the equation:

\frac{- 6 y - 2}{y} = \frac{7}{1 - y}

Solution:

\begin{array}{l} \frac{- 6 y - 2}{y} = \frac{7}{1 - y} \\ (- 6 y - 2) (1 - y) = 7 y \\ - 6 y + 6 y^{2} - 2 + 2 y - 7 y = 0 \\ 6 y^{2} - 11 y - 2 = 0 \\ (6 y + 1) (y - 2) = 0 \\ 6 y + 1 = 0 or y = 2 \\ y = - \frac{1}{6} \end{array}

Question 7:

Solve the equation:

\frac{4 m}{7} = m (8 m - 9)

Solution:

\begin{array}{l} \frac{4 m}{7} = m (8 m - 9) \\ 4 m = 7 m (8 m - 9) \\ 4 m = 56 m^{2} - 63 m \\ 56 m^{2} - 63 m - 4 m = 0 \\ 56 m^{2} - 67 m = 0 \\ m (56 m - 67) = 0 \\ m = 0 or 56 m - 67 = 0 \\ m = \frac{67}{56} \end{array}

2.4 Roots of Quadratic Equations

Posted on April 23, 2020 by user

2.4 Roots of Quadratic Equations

1. A root of quadratic equation is the value of the unknown which satisfies the quadratic equation.

2. Roots of an equation are also called the solution of an equation.

3. To solve a quadratic equation by the factorisation method, follow the steps below:

Step 1: Express the quadratic equation in general form ax² + bx + c = 0.

Step 2: Factorise the quadratic expression ax² + bx + c = 0 as the product of two linear expressions, that is, (mx+ p) (nx + q) = 0.

Step 3: Equate each factor to zero and obtain the roots or solutions of the quadratic equation.

\begin{array}{l} m x + p = 0 or n x + q = 0 \\ x = - \frac{p}{m} or x = - \frac{q}{n} \end{array}

Example 1:

Solve the quadratic equation

\frac{2 x^{2} - 5}{3} = 3 x

Solution:

\frac{2 x^{2} - 5}{3} = 3 x

2x² – 5 = 9x

2x² – 9x – 5 = 0

(x – 5)(2x + 1) = 0

x – 5 = 0, x = 5

or 2x + 1 = 0

x = - \frac{1}{2}

Therefore, x = 5 and x = ½ are roots or solutions of the quadratic equation.

Example 2:

Solve the quadratic equation 4x² – 12 = –13x

Solution:

4x² – 12 = –13x

4x² + 13x – 12 = 0

(4x – 3)(x + 4) = 0

4x – 3 = 0,

x = \frac{3}{4}

or x + 4 = 0

x = –4

Example 3:

Solve the quadratic equation 5x² = 3 (x + 2) – 4

Solution:

5x² = 3 (x + 2) – 4

5x² = 3x + 6 – 4

5x² – 3x – 2 = 0

(5x + 2)(x – 1) = 0

5x + 2 = 0,

x = - \frac{2}{5}

or x – 1 = 0

x = 1

Example 4:

Solve the quadratic equation

\frac{3 x (x - 3)}{4} = - x + 3.

Solution:

\frac{3 x (x - 3)}{4} = - x + 3

3x² – 9x = – 4x + 12

3x² – 5x – 12 = 0

(3x + 4)(x – 3) = 0

3x + 4 = 0,

x = - \frac{4}{3}

or x – 3 = 0

x = 3

2.1 Quadratic Expression (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Form a quadratic expression by multiplying each of the following.

(a) (6p – 2)(2p – 1)

(b) (m + 5)(4 – 7m)

Solution:

(a) (6p – 2)(2p – 1)

= (6p)(2p) + (6p)(-1) + (-2)(2p) +(-2)(-1)

= 12p² – 6p – 4p + 2

= 12p² – 10p + 2

(b) (m + 5)(4 – 7m)

= (m)(4) + (m)(-7m) + (5)(4) + (5)(-7m)

= 4m – 7m² + 20 – 35m

= – 7m² – 31m+ 20

= (x)(2x) + (x)(-3) + (2)(2x) + (2)(-3)

= 2x²-3x + 4x – 6

= 2x² + x - 6

Quadratic Equations Long Questions (Question 8 – 10)

Posted on April 23, 2020 by user

Question 8:
Solve the following quadratic equation:
4x (x + 4) = 9 + 16x

Solution:

\begin{array}{l} 4 x (x + 4) = 9 + 16 x \\ 4 x^{2} + 16 x = 9 + 16 x \\ 4 x^{2} - 9 = 0 \\ {(2 x)}^{2} - 3^{2} = 0 \\ (2 x + 3) (2 x - 3) = 0 \\ 2 x + 3 = 0 or 2 x - 3 = 0 \\ 2 x = - 3 2 x = 3 \\ x = - \frac{3}{2} x = \frac{3}{2} \end{array}

Question 9:
Solve the following quadratic equation:
(x + 2)² = 2x + 7

Solution:

\begin{array}{l} {(x + 2)}^{2} = 2 x + 7 \\ x^{2} + 4 x + 4 = 2 x + 7 \\ x^{2} - 2 x - 3 = 0 \\ (x + 1) (x - 3) = 0 \\ x + 1 = 0 or x - 3 = 0 \\ x = - 1 x = 3 \end{array}

Question 10:
Solve the following quadratic equation:

- \frac{2}{3 x - 5} = \frac{x}{3 x - 1}

Solution:

\begin{array}{l} - \frac{2}{3 x - 5} = \frac{x}{3 x - 1} \\ - 2 (3 x - 1) = x (3 x - 5) \\ - 6 x + 2 = 3 x^{2} - 5 x \\ 3 x^{2} - 5 x + 6 x - 2 = 0 \\ 3 x^{2} + x - 2 = 0 \\ (3 x - 2) (x + 1) = 0 \\ 3 x - 2 = 0 or x + 1 = 0 \\ 3 x = 2 x = - 1 \\ x = \frac{2}{3} x = - 1 \end{array}

2.2 Factorisation of Quadratic Expression

Posted on April 23, 2020 by user

2.2 Factorisation of Quadratic Expression

(A) Factorisation quadratic expressions of the form ax² + bx + c, b = 0 or c = 0

1. Factorisation of quadratic expressions is a process of finding two linear expressions whose product is the same as the quadratic expression.

2. Quadratic expressions ax² + c and ax² + bx that consist of two terms can be factorised by finding the common factors for both terms.

Example 1:

Factorise each of the following:

(a) 2x²+ 6

(b) 7p²– 3p

(c) 6x²– 9x

Solution:

(a) 2x²+ 6 = 2 (x² + 3) ← (2 is common factor)

(b) 7p²– 3p = p (7p – 3) ← (p is common factor)

(c) 6x²– 9x = 3x (2x – 3) ← (3x is common factor)

(B) Factorisation of quadratic expressions in the form ax² – c , where a and c are perfect squares

Example 2:

(a) 9p²– 16

(b) 25x²– 1

(c)

\frac{1}{4} - \frac{1}{25} x^{2}

Solution:

(a) 9p²– 16 = (3p)² – 4²= (3p – 4) (3p + 4)

(b) 25x²– 1 = (5x)² – 1²= (5x – 1) (5x + 1)

(c)

\begin{array}{l} \frac{1}{4} - \frac{1}{25} x^{2} = {(\frac{1}{2})}^{2} - {(\frac{1}{5} x)}^{2} \\ = (\frac{1}{2} - \frac{1}{5} x) (\frac{1}{2} + \frac{1}{5} x) \end{array}

(C) Factorisation quadratic expressions in the form ax² + bx + c, where a ≠ 0, b ≠ 0 and c ≠ 0

Example 3:

Factorise each of the following

(a) 3y²+ 2y – 8

(b) 4x²– 12x + 9

Solution:

(a)

Factorise using the Cross Method

3y²+ 2y – 8 = (3y – 4) (y + 2)

(b)

4x²– 12x + 9 = (2x – 3) (2x – 3)

2.1 Quadratic Expression

Posted on April 23, 2020 by user

(A) Identifying quadratic expression

1. A quadratic expression is an algebraic expression of the form ax² + bx + c, where a, b and c are constants, a ≠ 0 and x is an unknown.

(a) The highest power of x is 2.

(b) For example, 5x²– 6x + 3 is a quadratic expression.

Example 1

State whether each of the following is a quadratic expression in one unknown.

(a) x² – 5x + 3

(b) 8p² + 10

(d) 2x² + 4y + 14

(e)

2 p + \frac{1}{p} + 6

(f) y³ – 3y + 1

Solution:

(a) Yes. A quadratic expression in one unknown.

(b) Yes. A quadratic expression in one unknown.

(c) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

(d) Not a quadratic expression in one unknown. There are 2 unknowns, x and y in the quadratic expression.

(e) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

\frac{1}{p} = p^{- 1}

(f) Not a quadratic expression in one unknown. The highest power of the unknown x is not 2.

2. A quadratic expression can be formed by multiplying two linear expressions.

(2x + 3)(x - 3) = 2x² – 3x – 9

Example 2

Multiply the following pairs of linear expressions.

(a) (4x + 3)(x – 2)

(b) (y – 6)²

Solution:

(a) (4x + 3)(x – 2)

= (4x)(x) + (4x)(-2) +(3)(x) + (3)(-2)

= 4x² – 8x + 3x – 6

= 4x² – 5x – 6

(b) (y – 6)²

= (y – 6)(y – 6)

= (y)(y) + (y)(-6) + (-6)(y) + (-6)(-6)

= y² -6y – 6y + 36

= y² - 12y + 36

(c) 2x (x – 5)

= 2x(x) + 2x(-5)

= 2x² – 10x

Quadratic Equations Long Questions (Question 1 – 4)

Posted on April 23, 2020 by user

Question 1:

Solve the quadratic equation, (y + 3)(y – 4) = 30

Solution:

(y + 3)(y – 4) = 30

y² – 4y + 3y– 12 = 30

y² – y – 12 – 30 = 0

y² – y – 42 = 0

(y + 6)(y – 7) = 0

y + 6 = 0, y = –6

y – 7 = 0

y = 7

Question 2:

Solve the quadratic equation, 5x² = 3( x – 2) + 8

Solution:

5x² = 3x – 6 + 8

5x² – 3x – 2 = 0

(5x + 2)(x – 1) = 0

5x + 2 = 0, x

- \frac{2}{5}

x – 1 = 0

x = 1

Question 3:

Solve the quadratic equation

\frac{2 p^{2} - 15}{p} = 7

Solution:

\frac{2 p^{2} - 15}{p} = 7

2p² – 15 = 7p

2p² –7p – 15 = 0

(2p + 3)(p – 5) = 0

2p + 3 = 0, p =

- \frac{3}{2}

p – 5 = 0

p = 5

Question 4:

Solve the quadratic equation

y (y - \frac{9}{2}) = \frac{5}{2}

Solution:

\begin{array}{l} y (y - \frac{9}{2}) = \frac{5}{2} \\ y^{2} - \frac{9 y}{2} = \frac{5}{2} \end{array}

( ×2), 2y² – 9y= 5

2y² – 9y – 5 = 0

(2y + 1)(y – 5) = 0

2y + 1 = 0, y = – ½

y – 5 = 0

y = 5