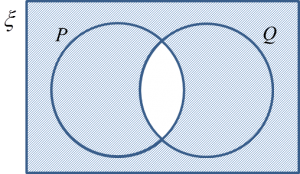
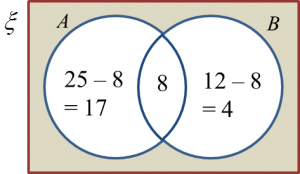Question 9 (3 marks):
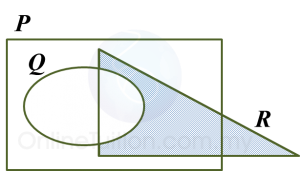
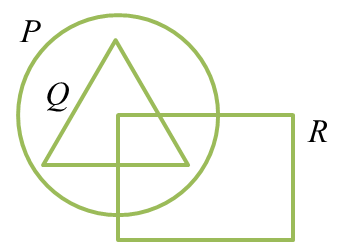
The Venn diagram in the answer space shows set P, set Q and set R such that the universal set ξ = P U Q U R.
On the diagram in the answer space, shade the set
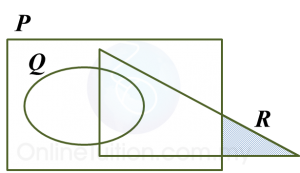
(a) P’,
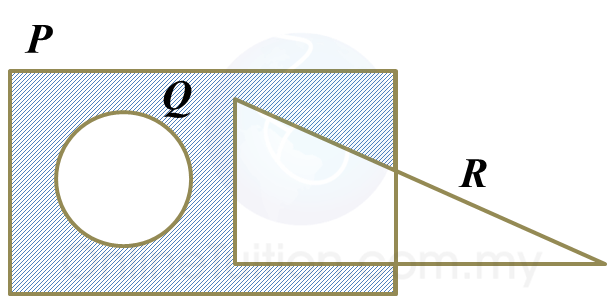
(b) (P ∩ Q) U R
Answer:

Solution:
(a)

(b)

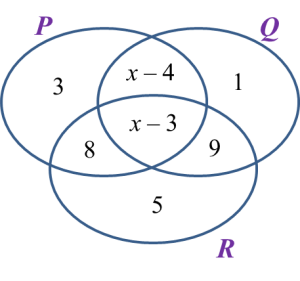
The Venn diagram in the answer space shows set P, set Q and set R such that the universal set ξ = P U Q U R.
On the diagram in the answer space, shade the set
(a) P’,
(b) (P ∩ Q) U R
Answer:

Solution:
(a)

(b)

Question 10 (3 marks):
(a) It is given that set E = {perfect square numbers} and set F = {9, 16, 25}.
Complete the Venn diagram in the answer space to show the relationship between set E and set F.
Answer:

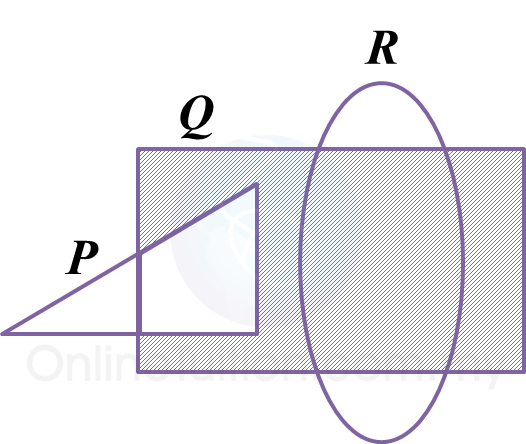
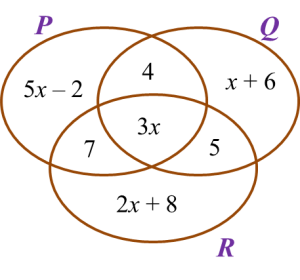
(b) The Venn diagram in Diagram 1 shows the sets X, set Y and set Z.
The universal set, ξ = X U Y U Z.
 Diagram 1
Diagram 1
State the relationship represented by the shaded region between sets X, set Y and set Z.
Solution:
(a)

(b)

Hence, relationship represented by the shaded region between sets X, set Y and set Z are (X ∩ Y) ∪ Z.
(a) It is given that set E = {perfect square numbers} and set F = {9, 16, 25}.
Complete the Venn diagram in the answer space to show the relationship between set E and set F.
Answer:

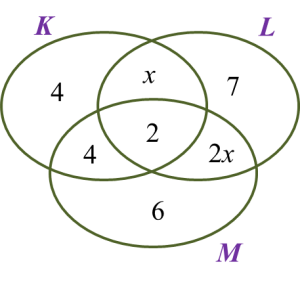
(b) The Venn diagram in Diagram 1 shows the sets X, set Y and set Z.
The universal set, ξ = X U Y U Z.
 Diagram 1
Diagram 1State the relationship represented by the shaded region between sets X, set Y and set Z.
Solution:
(a)

(b)

Hence, relationship represented by the shaded region between sets X, set Y and set Z are (X ∩ Y) ∪ Z.