Question 11 (5 marks):
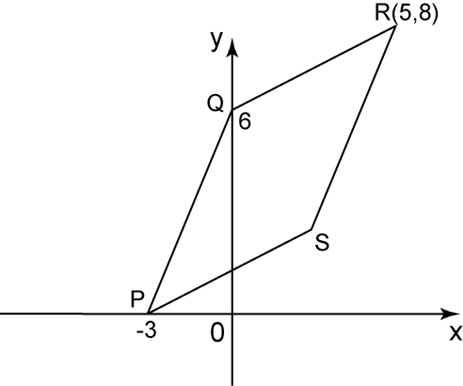
Diagram 4 shows a parallelogram drawn on a Cartesian plane which represents the locations of Rahman's house, a cinema, a school and a shop.

It is given that the scale is 1 unit : 1 km.
(a) Calculate the distance, in km, between Rahman's house and the school.
(b) Find the equation of the straight line that links the school to the cinema.
Solution:
(a)
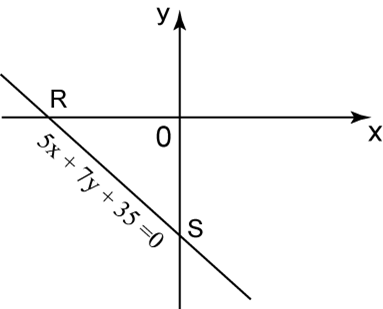
2y = 3x + 15
When y = 0
3x + 15 = 0
3x = –15
x = –5
Rahman's house = (–5, 0)
School = (3, 0)
Distance, between Rahman's house and the school
= 3 – (– 5)
= 8 units
= 8 km
(b)
2y=3x+15y=32x+152Thus m=32At point (3, 0), y1=mx1+c0=32(3)+c92+c=0c=−92Thus, the linear equation isy=32x−922y=3x−9
Diagram 4 shows a parallelogram drawn on a Cartesian plane which represents the locations of Rahman's house, a cinema, a school and a shop.

It is given that the scale is 1 unit : 1 km.
(a) Calculate the distance, in km, between Rahman's house and the school.
(b) Find the equation of the straight line that links the school to the cinema.
Solution:
(a)
2y = 3x + 15
When y = 0
3x + 15 = 0
3x = –15
x = –5
Rahman's house = (–5, 0)
School = (3, 0)
Distance, between Rahman's house and the school
= 3 – (– 5)
= 8 units
= 8 km
(b)
2y=3x+15y=32x+152Thus m=32At point (3, 0), y1=mx1+c0=32(3)+c92+c=0c=−92Thus, the linear equation isy=32x−922y=3x−9
Question 12 (6 marks):
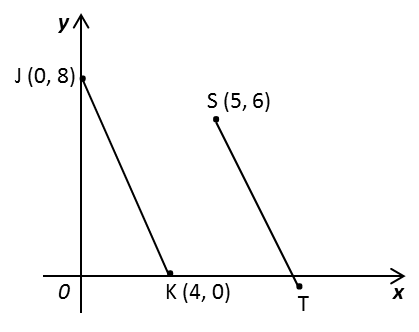
Diagram 6 shows two parallel straight lines, JK and LM, drawn on a Cartesian plane.
The straight line KM is parallel to the x-axis.
 Diagram 6
Diagram 6
Find
(a) the equation of the straight line KM,
(b) the equation of the straight line LM,
(c) the value of k.
Solution:
(a)
The equation of the straight line KM is y = 3
(b)
Given, equation of JK:2y=4x+3y=2x+32Thus, mJK=2mLM=mJK=2y=mx+cAt M(5, 3)3=2(5)+c3=10+cc=−7∴
(c)
Diagram 6 shows two parallel straight lines, JK and LM, drawn on a Cartesian plane.
The straight line KM is parallel to the x-axis.
 Diagram 6
Diagram 6Find
(a) the equation of the straight line KM,
(b) the equation of the straight line LM,
(c) the value of k.
Solution:
(a)
The equation of the straight line KM is y = 3
(b)
Given, equation of JK:2y=4x+3y=2x+32Thus, mJK=2mLM=mJK=2y=mx+cAt M(5, 3)3=2(5)+c3=10+cc=−7∴
(c)
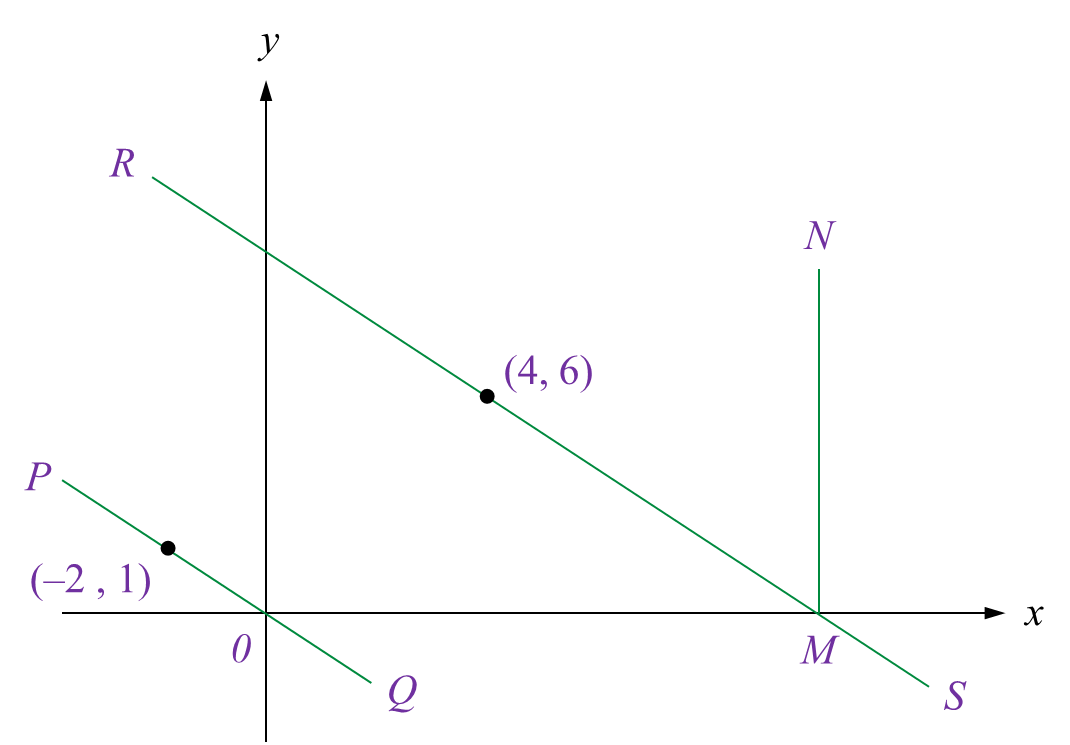 Diagram 6
Diagram 6